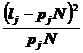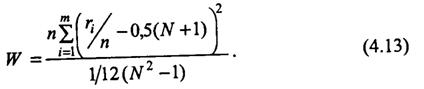
Числитель выражения (4.13) есть умноженная на п сумма квадратов отклонений средних рангов для каждой случайной величины Хi от средне­го ранга по всей последовательности; средний ранг рассчитывается по формуле

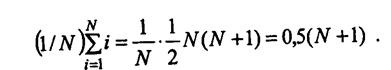
Знаменатель выражения (4.13) — средний квадрат отклонения от среднего ранга всех элементов последовательности. Если все Хi имеют один и тот же закон распределения, то W принимает малые значения, при разных законах распределения Хi, (т. е. при отсутствии стационарности) W принимает большие значения.

При совпадении законов распределения Хi статистика W(N-l)/N имеет χ2- распределение с числом степеней свободы v=m-1. Поэтому для про­верки гипотезы о стационарности потока (одинаковости распределений слу­чайных величин Xi) необходимо:

·  задаться уровнем значимости α (обычно 0,05 или 0,01);

·  в таблицах χ2 — распределения [9,11] найти квантиль распределения порядка 1-α, при v степенях свободы ;

·  если , то гипотезу о стационарности следует отклонить, в противном случае может быть сделан вывод о соответствии результатов наблюдений предположению о стационарности потока.

1.5.4.2. Проверка отсутствия последействия

В случае отсутствия последействия случайные величины Х1,...,Хm явля­ются независимыми. Проверку независимости случайных величин Х1,...,Хm можно осуществить с помощью критерия серий [7,9].

Для вычисления значения статистики S критерия серий необходимо:

объединить n реализаций случайных величин Х1, i=1,...,m в одну после­довательность с тп элементами и найти ее медиану М;

построить модифицированную последовательность, заменяя xi(j) на

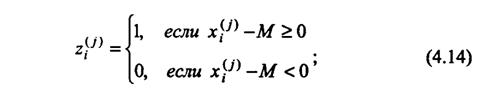
рассчитать число серий S в модифицированной последовательности (серия — это последовательность из одинаковых символов). При четном N число единиц и нулей в модифицированной последовательности будет одинаковым.

При независимости одинаково распределенных величин Хi, i=1,...,m (при стационарности потока) на каждом месте в модифицированной последовательности может с равной вероятностью стоять 1 или 0, а всего имеет место СNk равновероятных вариантов (реализации) этой пос­ледовательности, где k — число единиц в модифицированной последова­тельности. Эти варианты можно перебрать (СNk — это число сочетаний из N по k, или число вариантов расположения k единиц в последовательности длиною N), рассчитать для каждого число серий S и построить функцию распределения числа серий. Малые и большие значения величины 5 свидетельствуют о наличии зависимости между величинами Xi, (о наличии последействия в потоке),

·  задаться уровнем значимости α (0,05 или 0,01);

·  по таблицам распределения числа серий [9,11] при заданных N,k (k - число единиц в модифицированной последовательности) и а найти ниж­нюю и верхнюю границы критической области;

·  если рассчитанное значение статистики S не удовлетворяет неравен­ству <S<, то гипотеза о независимости отклоняется; в противном случае делается вывод о соответствии результатов наблюдений предположению об отсутствии последействия в потоке.

1.5.4.3. Проверка гипотезы о пуассоновском распределении числа сообщений

Если тесты (см. пп. 1.5.4.1 и 1.5.4.2) дали положительный резуль­тат (т. е. гипотезы о стационарности и отсутствии последействия не от­клонены), то следует выполнить проверку гипотезы о том, что закон распределения числа сообщений (т. е. величин Хi, i=1,...,m) пуассоновский. Для этого можно воспользоваться критерием согласия Пирсона χ2[9].

Выборка наблюдений содержит пт элементов xi(j), j=1,...,n, i=1,...,m. Каждое наблюдение xi(j) — число сообщений в течение интервала Δt = 1ч в j-е сутки наблюдений.

По выборке находим оценку параметра α закона распределения Пуас­сона:

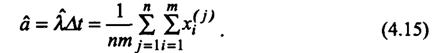
Для вычисления статистики критерия необходимо:

·  разбить диапазон значений xi(j) на k≥6 классов так, чтобы число наблюде­ний пμ каждого класса было бы не менее 5ч6;

·  рассчитать теоретические вероятности рμ попадания в каждый класс значений:

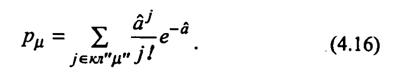
Суммирование в выражении (4.16) осуществляется по значениям числа сообщений, принадлежащих μ-ому классу. Для последнего (k-го) класса

а для первого класса суммирование начинается c j=0;

·  найти значение статистики

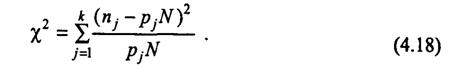
Эта статистика имеет χ2 - распределение с числом степеней свободы v=k-1-r, где r - число параметров закона распределения, оценки которых получены по выборке и использованы при вычислении χ2 (для зако­на распределения Пуассона r=1). Статистика χ2 принимает большие значения, когда экспериментальные данные не соответствуют гипотезе о пуассоновском распределении. В процессе проверки гипотезы необ­ходимо:

o  задаться уровнем значимости a (0,05 или 0,01);

o  по таблице из [9,11] найти квантиль χ2-распределения порядка 1-α при v степенях свободы ();

o  если рассчитанное значение , то гипотеза о том, что закон распределения пуассоновский, отклоняется. В противном случае делается вывод о том, что имеющиеся данные не противоречат предположению о пуассоновском распределении числа событий.

1.5.4.4. Выбор модели потока сообщений о погрузке и выгрузке вагонов на станции

В табл.1.1 приведены данные о числе сообщений о погрузке-выгрузке вагонов, поступавших в течение каждого часа с 8 до 18 ч. на протяжении трех суток [7].

На основе приведенных в табл.4.1 данных дадим обоснования для вы­бора простейшей модели потока сообщений.

Проверка стационарного потока. Используем критерий Крускала-Уоллиса (см. п. 1.5.4.1). В табл. 1.1 приведены ранги наблюдений и суммарные ранги (ri, i=1,10) по 10 часовым интервалам1). В данном примере п=3, т=10, N=nm=30:

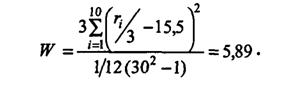
Зададимся уровнем значимости α=0,05. Из таблицы χ2— распределе­ния при v=m-1=9 находим .

Так как , то основания для отклонения гипотезы о совпадении законов распределения нет. Поток сообщений можно считать стационарным.

Проверка отсутствия последействия. Используем критерий серии (см. п. 1.5.4.2). Медиана последовательности из N=30 выборочных значений табл.1.1 М=4.

Модифицированная последовательность, полученная по правилу (4.14), приведена табл.1.1. Здесь k=18 (число единиц), N-k=12 (число нулей).

Зададимся уровнем значимости α = 0,05. По таблицам из [9] находим ; .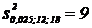

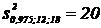По модифицированной последовательности из табл.1.1 рассчиты­ваем число серий S=17. Так как значение S= 17 оказывается в промежутке между и , то делаем вывод о независи­мости чисел сообщений на последовательных непересекающихся интер­валах

1)В данных табл. 1.1 выборка содержит много совпадающих элементов. В том случае в знаменателе формулы (4.13) для статистики Крускала-Уоллиса следует ввести поправку [9].

времени, и, следовательно, о соответствии результатов наблюдений предположению об отсутствии последействия в потоке.

Таблица 1.1.

Данные о числе сообщений о погрузке-выгрузке вагонов

Проверка гипотезы о пуассоновском распределении числа сообщений. Найдем оценку параметра закона распределения Пуассона. Так как в за­коне Пуассона α — это математическое ожидание числа событий (сообще­ний) на заданном интервале (в данном случае — в течение 1ч), то согласно методу моментов [9] имеем:

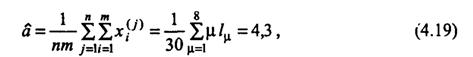
где lμ — число раз, когда в течение 1ч на станцию поступало μ сообще­ний.

Ниже приведена сгруппированная выборка:

Отметим, что в данном случае из-за недостаточного объема выборки (N=30) не удается обеспечить условие k≥6 при lμ≥5ч6. Поэтому распреде­ление статистики лишь приближенно следует закону χ2.

Расчет значения χ2 показан в табл. 1.2.

Таблица 1.2.

Расчет значения χ2

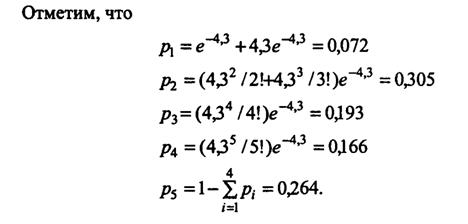
Полученное значение χ2=0,438 является реализацией случайной вели­чины, подчиненной χ2 — распределению с v=5-1-1=3.

Приняв a=0,05, находим в таблицах из [9] .

Так как 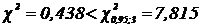, то нет оснований для отклонения гипотезы о пуассоновском распределении числа сообщений о погрузке и выгрузке вагонов, поступающих на станцию в течении 1ч.

Проведенные исследования позволяют сделать вывод о возможности использования модели простейшего потока.

1.6. Процедуры обоснования решений при проектировании информационных систем

1.6.1. Постановка задачи выбора варианта решения

Проектирование — это выбор лучшего варианта построения системы: лучшей программно-технической платформы, СУБД, размещения комплек­са технических средств, технологии передачи данных, топологии сети и т. д.

Выбор — это почти всегда компромисс между противоречивыми тре­бованиями, стремлением к широким возможностям создаваемой системы и низкой стоимостью.

Формально задача выбора лучшего варианта создаваемой системы (технологии, элемента системы) ставится следующим образом. Имеется^ вариантов решения, каждый из которых может быть оценен по k различным характеристикам. Все варианты приемлемы, т. е. среди них отсутствуют такие, которые могли бы быть исключены из рассмотре­ния по ограничениям, жестко накладываемым на какие-либо показате­ли. Например, если имеются ограничения на стоимость, несоответ­ствующие этому условию варианты исключаются из дальнейшего рас­смотрения. Из N вариантов надо выбрать лучший по совокупности характеристик.

Для обоснования выбора лучшего варианта может быть использована процедура, основанная на экспертных оценках и включающая следующие действия:

составление полного перечня характеристик (свойств, показателей), по которым следует производить выбор;

оценку важности каждой характеристики на основе процедур экспер­тного оценивания;

оценку степени обладания каждым вариантом решения, представлен­ным для выбора, каждым из рассматриваемых свойств;

оценку коэффициентов важности (предпочтительности) каждого ва­рианта и выявления варианта с наибольшим значением коэффициента важности.

1.6.2. Составление полного перечня характеристик (свойств, показателей)

При решении этой проблемы важно, чтобы были учтены все свойства, важные для принятия решений.

Один из возможных способов составления перечня характеристик зак­лючается в сборе и обработке мнений экспертов [7]. При этом каждому эксперту предлагается составить список характеристик (свойств, показа­телей), по которым следует осуществлять выбор варианта системы (тех­нологии и т. п.). Списки, представленные разными экспертами, объединя­ются. Объединенный список подвергается анализу, при котором выявля­ются отношения между каждой парой элементов списка. Эти отношения могут быть следующими:

тождественность — обладание первым свойством означает облада­ние и вторым, и наоборот. Например, свойства "безопасность данных" и "защита данных от несанкционированного доступа" являются тождественными;

подчиненность — второе свойство подчинено первому, если обладание первым свойством означает и обладание вторым, но не наоборот. Напри­мер, свойство "достоверность данных" подчинено свойству "качество дан­ных", так как "достоверность" является одной из составляющих понятия "качество данных";

независимость — обладание одним свойством никак не отражается на степени обладания другим. Например, независимы свойства "нали­чие доступной документации" и "скорость выполнения операции" и т. д.

Определение окончательного перечня характеристик осуществляется: исключением одного из каждой пары тождественных свойств; при наличии множества свойств, подчиненных одному (первому), из списка удаляются первое свойство либо множество подчиненных ему свойств.

В результате реализации этой процедуры в списке характеристик остаётся только множество независимых свойств вариантов выбора.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4