Сжатие двухслойного кусочно-неоднородного материала
Сжатие двухслойного кусочно-неоднородного материала
Екатеринбург, Россия
Для разработки процесса пакетной прокатки необходимо знание, по крайней мере на качественном уровне, поведения каждого материального слоя в пакете, т. е. их напряженно - деформированное состояние, при совместном упруго-пластическом деформировании. Это позволит определить принципиальную возможность осуществления процесса, подобрать материалы и оценить качество пакета после прокатки. В данной работе излагается решение задачи об определении напряжений и деформаций в двухслойном пакете при его сжатии при условии аддитивности деформаций. Полученные результаты, по крайней мере в первом приближении, могут ответить на поставленные выше вопросы.
1.Постановка задачи. Рассмотрим прямоугольный параллелепипед, состоящий из двух одинаковых по размерам слоев 1 и 2. Высота параллелепипеда равна ![]() (
(![]() - толщина слоев), а ширина и глубина имеют единичный размер (площадь
- толщина слоев), а ширина и глубина имеют единичный размер (площадь ![]() основания равна единице). Параллелепипед расположен между двух массивных жестких плит. Нижняя плита неподвижна, а верхняя перемещается вниз на величину
основания равна единице). Параллелепипед расположен между двух массивных жестких плит. Нижняя плита неподвижна, а верхняя перемещается вниз на величину ![]() , сжимая параллелепипед. При этом граница слоев смещается на величину
, сжимая параллелепипед. При этом граница слоев смещается на величину ![]() (рис.1). Свойства слоев различны.
(рис.1). Свойства слоев различны.
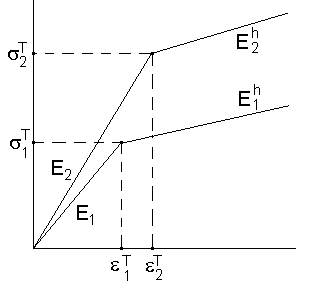
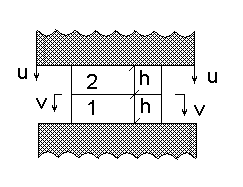
Рис. 1 | Рис. 2 |
Первый слой имеет модуль Юнга ![]() , модуль упрочнения
, модуль упрочнения ![]() и предел текучести
и предел текучести ![]() . Второй слой имеет модуль Юнга
. Второй слой имеет модуль Юнга ![]() , модуль упрочнения
, модуль упрочнения ![]() и предел текучести
и предел текучести ![]() . Для определенности полагаем, что
. Для определенности полагаем, что 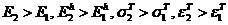 (рис.2) (
(рис.2) (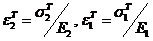 - деформации на пределе текучести). Требуется найти напряжения и деформации слоев в зависимости от смещения
- деформации на пределе текучести). Требуется найти напряжения и деформации слоев в зависимости от смещения ![]() верхней плиты.
верхней плиты.
2. Слои в упругом состоянии. Пусть перемещение ![]() таково, что материал обоих слоев находится в упругом состоянии. В этом случае состояние системы описывает потенциальная функция
таково, что материал обоих слоев находится в упругом состоянии. В этом случае состояние системы описывает потенциальная функция
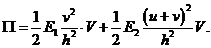 (1) Здесь первое слагаемое – потенциальная энергия упругих деформаций первого слоя, второе слагаемое – потенциальная энергия упругих деформаций второго слоя,
(1) Здесь первое слагаемое – потенциальная энергия упругих деформаций первого слоя, второе слагаемое – потенциальная энергия упругих деформаций второго слоя, ![]() - деформация в первом слое,
- деформация в первом слое, ![]() - деформация во втором слое,
- деформация во втором слое, 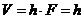 - объемы слоев. Используя функцию (1) найдем уравнение равновесия [1]
- объемы слоев. Используя функцию (1) найдем уравнение равновесия [1]
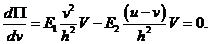 Отсюда в положении равновесия
Отсюда в положении равновесия
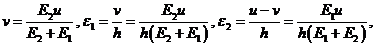
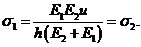 Ясно, что
Ясно, что ![]()
Определим теперь величину перемещения ![]() , после достижения которой материал первого слоя перейдет в состояние пластичности. Имеем
, после достижения которой материал первого слоя перейдет в состояние пластичности. Имеем
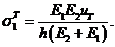
Отсюда
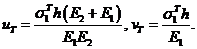
3. Упругопластическое состояние первого слоя. Пусть перемещение ![]() . В этом случае состояние системы описывает потенциальная функция [1]
. В этом случае состояние системы описывает потенциальная функция [1]
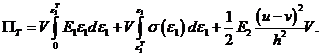 (2) Здесь первые два слагаемых являются полной энергией деформаций первого слоя после перехода его в состояние пластичности. Используя функцию (2), найдем уравнение равновесия [1]
(2) Здесь первые два слагаемых являются полной энергией деформаций первого слоя после перехода его в состояние пластичности. Используя функцию (2), найдем уравнение равновесия [1]
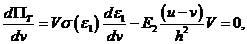 где
где ![]() Тогда уравнение равновесия принимает вид
Тогда уравнение равновесия принимает вид
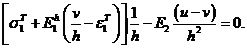 Отсюда
Отсюда
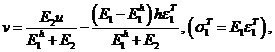
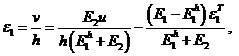

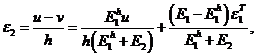
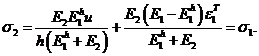
Рассмотрим предельный случай, когда ![]() Имеем
Имеем ![]() Таким образом, при возрастании перемещения
Таким образом, при возрастании перемещения ![]() напряжения в системе остаются постоянными, деформация второго слоя также постоянна, а деформация первого слоя возрастает пропорционально перемещению
напряжения в системе остаются постоянными, деформация второго слоя также постоянна, а деформация первого слоя возрастает пропорционально перемещению ![]() .
.
4. Упругопластическое состояние первого и второго слоев. Рассуждения, приведенные выше, показывают, что достигнуть упругопластического состояния во втором слое возможно лишь при достаточно большой величине модуля ![]() . Пусть это условие выполняется. Найдем тогда значение перемещения
. Пусть это условие выполняется. Найдем тогда значение перемещения ![]() , при котором второй слой перейдет в состояние пластичности. Имеем
, при котором второй слой перейдет в состояние пластичности. Имеем
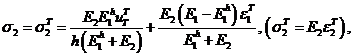
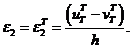 Отсюда
Отсюда
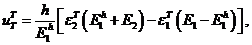
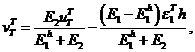
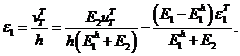 Отметим, что при
Отметим, что при ![]() получаем
получаем ![]() и
и ![]() . Это и означает невозможность достижения вторым слоем пластического состояния.
. Это и означает невозможность достижения вторым слоем пластического состояния.
Снова запишем потенциальную функцию системы [1]
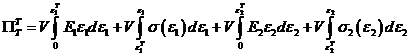 . (3) Здесь
. (3) Здесь ![]() Используя функцию (3), найдем уравнение равновесия [1]
Используя функцию (3), найдем уравнение равновесия [1]
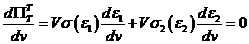 или
или
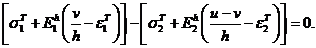 Отсюда
Отсюда
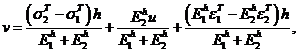
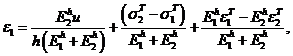
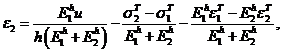
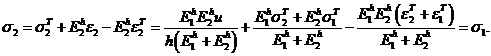
Заключение
1. В предположении об аддитивности деформации получены выражения для определения напряжений и деформаций при сжатии двух слоев различных по свойствам материалов на упругой и упругопластической стадиях деформирования.
2. Установлено, что оба слоя могут перейти в пластичность только при достаточной близости свойств.
Литература
1. , Миронов разупрочнение материала в элементах конструкций. Екатеринбург: Изд-во УрО РАН, 1995.191с.



