Н. Е. ЧИЖКОВА
Снежинская государственная физико-техническая академия
ИзЭнтропическое автомодельное
сжатие газа
Повышенный интерес к режимам изэнтропического сжатия обусловлен поиском путей осуществления воспламенения термоядерных процессов с помощью какой-либо из схем инерциального термоядерного синтеза. Кроме того, такие решения представляют особую ценность, как тестовые для проверки применимости численных методов решения уравнений газодинамики к течениям с повышенной степенью кумуляции.
Точное решение задачи об изэнтропическом сжатии однородного идеального газа впервые было получено [1] для плоских течений. Возможность обобщения таких решений для случая сферической и цилиндрической симметрий была показана
и [2]. [3] и [4] расширили такие исследования, обратив внимание на их энергетические показатели.
В качестве автомодельной переменной используется ![]() , где
, где ![]() – начальная скорость звука,
– начальная скорость звука, ![]() – расстояние до места фокусировки, время
– расстояние до места фокусировки, время 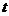 отсчитывается от момента фокусировки. Как в [2] используется представление уравнений газодинамики через инварианты Римана
отсчитывается от момента фокусировки. Как в [2] используется представление уравнений газодинамики через инварианты Римана ![]() и
и ![]() , где
, где ![]() и
и ![]() – скорость вещества и звука, можно получить уравнения адиабатического движения для идеального газа. Для исследований удобны переменные
– скорость вещества и звука, можно получить уравнения адиабатического движения для идеального газа. Для исследований удобны переменные ![]() ,
, ![]() . На рисунке на плоскости
. На рисунке на плоскости ![]() представлены изоклины нулей и бесконечностей, некоторые интегральные кривые и ударная адиабата, соответствующая отраженной от центра ударной волне.
представлены изоклины нулей и бесконечностей, некоторые интегральные кривые и ударная адиабата, соответствующая отраженной от центра ударной волне.
Исходному покоящемуся состоянию вещества соответствует точка N. Интерес представляют интегральные кривые, исходящие из точки N, вдоль которых ![]() монотонно стремится к нулю. Качественное исследование интегральных кривых осуществляется путем рассмотрения изменения знака наклонов
монотонно стремится к нулю. Качественное исследование интегральных кривых осуществляется путем рассмотрения изменения знака наклонов ![]() , выяснения характера особых точек и изучения поведения интегральных кривых в окрестности особых точек.
, выяснения характера особых точек и изучения поведения интегральных кривых в окрестности особых точек.
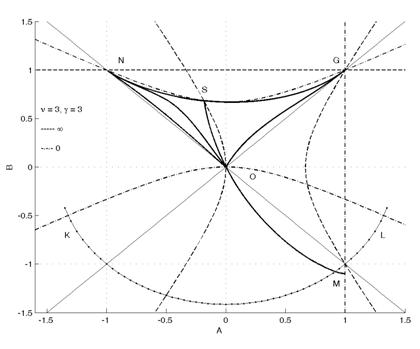
Фокусировке вещества в точку отвечает особое решение, приходящее в седло ![]() . Семейство интегральных кривых, проходящих через дикритический узел
. Семейство интегральных кривых, проходящих через дикритический узел ![]() , заполняющих треугольник
, заполняющих треугольник ![]() и приходящих на ударную адиабату
и приходящих на ударную адиабату ![]() , отвечает двухэнтропийным сжатиям с ударным дожатием волной, отраженной от центра симметрии. Луч
, отвечает двухэнтропийным сжатиям с ударным дожатием волной, отраженной от центра симметрии. Луч ![]() соответствует покою. Решениям при
соответствует покою. Решениям при ![]() отвечают конечные сжатия, причем в момент фокусировки вещество однородно и движется с постоянной скоростью к центру. Это состояние является начальным для известной задачи [5]: после фокусировки от центра идет ударная волна, за которой вещество покоится.
отвечают конечные сжатия, причем в момент фокусировки вещество однородно и движется с постоянной скоростью к центру. Это состояние является начальным для известной задачи [5]: после фокусировки от центра идет ударная волна, за которой вещество покоится.
Работа выполнена по гранту Минобразования и Минатома РФ по научно-инновационному сотрудничеству.
Список литературы
1. , Неустановившиеся движения сплошной среды. М., Гостехиздат. 1955.
2. , , Прикладная математика и механика, том 42, вып. 3, Сферическая волна сжатия, М., Академия наук СССР. 1978.
3. , Прикладная математика и механика. Т.60. Вып.6. О неограниченной кумуляции при одномерном нестационарном сжатии идеального газа. М., Российская академия наук. 1996.
4. Kraiko A. N. and Tillyaeva N. I., High temperature, vol. 36, No. 1, Self-similar compression of ideal gas by a disk, cylindrical or spherical piston. M. Nauka. 1998.
5. , Методы подобия и размерностей в механике. М, Наука. 1987.



