Таб3.3 элементы матрицы.

3.4. Расчет коэффициента эффективности.

K=∑kijп/∑kijд

Где kijп - элемент матрицы Александера, находящийся на пересечении i-ой строки и j-го столбца в матрице соответствия после внесения изменений в систему, а

kijд - элемент матрицы Александера, находящийся на пересечении i-ой строки и j-го столбца в матрице соответствия до внесения изменений в систему

Таким образом для нашей системы получаем коэффициент корреляции K=2/5=0.4

3.5. Структурная схема системы.

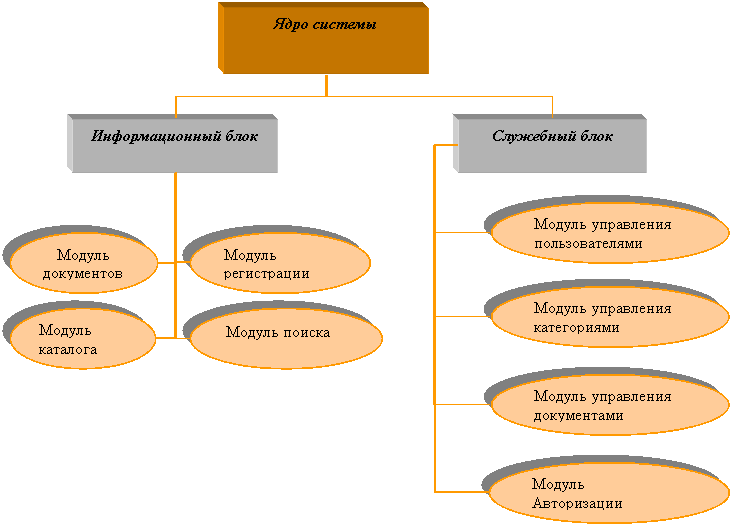
Рис. 3.5Структурная схема информационной системы

Ядро системы – центральный блок системы, осуществляющий связь между всеми компонентами системы.

Информационный блок – предоставляет интерфейс пользователю для доступа к информации, отвечает за хранение, каталогизацию информации и поиск по ней.

Служебный блок – предназначен для администрирования системы, внесения структурных изменений, работы с карточками пользователей, контентом системы.

На основании описания состава и особенностей всех перечисленных выше ступеней менеджмента проекта ИС формируется сетевой график проектирования ИС.

4.1. Дивергенция

Дивергенция означает расширение границ проектного этапа на самых ранних стадиях проектирования (предпроектного обследования) с целью обеспечения обширного пространства для поиска решений.

На ступени дивергенции автором принимались во внимание в качестве ключевых следующие особенности принятия решений:

·  задачи поиска неустойчивы и условны;

·  границы поиска также неустойчивы и неопределенны;

·  принимается во внимание все, что может иметь отношение к решению задач, а оценки откладываются на будущее;

·  главной стартовой точкой ступени дивергенции является техническое задание (ТЗ) заказчика, но предполагается, что задание до конца не сформировано и может быть подвержено изменениям (или только создаваться на основе Технических предложений);

·  проверка стабильных и нестабильных точек, устойчивости предлагаемых решений под воздействием изменения внешних обстоятельств;

·  главное в дивергенции – свободный поиск с синхронным отслеживанием реакции заказчика или взаимодействующих технических средств на предлагаемые пути решений.

Дивергенция начинается в предпроектной стадии и продолжается на этапах разработки технического задания, моделирования и, отчасти, эскизного проектирования.

На данной стадии был произведен анализ технического задания, исследована предметная область, намечены общие границы проекта, рассмотрены различные варианты путей разработки проекта. Проведен анализ существующих систем. Обоснован выбор программной платформы и технологии. Проведен анализ материала, наполняющего информационную систему. Сформулированы основные направления развития системы.

В перечень решенных задач на стадии дивергенции вошли следующие:

·  Выбор платформы для проектирования. В связи с целью проекта выбор был остановлен на операционной системе Windows 98, СУБД MS SQL Server 4.0.12 и языке разработке интерфейса PHP.

·  Создание нескольких уровней пользователей для обеспечения безопасности и целостности данных.

·  Выбор атрибутов поиска (по названию).

4.2. Трансформация.

На ступени трансформации с опорой на результаты дивергенции сформированы в необратимом виде основные принципы и концепции проекта. В принципе могут решаться также задачи оптимизации, но, как это показано ниже, в настоящем проекте необходимости введения оптимизационных решений не ощущалось, так как требуемые показатели ИС (производительность, надежность и другие) были получены сразу же при реализации первой траектории расчетов ИС. По этой же причине не возникли ситуации, требующие введения интраверсии на переходах от дивергенции к трансформации и от трансформации к конференции.

На ступени трансформации в проекте:

·  на результаты дивергенции накладывается принципиальная схема;

·  формируются, взаимно увязываются и свободно перемещаются в проектном пространстве подцели, отвечающие главной цели проекта;

·  осуществляется переход от сложной комплексной размытой многофакторной задачи к набору последовательно решаемых простых однозначных и ясно сформулированных задач с четко определенными границами и начальными условиями;

·  окончательно формируются ТЗ, технические требования к проектируемому изделию (ТТ) и технические условия его эксплуатации (ТУ).

Трансформация завершает эскизное проектирование и, тем более, делает незыблемым ТЗ на проект (за исключением форс-мажорных обстоятельств, если это оговорено в договоре на проект). Менеджмент проектирования определен.

На этой стадии все ошибки системы устранены, система готова к использованию. При доработке выявляются новые цели или дорабатываются (расширяются) старые. Дорабатывается (вносятся изменения) в техническое задание, технические условия и технические требования. Также здесь происходит наполнение информационной системы.

В перечень решенных задач на стадии трансформации вошли следующие:

Рассчитана производительность системы.

·  Спроектирована база данных.

·  Сделан интерфейс системы, представляющий из себя html-станицы для взаимодействия с базой данных.

·  Выполнено первоначальное наполнение базы данных литературой, а также в окружение ядра ИС выполнено наполнение ссылками интернет-адресов.

·  Осуществлено тестирование системы.

4.3. Конвергенция.

Конвергенция является последней ступенью проектирования. Ступень конвергенции вступает в действие только тогда, когда задачи корректно и окончательно определены, все переменные величины найдены или ограничены, подцели установлены и окончательно закреплены в проектном пространстве. Следовательно, конвергенция представляет набор описываемых алгоритмом последовательных стандартизуемых действий и операций, приводящих к появлению проектируемого изделия, его проверке и разработке проектной документации передаваемой заказчику (включая акты приемо-сдаточных испытаний, каталожное описание (КО) изделия, различные инструкции и демоверсии).

Конвергенция относится в основном к этапу рабочего проектирования.

На этой заключительной стадии разрабатываются приложения к информационной системе. Здесь все описание системы полностью готово, разработаны инструкции пользователя всем уровням доступа к системе, инструкции по установке и ликвидации. Проект считается полностью завершенным.

В перечень решенных задач на стадии конвергенции вошли следующие:

·  Разработка инструкций пользователям по различным уровням доступа (гость, зарегистрированный пользователь, администратор).

·  Разработка инструкции по установке и ликвидации системы.

·  Разработка технических требований к аппаратному и программному обеспечению для полноценной работы системы.

·  Составление проектной документации, в том числе всех приложений (библиографический список, ресурсная область, листинг программы, акт внедрения).

·  Подписание акта внедрения и внедрение информационной системы в МГДД(Ю)Т.

·  Подготовка листов графики для наглядности системы.

выполняемые в логичной последовательности этапы работ позволяют планировать сроки завершения всех работ и соответствующие затраты.

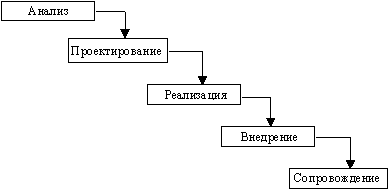
Рис.5.2.1 Каскадная схема разработки ПО

Однако, в процессе использования этого подхода обнаружился ряд его недостатков, вызванных прежде всего тем, что реальный процесс создания ПО никогда полностью не укладывался в такую жесткую схему. В процессе создания ПО постоянно возникала потребность в возврате к предыдущим этапам и уточнении или пересмотре ранее принятых решений. В результате реальный процесс создания ПО принимал следующий вид

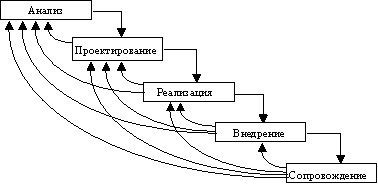
Рис. 5.2.2 Реальный процесс разработки ПО по каскадной схеме

5.3. Расчет полного жизненного цикла системы.

На ступени дивергенции рассчитывается полный жизненный цикл ИС, если он не задан в ТЗ. В настоящем проекте, по результатам аналитического обзора, представлен инвариантный набор процедур и методов такого расчета.

Как в сложных технических системах, так и в достаточно развитых ИС образования для оценки длительности полного жизненного цикла используют соответствующие математические модели. Традиционные модели оценки длительности жизненного цикла в своей основе имеют идеализированную схему (экспоненциальное распределение)

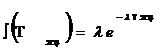
(1)

где — величина обратная средней длительности жизненного цикла.

Соотношению (1) соответствует пуассоновский поток событий.

Следует заметить, что эта закономерность наблюдается при эволюции технических систем повышенной сложности и стоимости уникальных систем и некоторых сложных и дорогостоящих технологий (например, технологий нефтехимии). Однако предположение о постоянстве параметра неприемлемо для широкого класса технических и особенно информационных систем, что обуславливает необходимость постулирования некоторых дополнительных предположений о вариации этого параметра.

Модификация универсальной зависимости (1) может осуществляться в двух направлениях, в одном из них можно считать, что параметр имеет детерминированную тенденцию изменения во времени. Более правдоподобно считать параметр случайной величиной с плотностью вероятности f().

Тогда

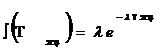
(2)

В простейшем случае вариация параметра имеет гамма-распределение

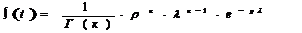
(3)

р — параметр масштаба,

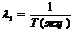
Тжц – средняя длительность жизненного цикла i-го типа технической (информационной) системы

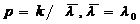Основным достоинством распределения (3) является его гибкость, поскольку оно содержит два подгоночных параметра.

Можно показать, что приняв получим

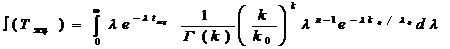
Определив интеграл, найдем плотность вероятности сложно-экспоненциального распределения

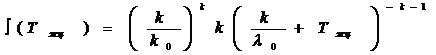
и интегральный закон распределения

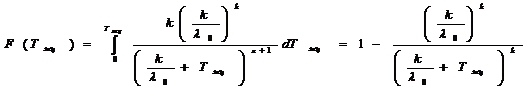
(4)

Это одна из модификаций распределения Парето. Его дисперсия превышает дисперсию того предельного экспоненциального распределения, к которому оно сходится при некоторых дополнительных условиях. Не останавливаясь здесь подробнее на довольно сложной оценке этих условий ограничимся утверждением, что в основном указанные условия достаточно полно соотносятся к специфике многомодульных информационных систем в образовании с выраженным достаточно устойчивым информационным ядром, отражающим предметную область изучения и нтернетм изменчивым многомодульным слабодетерминированным информационным окружением этого ядра.

Тогда, приняв для ИС образования такое развитие модели полного жизненного цикла ИС за генеральное, можно считать, что параметр интенсивности экспоненциального распределения может иметь тенденцию изменения во времени, которая может быть описана каким-либо уравнением тренда.

В этом случае интенсивность определяется двумя составляющими: константой a , не зависящей от длительности жизненного цикла сложной многомодульной технической или информационной системы, и слагаемым, экспоненциально растущим с «возрастом»,

(5)

Эта функция, постоянные которой а, b, и определяются статистическим путем на основе известных алгоритмов (например, методом трех сумм или методом трех точек), имеет горизонтальную асимптоту, равную а. Ее график стремится к асимптоте при Тдщ -> оо, но никогда ее не пересекает. Параметр b равен разности между ординатой кривой и асимптотой. Подставляя выражение (5) в исходную зависимость получим

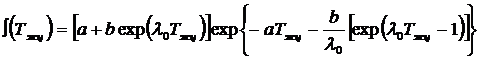
(6)

Это дифференциальный закон распределения Гомперца-Макегама. Его частным случаем при а = 0 (т. е. в случае представления уравнения тренда интенсивности простой экспонентой) является распределение Гомперца. Последнее при прогнозировании длительности жизненного цикла сложных технических и информационных систем представляет особый интерес, так как является стохастическим аналогом весьма известной кривой Гомперца и широко применяется при аппроксимации статистических данных процессов развития благодаря своей асимметричности.

Прогнозирования длительности жизненного цикла сложных технических и информационных систем методом Монте-Карло с использованием распределения Гомперца-Макегама.

Распределение Гомперца-Макегама в последнее время вызывает возрастающий интерес. Поэтому представляется целесообразным более подробно остановиться на моделирующем алгоритме, позволяющем получать случайные величины, распределенные по этому закону, при решении задач прогнозирования длительности полного жизненного цикла сложных технических систем методом Монте-Карло.

Предположим, что в определенный момент времени возникает группа контейнеров ИС. Такая группа называется системой. Допустим, что мы измеряем число актуальных контейнеров, через одинаковые промежутки времени «n». Число доживших до возраста «х» обозначают через l(x); разница между количеством доживших до возраста «х» и доживших до возраста «х+n» равна числу потерявших актуальность в возрастном интервале (х, х+n) и обозначается через d(x) или «d»; вероятность смерти ИС на интервале «n» ИС, доживших до возраста «х», обозначается через q(x) или «q» и определяется уравнением: q= d/l

Для вычисления ожидаемого времени полного жизненного цикла ИС, дожившего до возраста «х», которую обозначают е(х) или «е», используют промежуточные вычисления. Сначала определяют суммарное число лет L(х), проживаемых всей системой в интервале (х, х+n ): L(x) = n/2[l(x)+l(x+n)]

Данное соотношение строго справедливо, если функция l(x) является линейной на изучаемом интервале.

В реальности функция «l» нелинейна и поэтому, чтобы не допускать существенных ошибок в расчетах, интервал «n» необходимо выбирать не слишком большим, чтобы на нем функция «l» отличалась от прямой линии не более, чем на несколько процентов, если мы хотим, чтобы погрешность в расчетах также измерялась несколькими процентами.

Далее рассчитывают суммарное число лет Т(х), проживаемых когортой в возрасте «х» и старше (пока вся когорта не закончит свое существование): Т(х) = L(x)+…+L(w), где w это значение возраста, соответствующее началу последнего возрастного интервала.

Ожидаемая продолжительность предстоящей жизни для дожившего до возраста «х» определяется далее из соотношения: е(х) = Т(х)/l(x).

До настоящего времени формула Гомперца - Макегама остается наилучшей для описания жизненного цикла для самых различных систем. Теоретической основой формулы являлась предпосылка о том, что жизнеспособность системы «Х» с возрастом снижается в результате чисто вероятностного процесса, что дает основной закон: dX/dt = - a X,

где «а» – коэффициент пропорциональности.

Так как понятие жизнеспособности неопределенно, но эмпирически понятно, что жизнеспособность и вероятность смерти системы находятся в обратно пропорциональном соотношении, Гомперц принял в качестве меры жизнеспособности обратную ей величину m = 1/Х, где m – вероятность смерти. Тогда дифференциальное уравнение, описывающее динамику смертности, имеет следующий вид:

d[1/m(t)]/dt = - a[1/m(t)].

Интегрирование этого уравнения дает в результате знаменитую формулу Гомперца:

m(t) = Ro exp(a t).

После добавления Макегама константы «А» в правую часть этого уравнения оно приняло современный вид зависимости функционирования системы от возраста: m(t) = A + Ro exp(a t)

Здесь – «А» – константа, отражающая интенсивность функционирования системы от внешних условий, «Ro» – начальный уровень затухания и «a» – показатель, отражающий скорость нарастания потери актуальности с возрастом.

Принято представлять график экспоненты в полулогарифмических координатах, где она имеет вид прямой. Однако, аддитивная поправка Мейкема в правой части уравнения обусловливает отклонение от прямой линии зависимости ln(m) от t. Поскольку А является константой, получить в правой части уравнения чистую экспоненту можно, продифференцировав уравнение Гомперца-Мейкема. Тогда график в полулогарифмических координатах будет иметь вид прямой линии с тангенсом угла наклона к оси времени равным «а», которая пересекает ось ординат в точке Ro a. Поэтому значения Ro и а, соответственно характеризующие значение смертности в начальный момент времени t= 0 и темп старения, могут быть легко найдены из такого графика. Затем можно рассчитать значение поправки Макегама разност ежду наблюдаемым значением смертности и ее возрастной компонентой, описываемой экспонентой.

Таким образом, для целей количественной оценки продолжительности жизненного цикла ИС необходимо иметь возможность вычисления параметров уравнения Гомперца - Макегама можно сделать методами нелинейной регрессии. Для вычисления «вручную» и (1991) предлагают нижеследующий алгоритм, дающий вполне удовлетворительную точность. Пусть мы имеем значения чисел доживших «l» для четырех равноотстоящих друг от друга моментов времени: t, t+n, t+2n…

В начале вычисляют вспомогательные величины:

y1 = ln[ l(t)/l(t+n)]; y2 = ln[l(t+n)/(l(t+2n)];

y3 = ln[l(t+2n)/(l(t+3n)]; z = y1+y3-2y2;

w= (y3-y2)/(y2-y1).

Тогда параметры формулы Гомперца-Мекема могут быть найдены из следующих соотношений:
A = (y1 y3 – y22)/(z n),

Ro = [(y2 – y1)2 ln(w)]/[z n (w-1) w (t/n)],

a = ln(w)/n

Tжц=6,8 лет.

Таким образом, наиболее развитой моделью жизненного цикла, реализуемой при втором подходе является модель Гомперца-Макегама (6). Достоинством приведенной модели является ее гибкость, поскольку она имеет в отличие от немодифицированного экспоненциального распределения большее число подгоночных параметров и функций. Однако следует заметить, что ретроспективная информация о продолжительности жизненных циклов сложных технических и информационных систем представляет собой короткий динамический ряд (случайную конечную выборку малого объема), что не позволяет в полной мере использовать классические методы математической статистики для повышения эффективности (в статистическом смысле) оценок параметров рассмотренных моделей.

Кроме того, на продолжительность жизненного цикла сложной информационной системы оказывают влияние большое количество случайных факторов, последовательность и продолжительность проводимых с ней мероприятий (испытаний, доработок, модернизаций, апгрейтов и т. п.).

В соответствии со стандартом ISО 2382/14-78 под производительностью ИС понимают «часть времени эксплуатации, которая фактически используется тем или иным пользователем».

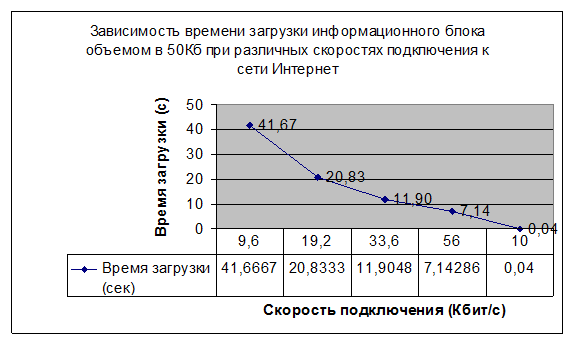
Рис. 5.4 Зависимость времени загрузки.

Из графика видно, при такой величине смыслового информационного блока данных учитываются все перечисленные выше условия.

Допустимый разброс значений смысловых информационных блоков (дисперсия) может составлять до 50 Кб. Максимальный передаваемых данных составит около 100 Кб.

В этом случае требования ко времени загрузки данных все еще выполняются при среднем значении скорости подключения к сети Интернет, что позволяет рассматривать такой вариант в качестве граничного.

5.5. Расчет энтропии системы.

Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:

Энтропия Н(Х) обладает рядом свойств, оправдывающих ее выбор в качестве характеристики степени неопределенности. Во-первых, она обращается в нуль, когда одно из состояний системы достоверно, а другие — невозможны. Во-вторых, при заданном числе состояний она обращается в максимум, когда эти состояния равновероятны, а при увеличении числа состояний — увеличивается. Наконец, и это самое главное, она обладает свойством аддитивности, т. е. когда несколько независимых систем объединяются в одну, их энтропии складываются.

В проекте рассматриваются 4 состояния системы:

·  Запуск системы 1 × 10-2.

·  Ожидание 40 ×10-2 (программа не выполняется, идет ожидание запросов).

·  Работа с запросами 58,9 ×10-2.

·  Ошибка 10-2 (критическая остановка системы).

Максимальная энтропия системы равна:

Hmax(X)=log n=log 4=0,6020

т. е. максимальное значение энтропии системы с конечным числом состояний равно логарифму числа состояний и достигается, когда все состояния равновероятны.

5.6.Расчет энтальпии системы.

Энтальпия - количественная характеристика, показывает нагруженность.

I или i – энтальпия.

, где

- свободное место (пространство) в байтах, отведенное под систему с наполнением.

- место, отведенное под систему, программы, среду разработки.

k – число контейнеров.

j – число модулей в конкретном контейнере.

- среднее значение модулей по одному контейнеру.

- среднее число контейнеров.

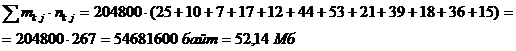
Энтальпия служебной информации по отношению к энтальпии информационного блока несравнимо мала, следовательно, ее во внимание не принимается.

Коэффициент использования системы меньше единицы, значит, это позволит уменьшить нагруженность системы и повысить ее надежность

5.7. Производительность системы.

Коэффициент программной избыточности: КИЗБ=0.04 – часть вычислительной мощности системы расходуемой на проверку входных данных для защиты от непредумышленных, случайных искажений вычислительного процесса, программ и данных – система оперативной защиты(данные берутся из книги Н. Олифера и В. Олифера «Компьютерные сети. Принципы, технологии, протоколы. Второе издание»). Системы оперативной защиты предназначены для выявления и блокирования распространения негативных последствий проявления дефектов и уменьшения их влияния на надежность функционирования ПС до устранения их первичных источников.

Вероятность некритического сбоя системы: КСБ=0.005

Время восстановления после сбоя: ТСБ=2-4 с – время на перезагрузку интерфейса системы.

Вероятность отказа системы: КОТК=0.001

Время восстановления после отказа: ТОТК= от 20-30с до 180с – время перезапуска сервера баз данных (20-30с.) или полная перезагрузка всей машины (до 180с.)

Коэффициент надежности линии связи: КЛС=0,8 – вероятность отката, зависания, искажения информации из-за шумов на линии, ведущее к повторной передаче данных.

Таким образом, общее среднее время задержки передачи данных составляет:

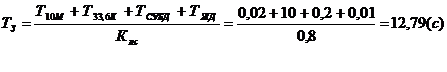
Эффективное число одновременно обслуживаемых запросов при 40% загрузке канала:

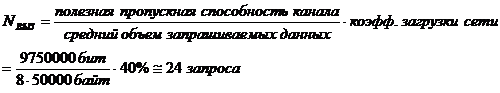
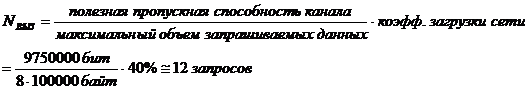
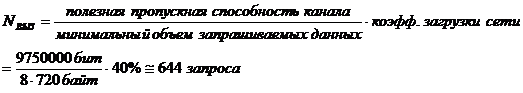
При значении коэффициента загрузки канала свыше 50% резко падает его пропускная способность, поэтому рассматривается граничный вариант. Расчет производился для пакетов данных объемом в VД=50Кб, соответствующих математическому ожиданию системы.

Среднее число запросов в час:

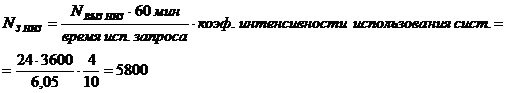
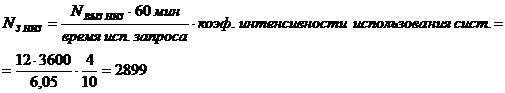
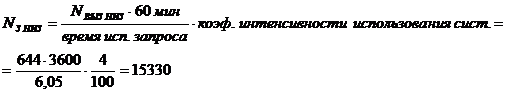
Коэффициент готовности системы:

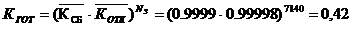
Итоговая производительность системы при данных условиях:

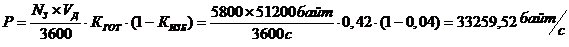
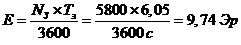
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9