Виртуальные лабораторные работы по физике (стр. 4 )

Контрольные вопросы

1.  Запишите закон поглощения γ-квантов.

2.  Назовите процессы, за счет которых происходит поглощение γ-квантов?

3.  Запишите выражение, которое устанавливает связь между линейным коэффициентом поглощения и массовым.

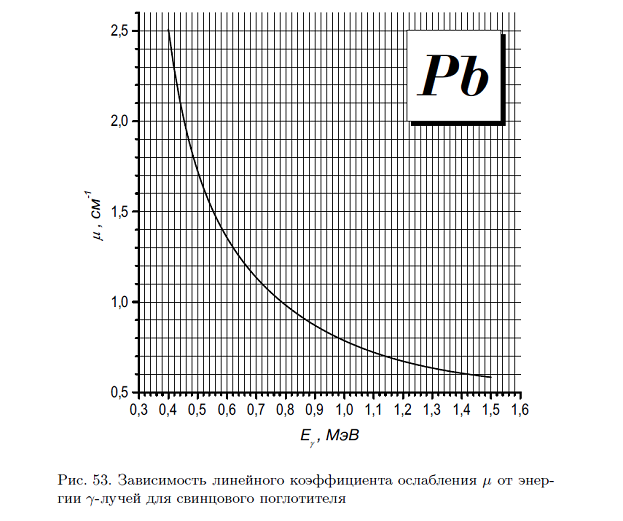
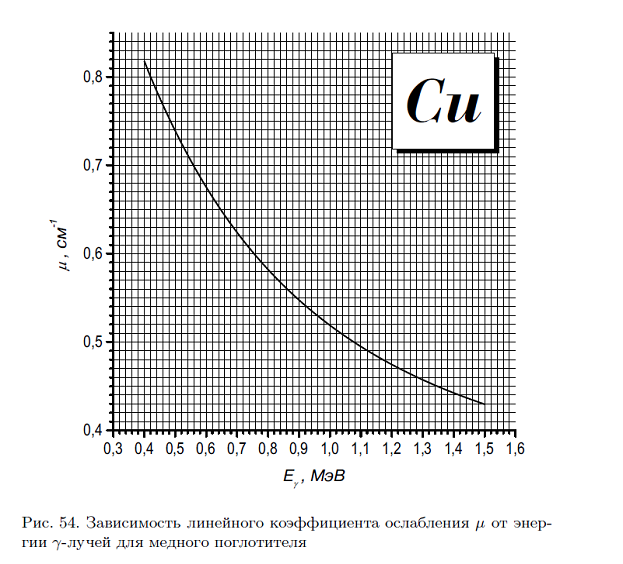
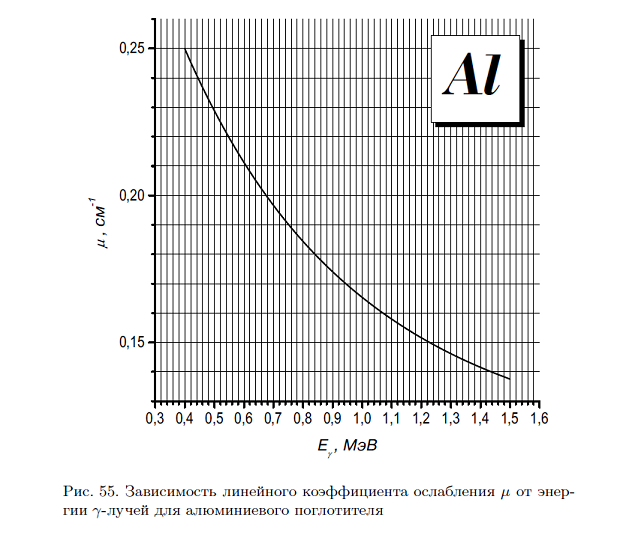
4.  Объясните наличие минимума на графике зависимости коэффициента ослабления от энергии

5.  Почему при нахождении энергии γ-лучей измеряют поглощение не в одном веществе, а в 2–3 веществах?

6. Может ли происходить фотоэффект на свободных электронах?

7. Объясните механизм образования γ–кванта?

8. Чему равен полный коэффициент поглощения?

Литература

1.  . Введение в ядерную физику. М. Энергоатомиздат,1993

Лабораторная работа № 5

Исследование жёсткой компоненты космического излучения

Цель работы: изучить угловое распределение жесткой компоненты космических лучей, определить время жизни покоящегося мюона.

Введение

Космические лучи—это поток частиц, приходящих на Землю из межзвездного пространства. Первичные космические лучи состоят главным образом из протонов (∼90%), α-частиц и более тяжелых ядер. Основная доля первичных космических лучей имеет энергию10 9 – 1010 эВ, но встречаются также частицы со значительно большей энергией (до 1019 эВ). Частицы с энергиями менее 109 эВ отклоняются магнитным полем Земли и не попадают на нее. Поток протонной компоненты с энергией выше 2·109 эВ составляет примерно один протон на 1 см2/с. В результате взаимодействия первичных космических лучей с ядрами атмосферы появляются новые (вторичные) частицы — мюоны различных сортов, распад которых приводит к появлению электронов, позитронов и фотонов большой энергии. Таким образом, вторичные космические лучи, наблюдаемые на высоте до 10 км, совершенно не похожи по своему составу на первичные космические лучи. Космическое излучение, приходящее в нижние слои атмосферы, принято делить на мягкую и жесткую компоненты.

Мягкая компонента состоит из электронов, позитронов и γ-квантов, которые сильно поглощаются в веществе. Поглощение частиц мягкой компоненты существенным образом зависит от порядкового номера Z вещества поглотителя. Частицы мягкой компоненты почти целиком поглощаются десятисантиметровым слоем свинца.

Жесткая компонента состоит из мюонов, которые слабо поглощаются веществом, притом приблизительно одинаково веществами с разными Z.

Столь большое различие проникающей способности частиц обеих компонент связано с тем, что электроны и позитроны мягкой компоненты при взаимодействии с веществом тратят большую часть своей энергии на излучение, а потери мюонов на излучение сравнительно малы. Это объясняется тем, что количество излученной энергии пропорционально квадрату заряда и обратно пропорционально квадрату массы частицы, а мю-мюон примерно в 207 раз тяжелее электрона.

Потери энергии на ионизацию и возбуждение атомов вещества для электронов и мюонов космических лучей на уровне моря примерно одинаковы и сравнительно малы. Особенностью мюонов является их распад на электроны, нейтрино и антинейтрино:

В плотной среде поглощение мюонов обусловлено потерей энергии на ионизацию атомов среды. В газообразной среде пробег мюонов велик и нужно учитывать их выбывание из потока космических лучей за счет спонтанного распада.

§ 1. Угловое распределение жесткой компоненты космических лучей на уровне моря

Можно считать, что основная часть мюонов рождается в верхних слоях атмосферы и имеет энергию 1 —10 ГэВ. Мюоны, входящие в состав жесткой компоненты, возникают в результате распада пионов — продуктов ядерного взаимодействия первичных космических лучей с ядрами атмосферы:

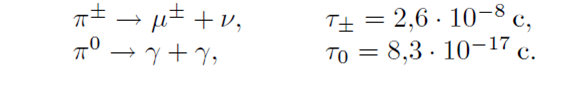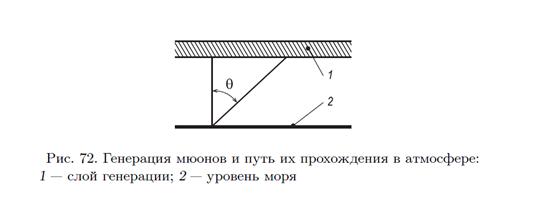
Следовательно, мюоны проходят почти весь слой атмосферы (∼900 г/см2). При этом они частично поглощаются, частично распадаются. Мюоны, идущие под углом θ к вертикали (рис. 72) и попадающие на уровень моря, проходят в атмосфере путь в l/cos θ раз больший, чем мюоны, идущие по вертикали. Поэтому вероятность распада для мюонов, идущих под углом θ, больше. При увеличении угла θ будет увеличиваться также слой воздуха, который должны пройти мюоны. Это приводит к увеличению поглощения за счет ионизационных потерь. Таким образом, оба фактора должны привести к уменьшению интенсивности мюонов с увеличением зенитного угла θ.

Можно, однако, выделить которые поглотились за счет увеличения количества вещества. Измерения интенсивности вертикального потока мюонов, выполненные на разных глубинах под землей, показали, что число мюонов N(x) уменьшается как функция количества пройденного плотного вещества x (г/см2) по следующему закону:

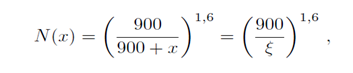
где ξ=900+x— полное количество вещества, пройденного мюоном от места генерации до места поглощения (масса вертикального столба воздуха принята равной 900 г/см2). Из рис. 72 видно, что ξ=900/cos θ. Таким образом, число мюонов, дошедших до счетчика на уровне моря, уменьшается за счет поглощения в веществе по закону

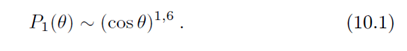
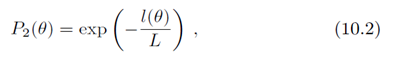С увеличением длины пути, пройденного мюоном, увеличивается вероятность распада мюона. Вероятность прохождения мюоном пути l без распада равна

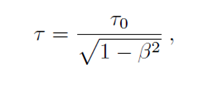где L = vτ — длина распадного пробега; v = βc — скорость мюона; τ — время жизни движущегося мюона. Из релятивистской механики известно, что

где τ0 — время жизни покоящегося мюона. Тогда

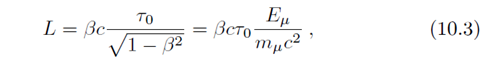
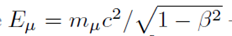
где — полная энергия мюона, Eμ можно принять равной 4·109 эВ; mμ — масса покоящегося мюона, которая в энергетических единицах составляет 105,8 МэВ/c2.

Отношение числа мюонов, идущих под зенитным углом θ, к числу вертикально падающих мюонов можно записать в виде

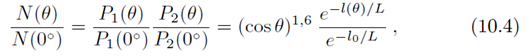
где P1(θ) и P2(θ) определены формулами (10.1) и (10.2). Из полученной формулы можно выразить L

(*)

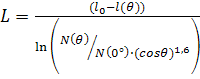Можно считать, что по вертикали мюоны проходят путь l0=15 км. Путь мюонов под углом θ равен

Воспользовавшись формулами (10.3) и (10.5), а также экспериментально определенным отношением N(θ)/N(0◦), с помощью формулы (10.4) можно получить значение τ0:

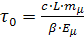(10.6)

Нужно помнить, что проведенные расчеты дают значение τ0 только по порядку величины, поскольку они не учитывают, как меняется вероятность распада мюонов из-за уменьшения их энергии вследствие ионизационного торможения.

§ 2. Указания по выполнению работы

В настоящей работе изучается угловое распределение жесткой компоненты вторичных космических лучей. Работа выполняется с помощью «телескопа», состоящего из двух детекторов, включенных на совпадения (см. блок-схему на рис. 73).

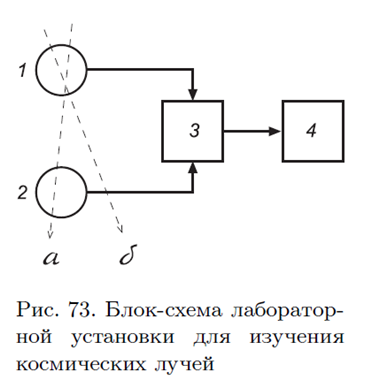Космические частицы регистрируются детекторами 1 и 2. Если частица пройдет через оба детектора (частица а), то схема совпадений 3 вырабатывает импульс. Если частица проходит через один из детекторов и не попадает в другой детектор (частица б), тогда схема совпадений импульс не вырабатывает. Таким образом, число импульсов, сосчитанных пересчетным прибором 4, будет равно числу частиц, прошедших через оба детектора и зарегистрированных ими.

Инструкция по работе с виртуальной установкой

27. 

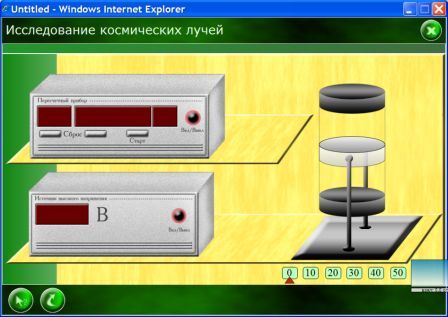
В режиме «Ознакомления» (первая кнопка внизу слева) изучите названия приборов. На пересчётном приборе выясните какой дисплей будет показывать время (время измеряется в секундах), а какой число накапливаемых импульсов при распаде ядер.

28.  Для проведения измерений выйдите из режима «Ознакомления». Щелчком мыши включить высоковольтный источник напряжения и пересчетный прибор (0 на рис.)

29.  Нажмите старт для проведения эксперимента. После снятия показаний нажмите сброс. На дисплее 1 высвечивается степень множителя, например, цифра 8 означает, что число импульсов на дисплее 2 надо умножить на 108.

30.  Чтобы повернуть «телескоп» на , 30, 40 или 50) щёлкните по соответствующему указателю.

Задание. Изучение углового распределения жесткой компоненты космических лучей и определение времени жизни мюона.

При помощи установки найти угловую зависимость интенсивности жесткой компоненты космических лучей, т. е. зависимость счета совпадений N от зенитного угла θ (в том числе для θ=0◦).

Измерения счета совпадений надо производить с как можно большей статистической точностью. Длину распадного пробега и время жизни мюона определить одним из способов, указанных в §3.

Измерения и вычисления занести в таблицу:

Времени жизни мюона можно найти из формулы (10.6).

Контрольные вопросы

1. Состав и энергия первичных космических лучей.

2. Мягкая и жесткая компоненты космических лучей.

3. Механизм образования мезонов в космических лучах. Характеристики распада π- и μ-мезонов.

4. Почему электроны и позитроны космических лучей относятся к «мягкой» компоненте и поглощаются целиком приблизительно в 10 см свинца, а μ-мезоны той же энергии относятся к «жесткой» компоненте и свободно проходят через этот слой?

5. Время жизни μ-мезонов, учет эффекта, следующего из специальной теории относительности.

6. Зависимость вероятности поглощения и распада от расстояния, пройденного μ-мезонами в атмосфере.

Литература

1. H. Л.Григоров, , . Космические лучи. М., Физматгиз, 1962.

2. . Мю-мезон. М., АН СССР. 1963.

3. . Космические лучи. М., Гостехиздат, 1954.

4. , . Происхождение космических лучей. Изд. АН СССР. М., 1963.

5. , . Космические лучи и их взаимодействие. М., Атомиздат, 1968.

6. . Введение в физику космических лучей. Изд. МГУ, 1988.

Лабораторная работа №6

Определение заряда электрона методом Милликена

Цель работы: Определение элеменарного заряда (заряда электрона)

методом Милликена.

Приборы и оборудование: виртуальная модель современной

установки Милликена, секундомер.

Определение элементарного заряда может быть выполнено при помощи ряда методов:

1. Измерением заряда сосчитанных непосредственно частиц;

2. Статистической обработкой результатов наблюдений шротт-эффекта (дробовый шум в электронных лампах);

3. Из равенства N=F, где F - число Фарадея (определяется непосредственно), а N - число Авагадро (может быть очень точно определено, например, из наблюдений дифракции на кристалле рентгеновских лучей известной дины волны);

4. Из измерения скорости перемещения заряженных микроскопических

частиц в однородном электрическом поле.

В данной работе используется последний метод, так как он является

одновременно наиболее прямым и убедительным доказательством того, что

электрические заряды дискретны.

[Дискретность электрического заряда:

Любой электрический заряд (Q) тела равен целому кратному заряда электрона (e=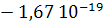Кл ):

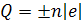, где n=1, 2, 3… ]

В основу метода положено изучение движения заряженных капелек жидкости (масла) в однородном электрическом поле. Измеряя скорости капелек, падающих в поле силы тяжести (при отсутствии электрического поля), и скорости капелек, поднимающихся в поле сил тяжести (при наличие электрического поля), можно вычислить действующую на капельку силу электрического поля. Зная величину напряжённости электрического поля, можно определить заряд капельки.

Измерение элементарного заряда по этому способу и доказательство дискретности электрического заряда были проведены в классических опытах Р. Милликена в гг.

На движущую заряженную каплю масла, помещённую в однородное электрическое поле, действуют следующие силы:

1)Сила трения со стороны воздуха; по закону Стокса она равна:

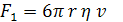(1)

где радиус частицы, вязкость воздуха ( =1,82 · 10-5 кг/м·с),

скорость капли;

2)Сила тяжести:

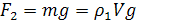(2)

где масса капли, ускорение свободного падения (=9,8 м/),

объём капли (V=), плотность масла (=1,03·кг/);

4)Выталкивающая сила (сила Архимеда) со стороны воздуха:

(3)

где плотность воздуха (=1,293 кг/);

5)Сила со стороны электрического поля (поле заряженного конденсатора):

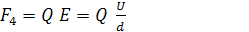(4)

где Q - заряд капли, Е - напряжённость электрического поля, U - напряжение на пластинах конденсатора, d - расстояние между пластинами.

При установившемся движении капли вниз со скоростью :

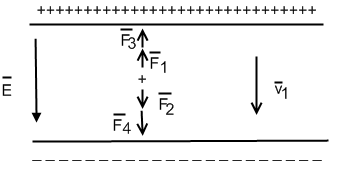
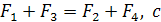ледовательно:

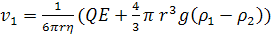(5)

При установившемся движении капли вверх со скоростью :

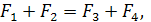
следовательно:

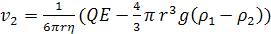(6)

Из формул (5) и (6) можно получить формулы для определения заряда и радиуса капель через скорости движения капли вверх и вниз:

;

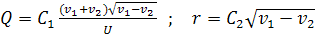где ,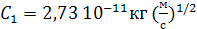

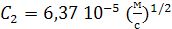
Указания по выполнению работы

Блок схема экспериментальной установки:

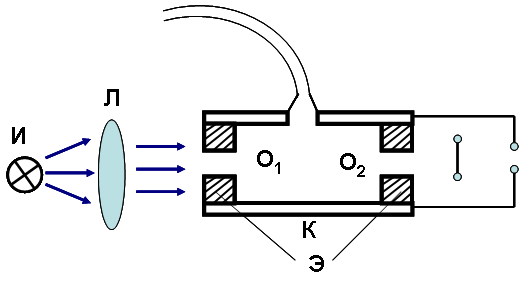
В пространство между пластинами конденсатора через отверстие в верхней пластине вводятся капли масла. За их движением наблюдают в оптическую трубу. Частицы освещаются пучком света от источника и видны в затемненном поле как светящиеся точки. Для уменьшения движения воздуха внутри конденсатора, пространство между пластинами ограничено с боков эбонитовым кольцом (Э), имеющим три окошка (два служат для прохождения светового пучка (О1 и О2), а третье, перпендикулярное к первым двум, используется для наблюдения движения капель).

Порядок выполнения работы

1. Установите на компьютер "виртуальную модель современной установки Милликена".

2. Установите на блоке питания напряжение 150 В (нажмите кнопку "150").

3. Подайте положительный потенциал на верхнюю пластину конденсатора в установке Милликена (нажмите "Черную кнопку" переключателя направления электрического поля). При этом включится подсветка поля микроскопа.

4. Нажмите на грушу, впрыснув масло в пространство наблюдения. Из видимых капель выделите ту, которая будет двигаться вертикально.

5. С помощью секундомера определите время движения t1 выбранной капли вниз при прохождении определённого расстояния S1. А также время движения t2 этой же капли вверх при прохождении определённого расстояния S2. Пройденное каплей расстояние определяется как произведение цены деления (0,029 мм) микрометра на число пройденных делений шкалы. Занесите данные в таблицу 1. Повторите опыт с тремя каплями.

6. Повторите эксперимент для нескольких (трех) капель при напряжении 300 В. Данные занесите в таблицу 1. Используя данные таблицы 1, сделайте расчёт скоростей капель v1 и v2 , радиусов (r) и зарядов (Q) капель по формулам, приведённым в описании работы. Так как заряд капли есть целое число n элементарного заряда e (заряда электрона): Q=ne, то можно определить заряд электрона. Заполните таблицу 2.

7. Рассчитайте погрешности полученных результатов.

Таблица 1

U, B	Номер капли
150
-150
300
-300

Таблица 2

Номер капли

Контрольные вопросы

1.  Почему при движении капельки масла в поле конденсатора её скорость

устанавливается постоянной?

2.  Для чего в опытах Милликена используется плоский конденсатор?

Как рассчитать электрическую силу, действующую на капельку?

3.  При каких условиях заряженная капля движется вверх?

4.  Как движется в электрическом поле свободный электрон без начальной скорости?

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4