Моделирование

процессов и систем

Методические указания и перечень тем курсовых работ
для студентов заочной формы обучения
специальности 080– «Прикладная информатика»
(в менеджменте)

направления 230– «Прикладная информатика»
(в менеджменте)

заочная форма обучения

Выполнение курсовой работы является одной из важнейших форм организации самостоятельной работы студентов. Курсовая работа предназначена для закрепления знаний, полученных при изучении курса «Моделирование экономических процессов и систем». В процессе подготовки курсовой работы студенты более глубоко знакомятся с важнейшими и наиболее сложными проблемами. Курсовая работа призвана способствовать развитию системного мышления, логичного и четкого изложения своих мыслей при исследовании теоретических вопросов, умению применять различные методы в анализе социально – экономических явлений.

При написании работы могут быть использованы различные монографии и статьи, которые посвящены вопросам методологии и практики проведения исследований в области моделирования экономических процессов и систем.

ВЫБОР ТЕМЫ РАБОТЫ

Студенты выполняют курсовую работу под руководством преподавателя. Тематика курсовых работ утверждена кафедрой (Приложение А). Каждый студент в соответствии со своими наклонностями и индивидуальными способностями может выбрать любую заинтересовавшую его тему из предлагаемого перечня курсовых работ. Не исключается возможность выполнения курсовой работы по теме, предложенной студентом.

В процессе выполнения курсовой работы студенты обязаны согласовать с руководителем объект и предмет исследования, план по каждой части работы, основные положения по проблеме и используемые литературные источники.

Каждая тема имеет свои особенности, определяемые объектом исследования, наличием и полнотой источников информации, требованиями руководителя. Вместе с тем каждая работа должна быть построена по единой для всех тем структуре и содержать введение, основную часть, заключение и список использованных источников.

СТРУКТУРА И СОДЕРЖАНИЕ КУРСОВОЙ РАБОТЫ

Независимо от темы курсовые работы должны включать следующие разделы:

ВВЕДЕНИЕ, которое должно содержать обоснование актуальности проблемы исследования; цель курсовой работы; формулировку предмета исследования и обоснование объекта исследования; перечень задач, решаемых в работе для достижения поставленной цели; а также теоретическую, методологическую и информационную базы исследования.

В ОСНОВНОЙ ЧАСТИ курсовой работы необходимо раскрыть выбранную тему, осветив только те вопросы, которые непосредственно относятся к исследуемой проблеме.

В курсовых работах, посвященных применению методов анализа динамики и прогнозирования в исследовании экономических, социальных процессов, не следует давать общую характеристику всех статистических методов прогноза, писать о роли прогностической методологии вообще. Необходимо раскрыть только те методы прогнозирования, которые могут быть применены, исходя из цели и задач исследования, характера имеющейся информации. Особое внимание следует уделить особенностям применения этих методов при анализе конкретных явлений и процессов с учетом их специфики и предпосылок применения конкретных методов прогнозирования.

Если выбранная тема курсовой работы предполагает рассмотрение целой группы методов анализа и прогнозирования, то изложение должно вестись с точки зрения описания особенностей применения для изучения конкретного объекта. При раскрытии данного вида следует не только перечислять методы, используемые для изучения сложных объектов и явлений, но и провести их сравнительный анализ, показать преимущества и недостатки применения каждого их них при решении конкретных прикладных задач.

В курсовой работе могут быть использованы различные методы исследования в зависимости от выбранного объекта и исходной информационной базы, но основой является обоснование целесообразности применения этих методов.

В конце каждого параграфа курсовой работы необходимо сделать краткие выводы.

В курсовой работе, посященной имитационному моделирования систем массового обслуживания должны присутствовать разделы:

-  логико-математического описание и его теоретического обоснование,

-  выбор средств реализации (программной среды),

-  анализ работы модели.

В ЗАКЛЮЧЕНИИ формулируются общие выводы по работе, дается оценка полученных результатов, исходя из целей и задач курсовой работы, а также возможные пути дальнейшего исследования.

Если при проведении исследования у студента возникают какие-либо затруднения, ему следует обратиться за помощью к преподавателю кафедры – руководителю курсовой работы.

Завершает курсовую работу библиографический список, включающий в себя не менее 8 источников.

Громоздкие статистические данные, расчеты и методики прогнозных значений, суть которых излагается в основной части курсовой работы целесообразно выносить в «Приложения».

ОФОРМЛЕНИЕ КУРСОВОЙ РАБОТЫ

Объем курсовой работы не должен превышать 25 страниц формата А4.

Курсовая работа начинается с титульного листа (Приложение Б). Содержание работы помещается на следующей странице.

Прямые цитаты, приводимые из научной литературы дословно, должны быть заключены в кавычки и иметь ссылку на источник информации. Сноска может быть также дана непосредственно в тексте работы. В этом случае в квадратных скобках необходимо сделать следующую запись: [5, с.50]. Первая цифра означает номер источника в приводимом в конце работы списке литературы, а вторая - номер страницы.

Следует помнить, что необходимо избегать большого количества цитат.

Если студент излагает информацию первоисточника своими словами, то ссылка на источник также нужна. Авторский текст следует излагать кратко, сжато, своими словами. Следует помнить, что дословный пересказ содержания первоисточников и тем более переписка отдельных отрывков или разделов из них не допускается.

Ссылка на первоисточник обязательна и для всех статистических данных, используемых в исследовании.

Для представления данных целесообразно использовать таблицы, которые должны иметь:

а) номер таблицы – для удобства ссылки на нее в тексте работы;

б) название таблицы, которое должно содержать указание территории и времени, к которым относятся данные;

в) четкие измерения для каждого показателя.

Для представления данных можно использовать и графический способ. В названии графика, диаграммы необходимо обязательно указать место и время, к которым относится информация.

При построении графиков должен быть соблюден масштаб. Для каждой масштабной шкалы необходимо указать единицы измерения показателей. У пограничных отметок масштабных шкал проставляются цифровые значения каждого параметра.

Если в курсовой работе автор приводит несколько графиков или диаграмм, то целесообразно присвоить им номера.

В тексте курсовой работы автор приводит результаты расчетов, дает их подробный анализ и интерпретацию. Все вычисления приводятся в приложениях к курсовой работе. Если в работе проведено несколько однотипных расчетов, то методика их реализации в тексте приводится только один раз.

Все формулы записываются отдельными строками и должны иметь номер, который указывается справа от нее в круглых скобках.

Например:

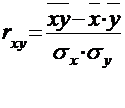
, (1.1)

Число в скобках – это порядковый номер параграфа и формулы.

Список использованной литературы должен включать как цитируемые источники, так и все монографии, учебные пособия, статистические сборники и т. д., которые были использованы при написании курсовой работы. Список литературы составляется в алфавитном порядке.

ПРИЛОЖЕНИЕ А

Темы курсовых работ

Раздел 1.

1.  Статистическое моделирование и прогнозирование как метод научного познания.

2.  Статистическое прогнозирование и планирование экономического и социального развития.

3.  Этапы развития методологии прогнозирования.

4.  Вероятностный характер статистических моделей.

5.  Точность статистического прогнозирования.

6.  Методологические особенности краткосрочного прогнозирования.

7.  Методологические особенности долгосрочного прогнозирования.

8.  Комплексное прогнозирование социально – экономических явлений и процессов.

9.  Статистические методы прогнозирования в отраслях экономики (на примере одной из отраслей).

10. Прогнозирование спроса в розничной торговле.

11. Прогнозирование в социологии.

12. Статистическое прогнозирование в экологии.

13. Особенности статистического прогнозирования в социологии (социологическое, социальное прогнозирование).

14. Моделирование и прогнозирование спроса населения.

15. Экономико-математические методы в маркетинге.

16. Модели прогноза эффективности рекламы в системе маркетинговых коммуникаций.

17. Сравнительный анализ моделей рекламной компании.

18. Моделирование и прогнозирование спроса, предложения и цены.

19. Паутинообразная математическая модель ценообразования по Вальрасу на рынке совершенной конкуренции.

20. Модели динамического анализа финансово-хозяйственной деятельности предприятий.

21. Методы прогнозирования возможного банкротства предприятия.

22. Моделирование и прогнозирование деловой активности биржевых структур.

23. Статистический анализ и прогнозирование смертности населения в России (регионе, районе, городе) (на примере...).

24. Статистический анализ и прогнозирование численности населения в России (регионе, районе, городе) (на примере...).

25. Статистический анализ тенденций рождаемости и ее прогнозирование (на примере РФ, региона, района, города).

26. Статистический анализ и прогнозирование брачности и разводимости (на примере РФ или региона).

27. Прогнозирование уровня заболеваемости детей и подростков наркоманией.

28. Прогнозирование уровня заболеваемости населения города (района, региона, РФ).

29. Прогнозирование младенческой смертности.

30. Прогнозирование развития товарного рынка

Раздел 2. Моделирование систем массового обслуживания

Вариант 1

На фабрике в кладовой работает один кладовщик. Он выдает запасные части механикам, обслуживающим станки и устанавливающим эти части на испорченных станках (запасные части слишком дороги и, кроме того, их ассортимент слишком велик для того, чтобы каждый механик мог иметь запасную часть каждого вида в своем ящике). Время, необходимое для удовлетворения запроса, зависит от типа запасной части. Запросы бывают двух категорий. Соответствующие данные представлены в таб.1.
 

Кладовщик обслуживает механиков по принципу "первым пришел - первым обслужен" независимо от категории запроса. Так как сломанный станок ничего не производит, то простой механика в очереди оценивается в 5 руб.. в секунду. Эта стоимость не зависит от того, за какой запасной частью ушел механик. Руководитель считает, что среднее число простаивающих механиков можно уменьшить, если запросы категории 2 в кладовой будут удовлетворяться быстрее запросов категории 1. Необходимо создать модель работы кладовой для обеих дисциплин обслуживания очереди и выполнить моделирование для каждой из них в течение восьмичасового рабочего дня. Уменьшится ли число ожидающих механиков в очереди? Сколько денег ежедневно будет сэкономлено при использовании приоритетного обслуживания?
 

Вариант 2

В авторемонтной мастерской стоит одна полировочная машина для полирования некоторой детали мотора машины. Для этого надо выполнить следующие этапы:

1.  вынуть деталь (12+3 мин.);

2.  установить ее в полировочной машине (10 + 4 мин.);

3.  фаза 1 полирования (80 + 20 мин.);

4.  поворот детали для продолжения полирования (15 + 7 мин.);

5.  фаза 2 полирования (110 + 30 мин.);

6.  достать отполированную деталь из машины (10 + 4 мин.);

7.  установить деталь в прежнее место (12 + 3 мин.) .

Деталь слишком тяжела для того, чтобы ее мог поднять один оператор полировочной машины. Требуется подъемный кран, помогающий ему в работе. В частности подъемный кран нужно использовать  на этапах 1, 2, 4, 6 и 7. Имеется только один подъемный кран. Краном пользуется не только  оператор полировочной машины, его используют и на других работах в мастерской. Для других видов работ может потребоваться кран через каждые 39 + 10 мин. Время, на которое забирают кран, равно 25 + 10 мин.
Постройте модель такой системы. Обеспечьте сбор данных о времени ожидания оператора полировочной машины освобождения крана. Разделите сбор данных об ожидании на этапе 4 и этапе 6. (Предполагается, что если на этапе 6 кран получен, то оператор его уже не отпускает до завершения этапа 2. Соберите также данные об ожидании крана другими видами работ.) Моделирование проведите для 400 ч модельного времени. Сравните значения трех указанных видов данных по каждой из следующих дисциплин обслуживания:

1.   первым пришел - первым обслужен;

2.   оператор полировочной машины имеет наивысший приоритет при использовании крана.

Вариант 3

Корабли двух типов прибывают в порт, где происходит их разгрузка. В порту имеются два буксира, обеспечивающих ввод и вывод кораблей из порта. Первый тип кораблей включает корабли малой тоннажности и требует при входе и выходе одного буксира. Второй тип кораблей имеет больший размер, и для их ввода и вывода из порта требуются два буксира. Из-за различия размеров кораблей необходимы причалы различного размера, кроме того корабли имеют разное время погрузки - разгрузки. Данные приведены в таблице 2.
 

Постройте модель системы, в которой можно оценить время ожидания кораблями каждого типа входа в порт. Среднее время ожидания включает время ожидания освобождения причалов и/или буксира. Корабль, ожидающий освобождения причала, не обслуживается буксиром до тех пор, пока не будет предоставлен нужный причал. Более того, корабли второго типа не будут занимать буксир до тех пор, пока не будут доступны оба буксира. Если ожидание кораблями типов 1 и 2 стоит 7000 руб. и 10000 руб. в час соответственно, а стоимость эксплуатации буксира равна 5000 руб. в день, следует ли воспользоваться третьим добавочным буксиром в порту?

Вариант 4

Необходимо решить, какое число мест на стоянке следует отвести для автомобилей, ожидающих мойки. Поток автомобилей является пуассоновским со значением среднего интервала, равным 5 мин. Время мойки автомобиля распределено экспоненциально со значением среднего, равным 4 мин. Если клиенты подъезжают и не застают свободного места для ожидания, они уезжают и моют автомобиль в другом месте. Необходимо написать модель такой системы и использовать ее для исследования системы при использовании одного, двух и трех мест на стоянке. В каждом из этих случаев надо моделировать работу в течение восьмичасового рабочего дня и оценить долю клиентов, оставшихся без обслуживания. Определить, сколько мест должно быть на стоянке, если в мастерской установлено три мойки автомобилей. Какова при этом будет загрузка каждой мойки.
 

Вариант 5

Небольшой продовольственный магазин состоит из трех прилавков и одной кассы на выходе из магазина. Покупатели входят в магазин, входной поток имеет пуассоновский характер, причем среднее значение интервала составляет 75 с. Войдя в магазин, каждый покупатель берет корзинку и может обойти один или несколько прилавков, отбирая продукты. Вероятность обхода конкретного прилавка показана в таб. 3. Время, требуемое для обхода прилавка, и число покупок, выбранных у прилавка, распределены равномерно (см. табл. 3).
 

После того, как товар отобран, покупатель становится в конец очереди к кассе.. Время обслуживания покупателя в кассе пропорционально числу сделанных покупок, на одну покупку уходит 3 с проверки. После оплаты продуктов покупатель оставляет корзинку и уходит.
Постройте модель, описывающую процесс покупок в продовольственном магазине. Проведите моделирование восьмичасового рабочего дня и определите нагрузку кассира и максимальную длину очереди перед кассой. Считая, что число корзинок неограничено, определите максимальное число корзинок, находящихся у покупателей одновременно.

Вариант 6

На фабрике имеются две кладовые, в каждой из которых работает один кладовщик. Один кладовщик обслуживает механиков, работающих на больших станках, а другой всех прочих механиков. Входящий в каждую кладовую поток является пуассоновским со значением интенсивности, равным 20 механикам в час. Время обслуживания механиков распределено по экспоненциальному закону со значением среднего, равным 2 мин.
Ввиду того, что механики очень долго ждут обслуживания, было сделано предложение объединить две кладовые так, чтобы любой кладовщик мог обслуживать любой запрос механика. Предполагается, что интенсивность прихода в такую сдвоенную кладовую также удвоится и будет составлять в среднем 40 механиков в час, а среднее время обслуживания останется по-прежнему равным 2 мин.
Оцените оба варианта (существующий и предлагаемый) с точки зрения общего числа механиков, находящихся в кладовой, и ожидаемого среднего времени простоя каждого из них (т. е. включая среднее время их обслуживания).

Вариант 7

На сборочный участок цеха поступают партии, каждая из которых состоит из 3 деталей. Интервалы времени поступления партий распределены экспоненциально со средним значением 15 мин. Половина всех поступающих деталей перед сборкой должна пройти предварительную обработку в течении 10 мин. На сборку подаются обработанная и необработанная детали. Процесс сборки занимает 8 мин.
Смоделировать работу участка в течение 24 часов. Определить возможные места появление очередей, выявить причины их возникновения, предложить меры по их устранению и смоделировать скорректированную систему.

Вариант 8

На обрабатывающий участок цеха поступают детали в среднем через 35 мин. Обработка деталей производится на одном из двух станков. Первый станок обрабатывает деталь в среднем 30 мин и имеет 4% брака, второй соответственно 50 мин и 8% брака. Все бракованные детали возвращаются на повторную обработку на второй станок. Детали, попавшие дважды в разряд бракованных, считаются отходами. Все интервалы времени распределены по экспоненциальному закону.
Смоделировать обработку на участке 500 деталей. Определить загрузку станков, вероятность появления отходов. Предложить меры по рациональному использованию оборудования.

Вариант 9

На вычислительном центре в обработку принимаются три класса заданий А, В и С. Исходя из наличия оперативной памяти ЭВМ задания классов А и В могут решаться одновременно, а задания класса С монополизируют ЭВМ. Задания класса А поступают через 20 + 5 мин, класса В - через 20 + 10 мин, класса С - через 28 + 5 мин и требуют для выполнения: класс А - 20 + 5 мин, класс В - 21 + 3 мин, класс С -
28 + 5 мин. Задачи класса С загружаются в ЭВМ, если она полностью свободна. Задачи классов А и В могут дозагружаться к решающей задаче.
Смоделировать работу ЭВМ за 80 ч. Определить ее загрузку.

Вариант 10

В парикмахерскую с 3 креслами могут приходить клиенты двух типов. Клиенты первого типа желают только стричься, распределение интервалов их прихода  35 + 10 мин. Клиенты второго типа желают стричься и бриться, распределение интервалов их прихода  60 + 20 мин. Очередь для всех клиентов общая к первому освободившемуся парикмахеру. На стрижку уходит в среднем 30 мин, а на бритье - 12 мин ( время распределено по экспоненциальному закону). Парикмахерская открывается в 8 ч 30 мин, а закрывается в 17 ч 00 мин. Парикмахеры обедают по очереди соответственно в 12 ч 00 мин, в 12 ч 30 мин и в13 ч 00 мин. Время перерыва на обед 30 мин.  Если к началу обеда парикмахер был занят, то перед тем, как устроить перерыв, он заканчивает обслуживание клиента. Клиенты, которые приходят в парикмахерскую в течение перерыва, ждут его окончания. Выполнить моделирование парикмахерской в течение рабочего дня. Определить загрузку парикмахеров, среднее время, необходимое клиенту на обслуживание. Определить оптимальные параметры потоков клиентов для данной парикмахерской.

Вариант 11

На фабрике в кладовой работает один кладовщик. Он выдает запасные части механикам, обслуживающим станки и устанавливающим эти части на испорченных станках (запасные части слишком дороги и, кроме того, их ассортимент слишком велик для того, чтобы каждый механик мог иметь запасную часть каждого вида в своем ящике). Время, необходимое для удовлетворения запроса, зависит от типа запасной части. Запросы бывают трех категорий. Соответствующие данные представлены в таб. 5.
 

Кладовщик обслуживает механиков по принципу "ближайшая операция - кратчайшая" . Так как сломанный станок ничего не производит, то простой механика в очереди оценивается в 5 коп. в секунду. Эта стоимость не зависит от того, за какой запасной частью ушел механик. . Необходимо создать модель работы кладовой для заданной дисциплине обслуживания очереди и выполнить моделирование в течение восьмичасового рабочего дня. Повторить моделирование для дисциплины обслуживания "ближайшая операция - наидлиннейшая". Уменьшится ли число ожидающих механиков в очереди? Какая из дисциплин является более экономичной?

Вариант 12

В парикмахерской, в которой принята система предварительной записи, работают три мастера. У каждого мастера есть свои клиенты, интенсивности прихода которых распределены по экспоненциальному закону и равны в среднем соответственно 45 мин, 55 мин, 60 мин. Квалификация мастеров примерно одинаковая, поэтому время обработки одного клиента в среднем для всех равно 60 + 30 мин (распределение времени равномерное). Иногда в парикмахерскую заходят клиенты, не записавшиеся заранее. Их интенсивность прихода  - 2 человека в час. Таких клиентов обслуживает свободный мастер. Парикмахерская открывается в 8 ч 30 мин, а закрывается в 17 ч 00 мин. Парикмахеры обедают по очереди соответственно в 12 ч 00 мин, в 12 ч 30 мин и в13 ч 00 мин. Время перерыва на обед 30 мин.  Если к началу обеда парикмахер был занят, то перед тем, как устроить перерыв, он заканчивает обслуживание клиента. Клиенты, которые приходят в парикмахерскую в течение перерыва, ждут его окончания. Выполнить моделирование парикмахерской в течение рабочего дня. Определить загрузку парикмахеров, среднее время, необходимое клиенту на обслуживание. Определить оптимальные параметры потоков клиентов для данной парикмахерской.

ПРИЛОЖЕНИЕ Б

Образец титульного листа

Государственное бюджетное образовательное учреждение высшего профессионального образования московской области
«Международный университет природы, общества и человека «Дубна»

Институт системного анализа и управления

Кафедра системного анализа и управления

Курсовая работа

по моделированию процессов и систем

на тему:

«Статистический анализ и прогнозирование рождаемости в России »

Выполнила: студентка группы 3071

Иванова Ксения

Руководитель: доцент

Дубна, 2011

12.   Математико-статистические методы в социально-экономических исследованиях - М.: Финансы и статистика: ИНФРА-М, 20с.

13.  Егоров национальной экономики. – М.: ИНФРА –М, 2001.

14.  , , . Математические методы в экономике. – М.: «Дело и Сервис», 2001. – 368 с.

15.  Канторович по курсу «Анализ временных рядов» Экономический журнал ВШЭ, 2002.

16.  . Основы имитационного моделирования сложных экономических систем. – М.: Дело, 2003. – 336 с.

17.  , Сениченков систем. − СП.: Дело, 2006.

18.  . Экономико-математическое моделирование. – М.:ЮНИТИ-ДАНА. 2005. – 295 с.

19.  , Трофимец в Excel: Учебное пособие. - М.: Финансы и статистика, 20с

20.  Парсаданов и планирование социально – экономической системы страны. – М., 2001.

21.  , , . Имитационное моделирование: учеб. пособие. – М.: Издательский центр «Академия». 2006. – 236 с.

22.  , . Моделирование систем. – М.: Высш. шк.. 2007. –343 с.

23.  Ханк – прогнозирование – М.: Изд. дом «Вильямс», 20с.

КРАТКИЙ (!) пример выполнения курсовой работы

по моделированию экономических процессов и систем

на тему:

Моделирование работы ЭВМ

Оглавление

Введение.. 18

Постановка задачи.. 19

Теоретическая часть. 20

Логико-математическое описание модели.. 21

Выбор средств моделирования.. 22

Анализ работы модели.. 23

Заключение.. 25

Список литературы... Ошибка! Закладка не определена.

Введение

Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропор­тах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и обо­рудования, на складах снабженческо-сбытовых организаций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Изучением таких ситуаций занимается теория массового обслуживания.

Имитационное моделирование является одним из мощнейших методов анализа экономических систем. В общем случае, под имитацией понимают процесс проведения на ЭВМ экспериментов с математическими моделями сложных систем реального мира. Цели проведения подобных экспериментов могут быть самыми различными – от выявления свойств и закономерностей исследуемой системы, до решения конкретных практических задач. С развитием средств вычислительной техники и программного обеспечения, спектр применения имитации в сфере экономики существенно расширился. В настоящее время ее используют как для решения задач внутрифирменного управления, так и для моделирования управления на макроэкономическом уровне. Как следует из определения, имитация – это компьютерный эксперимент. Единственное отличие подобного эксперимента от реального состоит в том, что он проводится с моделью системы, а не с самой системой. В данной курсовой работе будет построена модель работы ЭВМ.

Постановка задачи

На вычислительном центре в обработку принимаются три класса заданий А, В и С. Исходя из наличия оперативной памяти ЭВМ задания классов А и В могут решаться одновременно, а задания класса С монополизируют ЭВМ.

Задачи класса С загружаются в ЭВМ, если она полностью свободна. Задачи классов А и В могут дозагружаться к решающей задаче.
Смоделировать работу ЭВМ за 80 ч. Определить ее загрузку.

Теоретическая часть

Каждая система массового обслуживания состоит из какого-то числа обслуживающих единиц, которые называются каналами обслуживания. В качестве каналов могут фигурировать: линии связи, различные приборы, лица, выполняющие те или иные операции.

Всякая СМО предназначена для обслуживания какого-то потока заявок, поступающих в какие-то случайные моменты времени. Обслуживание заявок продолжается случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени обслуживания приводит к тому, что в какие-то периоды времени на входе СМО скапливается излишне большое число заявок (они либо становятся в очередь, либо покидают СМО не обслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать.

Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем.

Имитационное моделирование — это метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику. Имитационное моделирование — это метод исследования, основанный на том, что изучаемая система заменяется имитатором и с ним проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с имитатором называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте).

Имитационное моделирование — это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае математическая модель заменяется имитатором или имитационной моделью.

Имитационная модель — логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.

Логико-математическое описание модели

Входной поток заявок формируется следующим образом: задачи для выполнения приходят через случайные промежутки времени, не зависящие друг от друга (см. Постановка задачи). Если процессор свободен, то первая пришедшая задача идет на выполнение. Время обработки для каждой задачи задается случайно и также не зависит от каких-либо параметров (см. Постановка задачи). Задачи А и В могут выполнятся одновременно, а задача С монополизирует систему. Если процессор занят и задача не может поступить на обработку, то она становится в очередь. Работа ЭВМ моделируется заданное в программе время, по истечении которого считается количество обработанных и поступивших задач, загрузку системы и очередь в каждый момент времени. Для анализа необходимости модернизирования системы в модель включена возможность работы двух процессоров для обработки поступающих задач. Для наглядности на графиках представляется время поступления каждой задачи, загрузка системы и накопление очереди.

Выбор средств моделирования

Для описания работы ЭВМ использовалась имитационная схема системы массового обслуживания. Для реализации данной курсовой работы была выбрана среда разработки Delphi, так как она позволяет с легкостью оперировать большими массивами данных, получаемых при моделировании работы ЭВМ за большой промежуток времени. Также данная среда была выбрана из-за возможности простого изменения модели системы, в том числе внедрения второго процессора, обрабатывающего задачи, стоящие в очереди, что позволяет проанализировать преимущества второго канала обработки заявок.

Анализ работы модели

Имеется одноканальная система массового обслуживания. Заявки трех типов поступают для обработки через случайные промежутки времени. При заданных временных интервалах к концу моделирования в системе всегда присутствует очередь, что означает полную загрузку системы и невозможность справиться с таким потоком заявок.

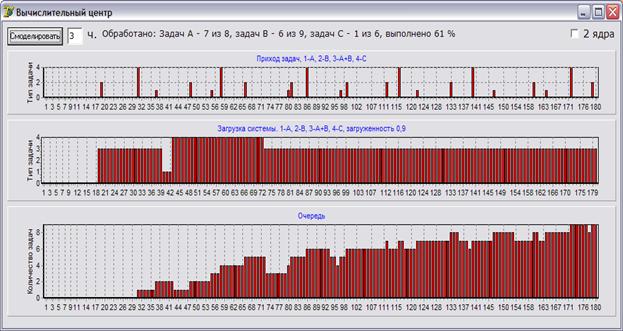Рис. 1.

При включении второго процессора пик очереди не всегда приходится на конец моделирования, а следовательно система может справляться с таким потоком.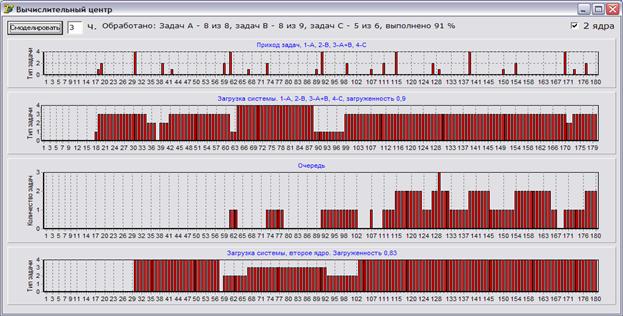

Рис. 2.

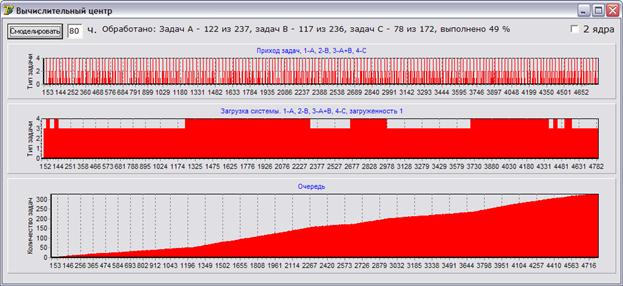
Аналогичная ситуация наблюдается и при моделировании полных 80 часов работы ЭВМ.

Одноканальная система способна обработать только половину всех пришедших требований.

Рис. 3.

При включении в систему второго канала обслуживания система справляется почти полностью с входящим потоком заявок.

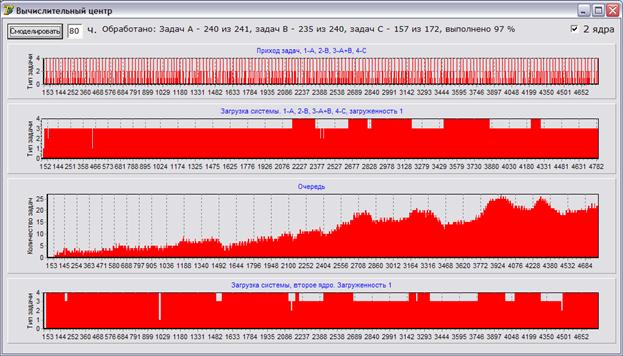
Рис. 4.

Заключение

В данной курсовой работе была построена модель работы ЭВМ. В среде Delphi разработано приложение, позволяющее проанализировать загрузку системы, возникающую очередь, влияние подключения второго процессора. Для наглядности построены графики времени прихода задач, загрузки системы, распределения очереди во времени. Время моделирования регулируется от 1 до 80 часов.