Банк выдал предприятию кредит в сумме 200 тыс. руб., сроком на 1 год, под процентную ставку 19% годовых. Проценты за пользование кредитом начисляются ежемесячно. Найти сумму, которую клиент должен гасить ежемесячно при которой к окончанию срока, кредит будет погашен полностью.
Дано:
Сумма кредита (Sотыс. руб.;
процентная ставка (t% годовых;
срок кредита (Тмесяцев;
период начисления процентов за пользование кредитом (N) - 1 раз в месяц.
Рассчитать сумму ежемесячного платежа (П)- ?
Решение:
Выведем формулу для нахождения суммы ежемесячного платежа.
Сумма вклада с процентами в конце первого периода начисления будет равна
S1=So+So· a = Sо (1+ a)
После начисления процентов полученная сумма уменьшается на величину платежа (П),
сумма оставшаяся после платежа за первый месяц составит
S1=Sо (1+a)-П,
где a - процентная ставка в долях за период начисления
Сумма вклада с процентами в конце второго периода начисления составит
S2=[ Sо ( 1+a)-П ] (1+a),
сумма оставшаяся после платежа за второй месяц составит
S2=[ Sо ( 1+a)-П ] (1+a)-П
Сумма вклада с процентами в конце третьего периода начисления составит:
S3={ [Sо (1+a) - П] (1+a) - П }(1+a).
Сумма, оставшаяся после платежа за третий месяц составит:
S3={ [ Sо (1+a) - П] (1+a) - П}(1+a) - П
и т. д.
Раскроем скобки:
S1=Sо (1+a) - П
S2=Sо (1+a)(1+a) - П(1+a) - П
S3=Sо (1+a)(1+a)(1+a)-П(1+a)(1+a)-П(1+a)-П
и т. д.
Вынесем П за скобки, вместо получившейся единицы подставим выражение ( 1+a)![]() , т. к ( 1+a)
, т. к ( 1+a)![]() =1:
=1:
S1=Sо (1+a) - П
S2=Sо (1+a)![]() -П[ (1+a)
-П[ (1+a)![]() + (1+a)
+ (1+a)![]() ]
]
S3= Sо (1+a)![]() -П[(1+a)
-П[(1+a)![]() + (1+a)
+ (1+a)![]() +( 1+a)
+( 1+a)![]() ]
]
.![]() .
.
Sn= Sо (1+a)![]() -П[ (1+a)
-П[ (1+a)![]() +(1+a)
+(1+a)![]() + ... + (1+a)
+ ... + (1+a)![]() +(1+a)
+(1+a)![]() ] ,
] ,
из этого выражения выделим П:
П = 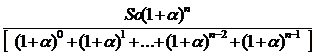
Знаменатель получившегося выражения является числовым рядом, образованным из членов геометрической прогрессии. Применим к нему формулу для суммы членов геометрической прогрессии.
Формула геометрической прогрессии:
 Sn =
Sn =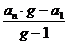
где:
![]() =
=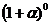 =1 - 1-ый член геометрической прогрессии
=1 - 1-ый член геометрической прогрессии
![]() - n-ый член геометрической прогрессии
- n-ый член геометрической прогрессии
g = 1+a - одно и то же постоянное число
Подставив значения ![]() ,
, ![]() , g в знаменатель, получим
, g в знаменатель, получим ![]()
![]() =
=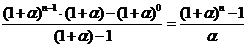
Таким образом, знаменатель вышеуказанного выражения можно представить в следующем виде ![]()
Подставим получившийся знаменатель в вышеуказанное выражение :
П =![]() =
= 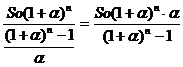
Итак, формула для нахождения суммы ежемесячного платежа (П) имеет вид
 П=
П=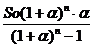
где a - процентная ставка в долях за период начисления
n - количество периодов начисления
Приступим непосредственно к решению задачи
1.Найдем месячную процентную ставку:
a в месяц = 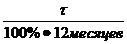
a мес. = 19%годовых / 100% . 12 месяцев = 0,016
2.Найдем количество периодов начисления процентов:
n = T/N
n=12 / 1= 12
Найдем сумму ежемесячного платежа:
П=![]()
П = [200 000 * (1+0,016)12*0,016] / [(1+0,016)12 – 1]=руб.
Ответ: сумма ежемесячного платежа равнаруб.
Итак, для того чтобы полностью погасить кредит к окончанию срока необходимо ежемесячно платить банкурублей.
Проверочная таблица к примеру 2 ( в руб.)
№ периода | Сумма на начало периода (So) | Начисленный процент (a) | Накопленная сумма (ст.2+ст.3) | Сумма платежа (П) | Остаток суммы (ст. 4 - ст.5) |
1 | 200000 | 3200 | 203200 | 18450 | 184750 |
2 | 184750 | 2956 | 187706 | 18450 | 169256 |
3 | 169256 | 2708 | 171964 | 18450 | 153514 |
4 | 153514 | 2456 | 155970 | 18450 | 137520 |
5 | 137520 | 2200 | 139721 | 18450 | 121271 |
6 | 121271 | 1940 | 123211 | 18450 | 104761 |
7 | 104761 | 1676 | 106437 | 18450 | 87987 |
8 | 87987 | 1408 | 89395 | 18450 | 70945 |
9 | 70945 | 1135 | 72080 | 18450 | 53630 |
10 | 53630 | 858 | 54488 | 18450 | 36038 |
11 | 36038 | 577 | 36615 | 18450 | 18165 |
12 | 18165 | 291 | 18455 | 18450 | 5, т. е. 0 |
(Погрешность из-за округления.)
Условиями договора о вкладе может быть предусмотрено, что на сумму вклада можно делать взносы. В приведенной задаче рассматриваются взносы которые вносятся регулярно одинаковыми суммами через одинаковые периоды. Последовательность денежных поступлений, осуществляемых равными суммами через равные периоды времени, называют постоянной финансовой рентой, а сумму всех таких поступлений - наращенной величиной финансовой ренты.
Пример 3
На вклад в конце каждого месяца вносится сумма 10 тыс. руб. Банк ежемесячно начисляет проценты по ставке 7 % годовых. Срок вклада 1 год. Найти накопленную сумму вклада.
Дано:
Сумма ежемесячного взноса (Птыс. руб.;
период начисления процентов на вклад (N)- 1 месяц;
срок вклада (Тмесяцев;
процентная ставка (t% годовых.
Найти накопленную сумму вклада (S нак.) - ?
Решение:
1.Найдем месячную процентную ставку:
a в месяц = 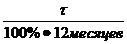
a мес. =7%годовых / 100% . 12 месяцев = 0,006
2.Найдем количество периодов начисления процентов:
n = T/N
n=12 / 1= 12
3. Найдем накопленную сумму вклада.
Суммы вклада с процентами при последовательных взносах будет равна:
за первый месяц:
S1= По
за второй месяц :
S2 = Пo + Пo × a= Пo(1+ a)![]()
за третий месяц :
S3= П1+ П1 a = Пo+ Пo × a+(Пo+ Пo × a) a=Пo(1+ a)![]()
за четвертый месяц:
S4= П2+ П2 a= Пo+ Пo × a+(Пo+ Пo × a) a+[ Пo+ Пo × a+(Пo+ Пo × a) a]a= =Пo(1+ a)![]()
....Sn= Пo(1+ a)![]()
Накопленная сумма вклада (S нак.) равна сумме всех значений S
Суммируем все значения S
S нак. = По +Пo(1+ a)![]() + Пo(1+ a)
+ Пo(1+ a)![]() + Пo(1+ a)
+ Пo(1+ a)![]() + ... + Пo(1+ a)
+ ... + Пo(1+ a)![]()
Вынесем П за скобки, единицу заменим выражением (1+ a)![]() , т. к. (1+ a)
, т. к. (1+ a)![]() =1
=1
S нак. = По ((1+ a)![]() +(1+ a)
+(1+ a)![]() +(1+ a)
+(1+ a)![]() +(1+ a)
+(1+ a)![]() + ... + (1+ a)
+ ... + (1+ a)![]() ),данное выражение является числовым рядом образованным из членов геометрической прогрессии.
),данное выражение является числовым рядом образованным из членов геометрической прогрессии.
Применим к сумме всех значений П формулу для суммы членов геометрической прогрессии
формула геометрической прогрессии-
 Sn =
Sn =![]()
где, ![]() =
=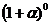 =1 - 1-ый член геометрической прогрессии
=1 - 1-ый член геометрической прогрессии
![]() - n-ый член геометрической прогрессии
- n-ый член геометрической прогрессии
g = 1+a - одно и то же постоянное число (знаменатель геометрической прогрессии)
Подставим значения ![]() ,
, ![]() , g в выражение:
, g в выражение:
S нак.= По ((1+ a)![]() +(1+ a)
+(1+ a)![]() +(1+ a)
+(1+ a)![]() +(1+ a)
+(1+ a)![]() + ... + (1+ a)
+ ... + (1+ a)![]() )=
)=
= По![]()
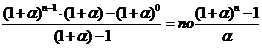
Таким образом формула для нахождения накопленной суммы вклада при поступлении последовательных взносов на вклад через равные периоды времени в конце периода начисления следующая
 S нак. =
S нак. =![]()
S нак. = 10 000*[(1+0,006)12 – 1]/0,006=
Ответ: Накопленная сумма вклада составит рублей.
Проверочная таблица к примеру 3
№ периода | Сумма на начало периода (So) | Начисленный процент (a) | Накопленная сумма (ст.2+ст.3) | Сумма взноса (П) | Накопленная сумма ( S нак.) ( ст.4+ ст.5) |
1 | 10000 | 10000 | |||
2 | 10000 | 60 | 10060 | 10000 | 20060 |
3 | 20060 | 120,4 | 20180 | 10000 | 30180 |
4 | 30180 | 181 | 30361 | 10000 | 40361 |
5 | 40361 | 242 | 40604 | 10000 | 50604 |
6 | 50604 | 304 | 50907 | 10000 | 60907 |
7 | 60907 | 365 | 61273 | 10000 | 71273 |
8 | 71273 | 428 | 71700 | 10000 | 81700 |
9 | 81700 | 490 | 82191 | 10000 | 92191 |
10 | 92191 | 553 | 92744 | 10000 | 102744 |
11 | 102744 | 616 | 103360 | 10000 | 113360 |
12 | 113360 | 680 | 114040 | 10000 | 124040 |
Каждая из вышеприведенных задач имеет задачу обратную. Рассмотрим их.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 |




