Методическая разработка по дисциплине «Управление портфелем недвижимости» (стр. 3 )

2.  В процессе рассмотрения возможности инвестиций в объект недвижимости инвестор оценил вероятностное распределение его доходности (таблица 5). Исходя из этих оценок вычислить ожидаемую доходность объекта недвижимости и его дисперсию.

Методические рекомендации к задаче 2.

Дисперсия доходности любого актива (var) может быть определена по одной из двух следующих формул:

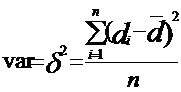, (1)

где: - доходность актива в i –том периоде наблюдений;

- средняя доходность актива, определяется как средняя арифметическая доходность актива за периоды наблюдений;

n – количество наблюдений (при большом числе наблюдений в знаменателе формулы дисперсии применяется (n-1);

- стандартное (среднее квадратическое) отклонение доходности актива.

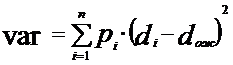, (2)

где: pi - вероятность получения доходности актива по i –тому варианту развития событий;

di - доходность актива по i –тому варианту развития событий;

dож - ожидаемое значение доходности актива, определяется как средне-взвешенная величина с учетом вероятностей получения доходностей.

Таблица 5

Доходность и вероятность ее получения по объекту недвижимости

(в о. е.)

3.  Портфель составлен из трех объектов недвижимости А, В и С. Портфельный вес объекта А 50%; объекта В 30%; объекта С 20%. Динамика доходностей объектов представлена в таблице 6. Рассчитать, как изменятся риск и доходность портфеля при замене объекта А на объект D при сохранении портфельного веса объекта D на уровне портфельного веса А.

Таблица 6

Динамика доходностей по объектам недвижимости

(в процентах)

4.  Вычислить стандартное отклонение портфеля из трех активов по заданной ковариационной матрице (таблица 7). Портфельный вес актива А 50%, В 30%, С 20%.

Таблица 7

Ковариационная матрица доходностей активов

5.  Исходя из имеющейся информации, представленной в таблице 8, определить ожидаемую доходность каждого актива и портфеля в целом.

Таблица 8

Величины стоимости активов

(в млн. руб.)

6.  Строится портфель из активов А и В с ожидаемыми доходностями 0,12 и 0,18 и стандартными отклонениями 0,25 и 0,4 соответственно. Коэффициент корреляции доходностей активов 0,8. Оценить ожидаемую доходность и стандартное отклонение для портфеля с равными долями инвестиций в активы А и В.

7.  Произведена следующая оценка совместного вероятностного распределения доходностей от инвестиций в активы А и В (таблица 9). Оцените ковариацию и коэффициент корреляции доходности данных активов.

Методические рекомендации к задаче 7.

Для расчета ковариации доходности активов А и В может быть использована одна из двух следующих формул:

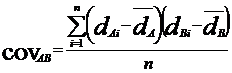, (3)

где: - доходность актива А в i –том периоде наблюдений;

рынок недвижимости.

Практические задания

1.  Покажите на графике зависимость между риском и доходностью с помощью линии рынка капитала.

2.  Дайте сравнительную характеристику ситуаций в точках касания эффективного множества портфелей и кривой безразличия; кривой безразличия и линии рынка капитала; эффективного множества портфелей и линии рынка капитала.

3.  Представьте вывод формулы доходности эффективного портфеля (модель САРМ). Поясните модель САРМ на графике с помощью линии рынка актива. Какие риски учитывает: а) линия рынка каптала; б) линия рынка актива?

4.  Коэффициент корреляции доходности актива А и актива В равен 0,80; стандартное отклонение актива А 0,39; актива В 0,25. Рассчитайте ковариацию доходности актива А и актива В.

5.  Портфель составлен из двух активов А и В; стандартное отклонение актива А составляет 0,39; его портфельный вес 0,25. Ковариация доходности активов А и В 0,07; стандартное отклонение актива В 0,25. Рассчитайте коэффициент корреляции доходности актива А и актива В.

6.  Портфель составлен из безрискового актива и рискового актива, доля которого в составе портфеля равна 0,3; доходность составляет 0,2; а его стандартное отклонение 0,4. Рассчитайте риск портфеля.

7.  Стандартное отклонение портфеля, составленного из безрискового актива и рискового актива, составляет 90% величины стандартного отклонения среднерыночного портфеля. Безрисковая ставка дохода составляет 0,06; ожидаемая доходность рыночного портфеля 0,16. Рассчитайте ожидаемую доходность портфеля.

8.  Стандартное отклонение портфеля, составленного из безрискового актива и рискового актива, 0,40; стандартное отклонение среднерыночного портфеля 0,44. Безрисковая ставка дохода 0,06; ожидаемая рыночная премия за риск 0,10. Рассчитайте ожидаемую доходность портфеля.

9.  Рассматриваются два актива А и В с ожидаемыми доходностями 15% и 20% и стандартными отклонениями 30% и 40% соответственно. Вычислить стандартное отклонение портфеля, состоящего из двух активов, взятых в одинаковой пропорции, если корреляция между ними составляет 0,75.

10.  Рассчитать стандартное отклонение и ожидаемую доходность портфеля, составленного из рыночного портфеля и безрискового актива, ожидаемые ставки доходности которых составляют 0,17 и 0,09 соответственно. Стандартное отклонение рыночного портфеля 0,25; портфельный вес безрискового актива составляет 30%.

Контрольные вопросы

1.  Дайте определение агрегированного портфеля.

2.  Что характеризует точка касания кривой безразличия с линией рынка капитала? Поясните на графике.

3.  Что характеризует точка пересечения линии рынка капитала с осью ожидаемой доходности? Поясните на графике.

4.  Представьте графически и охарактеризуйте механизм формирования оптимального портфеля, составленного из рисковых активов: а) для инвестора с никой степенью избегания риска; б) с высокой степенью избегания риска.

5.  Что понимается под хорошо диверсифицированным рыночным портфелем?

6.  Как определяется величина стандартного отклонения портфеля, составленного из рисковых активов?

7.  Как рассчитывается доходность портфеля недвижимости?

Тесты

1.  Комбинации риска и доходности, которые существуют на рынке для широко диверсифицированных портфелей, характеризует:

1)  эффективное множество портфелей

2)  достижимое множество портфелей

3)  кривая безразличия

4)  линия рынка капитала

5)  линия рынка актива

2.  Точка касания линии рынка капитала с линией эффективного множества портфелей характеризует:

1)  вложение инвестиций только в безрисковые активы

2)  оптимальный портфель, составленный из рисковых активов

3)  оптимальный портфель, составленный из безрисковых и рисковых активов

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9