Эконометрика и экономико-математические методы и модели (стр. 1 )

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«ВИТЕБСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»

ЭКОНОМЕТРИКА

И

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ

Методические указания и контрольные задания для студентов

экономических специальностей заочной формы обучения

Витебск

2012

УДК 658.012

Эконометрика и экономико-математические методы и модели: методические указания и контрольные задания для студентов экономических специальностей заочной формы обучения.

Витебск: Министерство образования Республики Беларусь, УО «ВГТУ», 2012.

Составители: асс. ,

асс.

Методические указания составлены в соответствии с типовой программой курса «Эконометрика и экономико-математические методы и модели». Данные указания содержат задания по выполнению контрольной работы студентами экономических специальностей заочной формы обучения. Подробно рассмотрены типовые примеры по каждому заданию. Приводится необходимый теоретический материал.

Могут быть использованы всеми категориями студентов, магистрантов, аспирантов, преподавателей и сотрудников.

Одобрено кафедрой информатики УО «ВГТУ» 2 сентября 2011 г., протокол

Рецензент: к. т.н., доцент

Редактор: к. т.н., доцент

Рекомендовано к опубликованию редакционно-издательским советом

Ответственный за выпуск:

Учреждение образования «Витебский государственный технологический университет»

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

По курсу «Эконометрика и экономико-математические методы и модели» предусмотрено выполнение контрольной работы. Целью контрольной работы является освоение студентами правил экономико-математического моделирования хозяйственных и экономических задач, связанных с планированием и управлением производства, решения этих задач математическими методами.

В связи с отсутствием стабильных учебников и учебных пособий по данному курсу задачи контрольной работы снабжены методическими указаниями по их решению. Кроме того, приведены типовые примеры решения этих задач.

Для определения номера варианта необходимо разделить число, состоящее из двух последних цифр вашего шифра, на 20. Номер варианта совпадает с остатком, полученным от деления. В случае отсутствия остатка номер варианта будет 0.

Контрольная работа должна включать следующие обязательные структурные части:

·  титульный лист;

·  содержание (созданное с использованием стилевого форматирования);

·  основную часть (каждое задание должно начинаться с указания номера варианта и располагаться с новой страницы);

·  список использованных источников, приложение.

Контрольная работа включает три задания:

Задание 1. Сетевые модели. Сетевое планирование и управление.

Задание 2. Эконометрические модели. Корреляционно-регрессионный анализ.

Задание 3. Оптимизационные модели. Линейное программирование.

На титульном листе контрольной работы указываются название кафедры (кафедра информатики), наименование дисциплины («Эконометрика и экономико-математические методы и модели»), название факультета, номер курса, шифр группы, номер зачетной книжки, фамилия (если фамилия была изменена, то обязательно необходимо указать старую фамилию), имя, отчество (см. приложение 1).

1 СЕТЕВЫЕ МОДЕЛИ.

СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ

1.1 Назначение и область применения

Сетевое планирование – это комплекс графических и расчетных методов организационных мероприятий, обеспечивающих моделирование, анализ и динамическую перестройку плана выполнения сложных проектов и разработок, например, таких как:

ü  строительство и реконструкция каких-либо объектов;

ü  выполнение научно-исследовательских и конструкторских работ;

ü  подготовка производства к выпуску продукции;

ü  перевооружение армии.

Характерной особенностью таких проектов является то, что они состоят из ряда отдельных, элементарных работ. Они обуславливают друг друга так, что выполнение некоторых работ не может быть начато раньше, чем будут завершены некоторые другие.

1.2 Сетевая модель и ее основные элементы

Основными понятиями сетевых моделей являются следующие: события, работы и пути. Построение сетевой модели (структурное планирование) начинается с разбиения проекта на четко определенные работы, для которых определяется продолжительность.

Работа – это некоторый процесс, приводящий к достижению определенного результата, требующий затрат каких-либо ресурсов и имеющий протяженность во времени. Работа в сетевом графике изображается стрелкой.

По своей физической природе работы можно рассматривать как:

Ø  действие – это процесс, требующий затрат времени и ресурсов (заливка фундамента бетоном, составление заявки на материалы, изучение конъюнктуры рынка);

Ø  процесс (старение отливок, выдерживание вина, травление плат);

Ø  ожидание – это процесс, который требует только затрат времени и не нуждается в использовании ресурсов (ожидание поставки комплектующих, пролеживание детали в очереди к станку).

По количеству затрачиваемого времени работа может быть:

v  действительной, т. е. требующей затрат времени;

v  фиктивной, т. е. формально не требующей затрат времени и представляющей связь между какими-либо работами (передача измененных чертежей от конструкторов к технологам, сдача отчета о технико-экономических показателях работы цеха вышестоящему подразделению).

Фиктивная работа может реально существовать, например, «передача документов от одного отдела к другому». Если продолжительность такой работы несоизмеримо мала по сравнению с продолжительностью других работ проекта, то формально ее принимают равной 0. Существуют фиктивные работы, которым в реальности не соответствуют никакие действия. Такие фиктивные работы только представляют связь между другими работами сетевой модели. Работы связаны друг с другом таким образом, что выполнение одних работ может быть начато только после завершения некоторых других.

Событие – это момент времени, когда завершаются одни работы и начинаются другие. Событие представляет собой результат проведенных работ и в отличие от работ не имеет протяженности во времени. Например, фундамент залит бетоном, старение отливок завершено, комплектующие поставлены, отчеты сданы и т. д. Событие обозначается кружком. Номер события проставляется внутри кружка. Использование понятия «событие» в качестве важнейшего элемента плана существенно отличает сетевой график от других методов планирования.

Таким образом, начало и окончание любой работы описываются парой событий, которые называются начальным и конечным событиями. Поэтому для идентификации конкретной работы используют код работы (ij), состоящий из номеров начального (i-гo) и конечного (j-гo) событий, например 2-4; 3-8; 9-10 (рис. 1.1).

На этапе структурного планирования взаимосвязь работ и событий изображается с помощью сетевого графика, где работы изображаются стрелками, которые соединяют вершины, изображающие события. Около каждой стрелки ставится среднее время выполнения соответствующей работы. Любое событие может считаться наступившим только тогда, когда закончатся все входящие в него работы. Поэтому работы, выходящие из некоторого события не могут начаться, пока не будут завершены все операции, входящие в это событие (рис. 1.2).

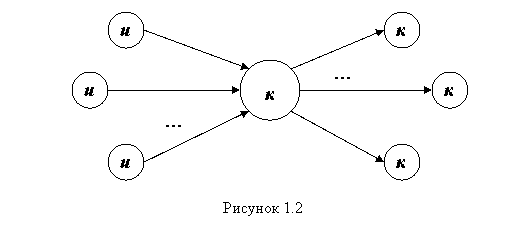
Номер исходного события равен единице. Номера остальных событий соответствуют последней цифре кода предшествующей данному событию работы (или работ).

Событие, не имеющее предшествующих ему событий, т. е. с которого начинается проект, называют исходным событием. Событие, которое не имеет последующих событий и отражает конечную цель проекта, называется завершающим событием. Событие, характеризующее собой факт окончания всех предшествующих работ и начало всех последующих работ, называется промежуточным или просто событием (рис. 1.3).

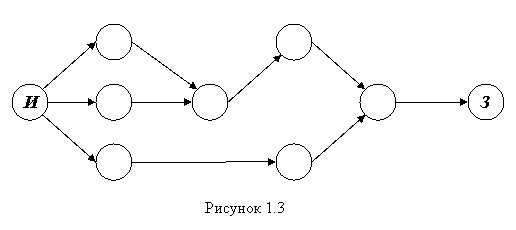
Важное значение для анализа сетевых моделей имеет понятие пути.

Путь – это любая непрерывная последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Путь определяется по направлению стрелок, причем ни один путь не должен дважды проходить через одно и то же событие. Длина пути рассчитывается как сумма продолжительности составляющих его работ. Продолжительность выполнения отдельных работ определяется различными методами: нормативным, методом средних оценок, методом экспертных оценок и др. Трудоемкость выполнения работ проставляется над линией – стрелкой, которая обозначает данную работу.

Различают следующие виды путей:

Ø  Полный путь – это путь от исходного до завершающего события.

Ø  Критический путь – максимальный по продолжительности полный путь.

Ø  Подкритический путь – полный путь, ближайший по длительности к критическому пути.

Работы, лежащие на критическом пути, называют критическими. Каждый путь характеризуется своей продолжительностью (длительностью), которая равна сумме продолжительностей составляющих его работ.

1.3 Правила построения сетевых графиков

При построении сетевого графика необходимо следовать следующим правилам:

ü  длина стрелки не зависит от времени выполнения работы;

ü  стрелка не обязательно должна представлять прямолинейный отрезок;

ü  для действительных работ используются сплошные стрелки, а для фиктивных – пунктирные стрелки;

ü  каждая операция должна быть представлена только одной стрелкой;

ü  не должно быть параллельных работ между одними и теми же событиями, для избежания такой ситуации используют фиктивные работы;

ü  следует избегать пересечения стрелок;

ü  не должно быть стрелок, направленных справа налево;

ü  номер начального события должен быть меньше номера конечного события;

ü  не должно быть висячих событий (т. е. не имеющих предшествующих событий), кроме исходного события;

ü  не должно быть тупиковых событий (т. е. не имеющих последующих событий), кроме завершающего события;

ü  не должно быть циклов (рис. 1.4).

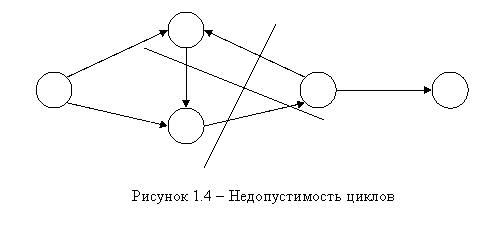
Поскольку работы, входящие в проект, могут быть логически связаны друг с другом, то необходимо всегда перед построением сетевого графика дать ответы на следующие вопросы:

Ø  Какие работы необходимо завершить непосредственно перед началом рассматриваемой работы?

Ø  Какие работы должны непосредственно следовать после завершения данной работы?

Ø  Какие операции могут выполняться одновременно с рассматриваемой работой?

Исходные данные для построения сетевой модели могут задаваться различными способами, например:

ü  описанием предполагаемого проекта. В этом случае необходимо самостоятельно разбить его на отдельные работы и установить их взаимные связи;

ü  списком работ проекта. В этом случае необходимо проанализировать содержание работ и установить существующие между ними связи;

ü  списком работ проекта с указанием их упорядочения. В этом случае необходимо только отобразить работы на сетевом графике.

Построение сетевого графика необходимо начинать с выявления исходных работ модели. Если, согласно условию, некоторая работа может выполняться, не ожидая окончания каких-либо других работ, то такая работа является исходной в сетевой модели, и ее начальным событием является исходное событие. Если исходных работ несколько, то их стрелки выходят все из одного исходного события.

Если, согласно условию, после окончания некоторой работы не должны выполняться никакие другие работы, то такая работа является завершающей работой в сетевой модели, и ее конечным событием является завершающее событие. Если завершающих исходных работ несколько, то их стрелки заходят все в одно завершающее событие.

Если, согласно условию, несколько работ имеют общее начальное и общее конечное события, то они являются параллельными, имеют одинаковый код, что недопустимо. Для устранения параллельности работ вводят дополнительное событие и фиктивную работу (которой в реальности не соответствует никакое действие) таким образом, чтобы конечные события работ различались (рис. 1.5).

1.4 Временные параметры сетевых графиков и методика их

расчета

Применение методов сетевого планирования и управления в конечном счете должно обеспечить получение календарного плана, определяющего сроки начала и окончания каждой операции. Построение сети является лишь первым шагом на пути к достижению этой цели. Вторым шагом является расчет сетевой модели, который выполняют прямо на сетевом графике, пользуясь простыми правилами.

К временным параметрам событий относятся:

Ø  ранний срок наступления события i – ;

Ø  поздний срок наступления события i – ;

Ø  резерв времени наступления события i – .

Ранний срок наступления события – это время, необходимое для выполнения всех работ, предшествующих данному событию i. Оно равно наибольшей из продолжительности путей, предшествующих данному событию.

Поздний срок наступления события – это такое время наступления события i, превышение которого вызовет аналогичную задержку наступления завершающего события сети. Поздний срок наступления любого события i равен разности между продолжительностью критического пути и наибольшей из продолжительностей путей, следующих за событием i.

Резерв времени наступления события – это такой промежуток времени, на который может быть отсрочено наступление этого события без нарушения сроков завершения разработки в целом. Начальные и конечные события критических работ имеют нулевые резервы событий.

Рассчитанные численные значения временных параметров записываются прямо в вершины на сетевом графике следующим образом (рис. 1.6):

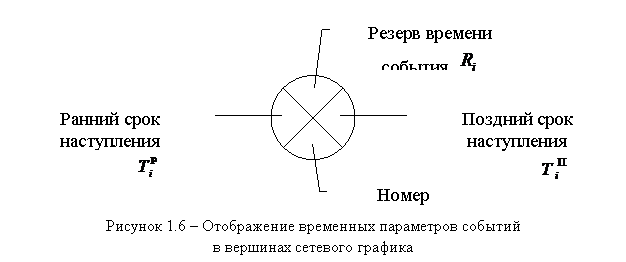
1.5 Методика расчета временных параметров событий

Путем последовательного перехода от исходного события, ранний срок свершения которого равен нулю, к завершающему событию рассчитываются ранние сроки его свершения. Ранний срок наступления события представляет собой минимальный из возможных моментов наступления данного события при заданной продолжительности работ и начальном моменте. Ранний срок наступления j-го события вычисляется по формуле

, (1.1)

где – ранний срок наступления j-го события;

– ранний срок наступления i-го события;

tij – средняя продолжительность работы ij;

k – число работ, непосредственно предшествующих j-му событию (все эти работы на сетевом графике обозначаются стрелками, входящими в кружок, обозначающий j-e событие).

Ранние сроки определяются величиной наиболее длительного отрезка пути от исходного до рассматриваемого события. При определении их около кружков карандашом проставляют длительность всех путей, ведущих от исходного события, и в левый сектор вносят максимальный из путей.

Путем последовательного перехода от завершающего события, поздний срок свершения которого равен величине критического пути, рассчитывают поздний срок его свершения. Этот срок определяется разностью продолжительности критического пути и максимальным из путей, следующим за этим событием

, (1.2)

где – поздний срок наступления i-гo события;

– поздний срок наступления j-гo события;

L – число работ, непосредственно следующих за i-м событием (все эти работы на сетевом графике обозначаются стрелками, выходящими из кружка, обозначающего i-e событие).

При определении поздних сроков свершения события около кружков записывают все возможные значения такой разности и в правый сектор вписывают минимальную величину разности. Поздний срок наступления завершающего события принимается равным раннему сроку наступления этого же события.

Разность между поздним и ранним сроками свершения событий есть резерв времени этого события. Резерв времени i-гo события Ri вычисляется по формуле

. (1.3)

Полный резерв времени работы определяется как разность между поздним сроком свершения события, завершающего работу, и ранним сроком свершения, предшествующего работе события, минус продолжительность самой работы

. (1.4)

После вычисления резервов времени определяется критический путь , то есть полный путь, имеющий наибольшую продолжительность

. (1.5)

Для него является характерным, что все события, принадлежащие ему, не имеют резервов времени (они равны нулю). При поиске критических путей следует помнить, что признаком критической работы являются нулевые значения резервов времени. Это означает, что каждая последующая критическая работа будет начинаться строго в момент окончания предыдущей критической работы.

Вследствие этого сдвиг любой из работ критического пути обязательно приведет к увеличению первоначальной длительности проекта (ТКР). Кроме того, следует учесть, что критический путь является полным, т. е. соединяет исходное и завершающее события сети.

Поэтому первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.

1.6 Пример построения сетевого графика

На предприятии осуществляется реконструкция цеха. Известна средняя продолжительность выполнения отдельных работ (см. таблицу 1.1). Среднеквадратическое отклонение продолжительности выполнения работ sn (где n – номер работы) по всем работам комплекса равно одному дню.

Необходимо:

1.  Построить сетевой график выполнения работ по реконструкции цеха и определить значения его параметров (ранние и поздние сроки событий, начала и окончания работ, резервы времени по отдельным событиям, полные резервы времени по отдельным работам).

2.  Определить на сетевом графике критический путь и среднее время выполнения работ по реконструкции цеха. Критический путь выделить отдельной линией и отдельно дать перечень работ, принадлежащих критическому пути и его длительность.

РЕШЕНИЕ:

Таблица 1.1. – Исходные данные для решения задания 1

1. Определяем ранние сроки наступления события

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6