Эконометрика и экономико-математические методы и модели (стр. 2 )

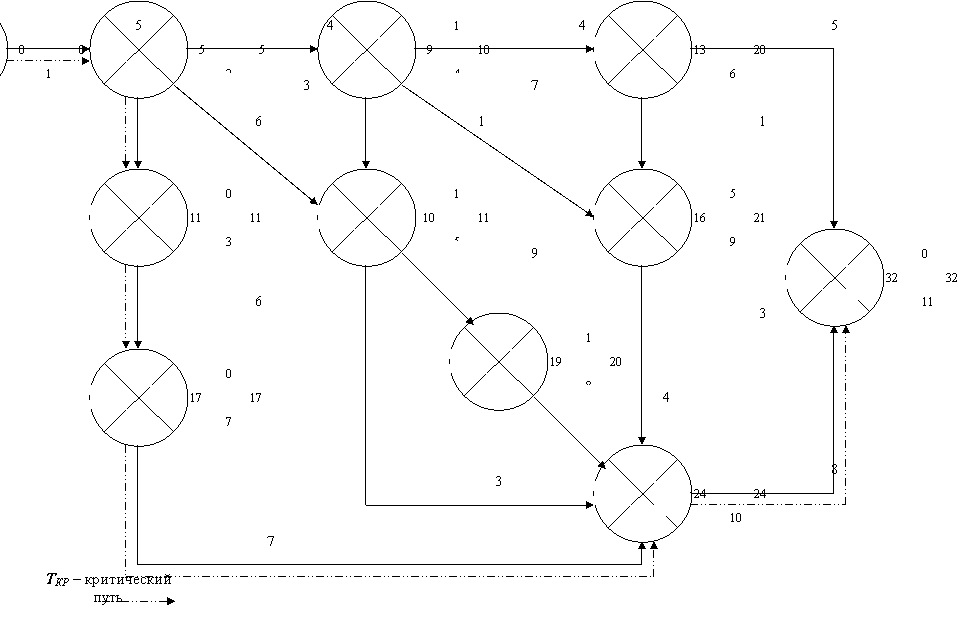
Используя формулу (1.1) рассчитаем ранние сроки свершения события

, i = 1, 2, …, k,

где ТPj – ранний срок наступления j-го события;

ТPi – ранний срок наступления i-го события;

tij – срок средней продолжительности работы ij;

k – число работ, предшествующих i-му событию (все эти работы на сетевом графике обозначаются стрелками, входящими в кружок, обозначающий j-e событие).

;

;

;

;

;

;

;

;

;

.

2. Определяем поздние сроки наступления события

Используя формулу (1.2) рассчитаем поздние сроки свершения события

, j = 1, 2, …, L,

где ТПi – поздний срок наступления i-го события;

ТПj – поздний срок наступления j-го события;

tij – срок средней продолжительности работы ij;

L – число работ, непосредственно следующих за i-м событием (все эти работы на сетевом графике обозначаются стрелками, выходящими из кружка, обозначающего i-ое событие).

;

;

;

;

;

;

;

;

;

.

3. Определяем резервы времени

Используя формулу (1.3) рассчитаем резервы времени по отдельным событиям

.

Критический путь проходит через события, где полный резерв времени равен 0.

; *

; *

; *

;

;

;

; *

;

;

; *

. *

Таким образом, критический путь проходит через события:

1) 11.

4. Определяем полный резерв времени

Используя формулу (1.4) рассчитаем полные резервы времени по отдельным работам

.

Критический путь проходит через работы, где полный резерв времени равен 0.

; *

; *

;

;

; *

;

;

;

;

;

;

;

; *

;

;

. *

5. Найдем длину критического пути.

Используя формулу (1.5) рассчитаем длительность критического пути

,

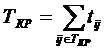ВЫВОД: Таким образом, критическим путем является путь, проходящий через события 11 и его продолжительность (длительность) составляет 32 дня.

2 ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ.

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

2.1 Роль корреляционно-регрессионного анализа в обработке экономических данных

Обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности. Вообще говоря, трудно назвать ту сферу, в которой она бы не использовалась. Но, пожалуй, ни в одной области знаний и практической деятельности обработка статистических данных не играет такой исключительно большой роли, как в экономике, имеющей дело с обработкой и анализом огромных массивов информации о социально-экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимает корреляционный и регрессионный анализы обработки статистических данных.

В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и регрессионного анализа. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и не только выявить, но и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под причинной зависимостью понимается такая связь между процессами, когда изменение одного из них является следствием изменения другого.

Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом.

Использование возможностей современной вычислительной техники, оснащенной пакетами программ машинной обработки статистической информации на ЭВМ, делает практически осуществимым оперативное решение задач изучения взаимосвязи показателей методами корреляционно-регрессионного анализа.

При машинной обработке исходной информации на ЭВМ, оснащенных пакетами стандартных программ ведения анализов, вычисление параметров, применяемых математических функций, является быстро выполняемой счетной операцией.

Корреляционный анализ и регрессионный анализ являются смежными разделами математической статистики и предназначаются для изучения по выборочным данным статистической зависимости ряда величин; некоторые из которых являются случайными. При статистической зависимости величины не связаны функционально, но как случайные величины заданы совместным распределением вероятностей. Исследование взаимосвязи случайных величин показателей приводит к теории корреляции, как разделу теории вероятностей, и корреляционному анализу, как разделу математической статистики. Исследование зависимости случайных величин приводит к моделям регрессии и регрессионному анализу на базе выборочных данных. Теория вероятностей и математическая статистика представляют лишь инструмент для изучения статистической зависимости, но не ставят своей целью установление причинной связи. Представления и гипотезы о причинной связи должны быть привнесены из некоторой другой теории, которая позволяет содержательно объяснить изучаемое явление.

Экономические данные почти всегда представлены в виде таблиц. Числовые данные, содержащиеся в таблицах, обычно имеют между собой явные (известные, или же связи первого типа) или неявные (скрытые, или же связи второго типа) связи.

Явно связаны показатели, которые получены методами прямого счета, т. е. вычислены по заранее известным формулам. Например, проценты выполнения плана, уровни, удельные веса, отклонения в сумме, отклонения в процентах, темпы роста, темпы прироста, индексы и т. д.

Связи же второго типа (неявные) заранее неизвестны. Однако необходимо уметь объяснять и предсказывать (прогнозировать) сложные явления для того, чтобы управлять ими. Поэтому специалисты с помощью наблюдений стремятся выявить скрытые зависимости и выразить их в виде формул, т. е. математически смоделировать явления или процессы. Одну из таких возможностей предоставляет корреляционно-регрессионный анализ.

Математические модели строятся и используются для трех обобщенных целей:

Ø  для объяснения;

Ø  для предсказания;

Ø  для управления.

Представление экономических и других данных в электронных таблицах в наши дни стало простым и естественным. Оснащение же электронных таблиц средствами корреляционно-регрессионного анализа способствует тому, что из группы сложных, глубоко научных и потому редко используемых, почти экзотических методов, корреляционно-регрессионный анализ превращается для специалиста в повседневный, эффективный и оперативный аналитический инструмент. Однако, в силу его сложности, освоение его требует значительно больших знаний и усилий, чем освоение простых электронных таблиц.

Пользуясь методами корреляционно-регрессионного анализа, аналитики измеряют тесноту связей показателей с помощью коэффициента корреляции. При этом обнаруживаются связи, различные по силе (сильные, слабые, умеренные и др.) и различные по направлению (прямые, обратные). Если связи окажутся существенными, то целесообразно будет найти их математическое выражение в виде регрессионной модели и оценить статистическую значимость модели. В экономике значимое уравнение используется, как правило, для прогнозирования изучаемого явления или показателя.

Регрессионный анализ называют основным методом современной математической статистики для выявления неявных и завуалированных связей между данными наблюдений. Электронные таблицы делают такой анализ легко доступным. Таким образом, регрессионные вычисления и подбор хороших уравнений – это ценный, универсальный исследовательский инструмент в самых разнообразных отраслях деловой и научной деятельности (экономика, маркетинг, торговля, медицина и т. д.). Усвоив технологию использования этого инструмента, можно применять его по мере необходимости, получая знание о скрытых связях, улучшая аналитическую поддержку принятия решений и повышая их обоснованность.

Корреляционно-регрессионный анализ считается одним из главных методов в экономике, наряду с оптимизационными расчетами, а также математическим и графическим моделированием трендов (тенденций). Широко применяются как однофакторные, так и множественные регрессионные модели.

2.2 Корреляционно-регрессионный анализ: понятие, его возможности, предпосылки

Корреляционный анализ является одним из методов статистического анализа взаимосвязи нескольких признаков.

Он определяется как метод, применяемый тогда, когда данные наблюдения можно считать случайными и выбранными из генеральной совокупности, распределенной по многомерному нормальному закону. Основная задача корреляционного анализа (являющаяся основной и в регрессионном анализе) состоит в оценке уравнения регрессии.

Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

1. Парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными).

2. Частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.

3. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным признаком и множеством факторных признаков (при многофакторной связи).

Теснота связи количественно выражается величиной коэффициентов корреляции. Коэффициенты корреляции, представляя количественную характеристику тесноты связи между признаками, дают возможность определить «полезность» факторных признаков при построении уравнений множественной регрессии. Величина коэффициентов корреляции служит также оценкой соответствия уравнению регрессии выявленным причинно-следственным связям.

Первоначально исследования корреляции проводились в биологии, а позднее распространились и на другие области, в том числе на социально-экономическую. Одновременно с корреляцией начала использоваться и регрессия. Корреляция и регрессия тесно связаны между собой: первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму. И корреляция, и регрессия служат для установления соотношений между явлениями и для определения наличия или отсутствия связи между ними.

Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые данные. При этом полагают, что эти данные являются значениями случайной величины. Случайной величиной называется переменная величина, которая в зависимости от случая принимает различные значения с некоторой вероятностью. Закон распределения случайной величины показывает частоту ее тех или иных значений в общей их совокупности.

При исследовании взаимосвязей между экономическими показателями на основе статистических данных часто между ними наблюдается стохастическая зависимость. Она проявляется в том, что изменение закона распределения одной случайной величины происходит под влиянием изменения другой. Взаимосвязь между величинами может быть полной (функциональной) и неполной (искаженной другими факторами). Пример функциональной зависимости – выпуск продукции и ее потребление в условиях дефицита. Неполная зависимость наблюдается, например, между стажем рабочих и их производительностью труда. Обычно рабочие с большим стажем трудятся лучше молодых, но под влиянием дополнительных факторов – образование, здоровье и т. д. эта зависимость может быть искажена.

Раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами, называется корреляционным анализом (от лат. correlatio соотношение, соответствие). Основная задача корреляционного анализа – это установление характера и тесноты связи между результативными (зависимыми) и факторными (независимыми) показателями (признаками) в данном явлении или процессе. Корреляционную связь можно обнаружить только при массовом сопоставлении фактов. Характер связи между показателями определяется по корреляционному полю. Если Y зависимый признак, а Х независимый, то, отметив каждый случай Х(i) с координатами Xi и Yi, получим корреляционное поле. По расположению точек можно судить о характере связи (рис. 2.1).

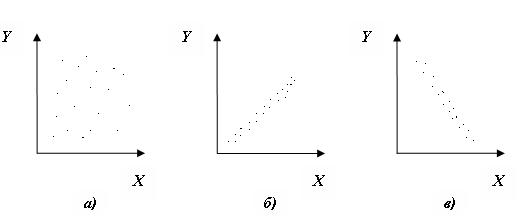
а) переменные X и Y не коррелируют;

б) наблюдается сильная положительная корреляция;

в) наблюдается слабая отрицательная корреляция.

Рисунок 2.1 – Примеры корреляционных полей

Теснота связи определяется с помощью коэффициента корреляции, который рассчитывается специальным образом и лежит в интервалах от минус единицы до плюс единицы. Если значение коэффициента корреляции лежит в интервале от 1 до 0,9 по модулю, то отмечается очень сильная корреляционная зависимость. В случае, если значение коэффициента корреляции лежит в интервале от 0,9 до 0,6, то говорят, что имеет место слабая корреляционная зависимость. Наконец, если значение коэффициента корреляции находится в интервале от -0,6 до 0,6, то говорят об очень слабой корреляционной зависимости или полном ее отсутствии.

Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами.

Регрессионный анализ своей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой или независимых переменных известна. Практически, речь идет о том, чтобы, анализируя множество точек на графике (т. е. множество статистических данных), найти линию, по возможности точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию), линию регрессии.

По числу факторов различают одно-, двух - и многофакторные уравнения регрессии.

По характеру связи однофакторные уравнения регрессии подразделяются на:

а) линейные:

, (2.1)

где х – экзогенная (независимая) переменная;

y – эндогенная (зависимая, результативная) переменная;

а, b – параметры.

б) степенные:

; (2.2)

в) показательные:

; (2.3)

г) прочие.

Перед рассмотрением предпосылок корреляционного и регрессионного анализа, следует сказать, что общим условием, позволяющим получить более стабильные результаты при построении корреляционных и регрессионных моделей показателей, является требование однородности исходной информации. Эта информация должна быть обработана на предмет аномальных, т. е. резко выделяющихся из массива данных, наблюдений. Эта процедура выполняется за счет количественной оценки однородности совокупности по какому-либо одномерному или многомерному критерию (в зависимости от исходной информации) и имеет цель тех объектов наблюдения, у которых наилучшее (или наихудшее) условия функционирования по не зависящим или слабо зависящим причинам.

После обработки данных на предмет «аномальности» следует провести проверку, насколько оставшаяся информация удовлетворяет предпосылкам для использования статического аппарата при построении моделей, так как даже незначительные отступления от этих предпосылок часто сводят к нулю получаемый эффект. Следует иметь ввиду, что вероятностное или статистическое решение любой экономической задачи должно основываться на подробном осмыслении исходных математических понятий и предпосылок, корректности и объективности сбора исходной информации, в постоянном сочетании с теснотой связи экономического и математико-статистического анализа.

Для применения корреляционного анализа необходимо, чтобы все рассматриваемые переменные были случайными и имели нормальный закон распределения. Причем выполнение этих условий необходимо только при вероятностной оценке выявленной тесноты связи.

Хотелось бы отметить, что наиболее сложным этапом, завершающим регрессионный анализ, является интерпретация полученных результатов, т. е. перевод их с языка статистики и математики на язык экономики.

Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относятся исследуемые явления. Всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков, т. е. с изучения, как они влияют на величину результативного признака. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемую обработку показателей. Особое значение при этом имеет знак перед коэффициентом регрессии. Знаки коэффициентов регрессии говорят о характере влияния на результативный признак статистической обработки показателей. Если факторный признак имеет плюс, то с увеличением данного фактора результативный признак возрастает; если факторный признак со знаком минус, то с его увеличением результативный признак уменьшается. Интерпретация этих знаков полностью определяется социально-экономическим содержанием моделируемого признака. Если его величина изменяется в сторону увеличения, то плюсовые знаки факторных признаков имеют положительное влияние. При изменении результативного признака в сторону снижения положительные значения имеют минусовые знаки факторных признаков. Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а он со знаком минус, то необходимо проверить расчеты параметров уравнения регрессии.

Корреляционный и регрессионный анализ позволяет определить зависимость между факторами, а также проследить влияние задействованных факторов. Эти показатели имеют широкое применение в обработке статистических данных для достижения наилучших показателей.

2.3 Пример проведения корреляционно-регрессионного анализа

Определить уравнение связи между производительностью труда и рентабельностью предприятия. Вычислить коэффициенты корреляции между производительностью труда и рентабельностью предприятия. Проверить гипотезу о значимости отличия коэффициента корреляции от нуля. Считая связь между производительностью труда и рентабельностью предприятия линейной, построить уравнение связи между названными показателями, используя метод наименьших квадратов. Проверить гипотезу об отличии от нуля коэффициента регрессии. Дать экономическую интерпретацию полученных результатов. Исходные данные приведены в таблице 2.1.

РЕШЕНИЕ:

Таблица 2.1 – Исходные данные для решения задания 2

I ЭТАП (решение задачи с помощью метода наименьших квадратов)

Исходные данные и промежуточные расчеты (результаты) удобно свести в таблицу 2.2.

Таблица 2.2 – Исходные данные и промежуточные результаты

; (2.4)

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6