Эконометрика и экономико-математические методы и модели (стр. 4 )

I ЭТАП (решение задачи с помощью симплекс-метода)

Составим экономико-математическую модель задачи.

Введем следующие обозначения:

Х1 – планируемый выпуск трикотажного полотна артикула 150 на машине Текстима (т);

Х2 – планируемый выпуск трикотажного полотна артикула 90 на машине Текстима (т);

Х3 – планируемый выпуск трикотажного полотна артикула 150 на машине Кокетт (т);

Х4 – планируемый выпуск трикотажного полотна артикула 90 на машине Кокетт (т).

Составим целевую функцию, выражающую прибыль, получаемую от выпуска всей продукции

.

Составим ограничения на фонд машинного времени имеющегося оборудования

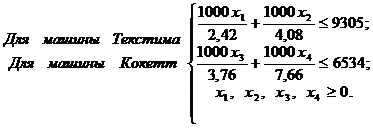
Для того чтобы решить задачу симплекс-методом, нужно ограничения неравенств преобразовать в равенство.

В первое ограничение добавим положительную величину х5.

Во второе ограничение добавим положительную величину х6.

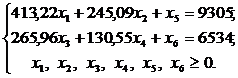
Так как неизвестные х5 и х6 выражают неиспользуемое время работы соответствующего оборудования и следовательно, не влияют на прибыль, то в целевую функцию эти неизвестные входят с нулевыми коэффициентами

.

В результате получим математическую модель, представляющую общую задачу линейного программирования.

Решим задачу симплекс-методом.

Преобразуем целевую функцию:

алгоритм симплекс-метода

;

;

.

Этапы задачи оформлены в виде симплекс-таблицы (см. таблицу 3.3).

Таблица 3.3 – Симплекс-таблица

Чтобы получить первую строчку второй таблицы, переписываем первую строчку первой таблицы. Для того чтобы получить вторую строчку второй таблицы, делим вторую строчку первой таблицы на 265,96. Чтобы получить третью строчку второй таблицы, нужно вторую строчку второй таблицы умножить на 13,46 и вычесть из третьей строчки первой таблицы.

Чтобы получить первую строчку третьей таблицы, делим первую строчку второй таблицы на 413,22. Чтобы получить вторую строчку третьей таблицы, переписываем вторую строчку второй таблицы. Чтобы получить третью строчку третьей таблицы, нужно первую строчку третьей таблицы умножить на 13,4 и вычесть из третьей строчки второй таблицы.

Чтобы получить первую строчку четвертой таблицы, переписываем первую строчку третьей таблицы. Чтобы получить вторую строчку четвертой таблицы, делим вторую строчку третьей таблицы на 0,49. Чтобы получить третью строчку четвертой таблицы, умножаем вторую строчку четвертой таблицы на 0,57 и вычитаем из третьей строки третьей таблицы.

В результате в четвертой симплекс-таблице получили в строке –L все коэффициенты £ 0. Значит план оптимальный и задача решена.

Х1 = 22,52 т – выпуск трикотажного полотна артикула 150 на машине текстима;

Х2 = 0 т – выпуск трикотажного полотна артикула 90 на машине текстима;

Х3 = 0 т – выпуск трикотажного полотна артикула 150 на машине кокетт;

Х4 = 50,14 т – выпуск трикотажного полотна артикула 90 на машине кокетт;

Х5 = 0 т – дополнительно вводимая положительная величина;

Х6 = 0 т– дополнительно вводимая положительная величина.

тыс. руб. – прибыль общая, получаемая от реализации всех видов изделий.

,

т. е. для получения максимальной прибыли 661,06 тыс. руб. трикотажной фабрике необходимо выпускать:

– трикотажного полотна артикула 150 на машине текстима в объеме 22,52 т;

– трикотажного полотна артикула 90 на машине текстима не выпускать;

– трикотажного полотна артикула 150 на машине кокетт не выпускать;

– трикотажного полотна артикула 90 на машине кокетт выпускать в объеме 50,14 т.

Проведем анализ использования оборудования

Машина текстима используется для выпуска 22,52 т полотна артикула 150; полотно артикула 90 на машине не выпускается, следовательно, будет затрачено

,

и фонд рабочего времени машины текстима будет использоваться сверхустановленного лимита, т. к.

– будет использоваться сверхустановленного лимита.

Машина кокетт используется для выпуска 50,14 т полотна артикула 90, а полотно артикула 150 на машине кокетт не выпускается, следовательно, будет затрачено

,

и фонд рабочего времени машины кокетт будет использоваться сверхустановленного лимита, т. к.

– будет использоваться сверхустановленного лимита.

Ответ: Таким образом, для получения максимальной прибыли, равной 661,06 тыс. руб., трикотажной фабрике рекомендуется выпускать 22,52 т трикотажного полотна артикула 150 на машине текстима и 50,14 т трикотажного полотна артикула 90 на машине кокетт. Остальные виды продукции не производить. При этом имеющийся фонд рабочего времени машины текстима будет использоваться сверхустановленного лимита на 1 маш/час., а фонд рабочего времени машины кокетт будет использоваться сверхустановленного лимита на 12 маш/час.

II ЭТАП (решение задачи с помощью утилиты «Поиск решения»)

Прикладной программный продукт ТП Excel фирмы Microsoft содержит в своем составе достаточно мощное средство для решения задач оптимизации с учетом ограничений. Это так называемая утилита «Поиск решения» (см. рисунок 3.1). Прокомментируем некоторые аспекты работы с этой утилитой.

Рисунок 3.1 – Окно утилиты «Поиск решения»

Искомые переменные – ячейки рабочего листа Excel – называются регулируемыми ячейками.

Целевая функция L(х1, х2, ..., хn), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:

– найти максимум целевой функции L(х1, х2, ..., хn);

– найти минимум целевой функции L(х1, х2, ..., хn);

– добиться того, чтобы целевая функция L(х1, х2, ..., хn) имела фиксированное значение: L(х1, х2, ..., хn) = а.

Функции G(х1, х2, ..., хn) называются ограничениями. Их можно задать как в виде равенств, так и неравенств.

На регулируемые ячейки (искомые параметры – х1, х2, ..., хn) можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда решение ищется в области положительных и/или целых чисел.

Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования.

Управление диалоговым окном утилиты «Поиск решения» (см. рисунок 3.1) осуществляется следующим образом:

1.  установить целевую ячейку – служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу для вычисления целевой функции;

2.  равной – служит для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор заданного числа). Чтобы установить число, его необходимо ввести в поле;

3.  изменяя ячейки – служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле «Установить целевую ячейку». В этих ячейках должны содержаться переменные оптимизационной модели;

4.  ограничения – служат для отображения списка граничных условий поставленной задачи;

5.  выполнить – служит для запуска поиска решения поставленной задачи.

«Поиск решения» позволяет представить результаты в виде трех отчетов: Результаты, Устойчивость и Пределы.

Для генерации одного или нескольких отчетов выделяются их названия в окне диалога «Результаты» утилиты «Поиск решения».

Отчет по устойчивости содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений.

Отчет по результатам содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй – значения искомых переменных, полученные в результате решения задачи, в третьей – результаты оптимального решения для ограничений. Кроме того, содержится информация о параметрах каждого ограничения: статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы – это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения.

Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи.

Постановка задачи в терминах рабочего листа Excel для использования утилиты «Поиск решения».

1.  Разместим исходные данные на листе MS Excel.

2.  В окне «Поиск решения» зададим целевую ячейку, изменяемые ячейки и ограничения (рисунок 3.2).

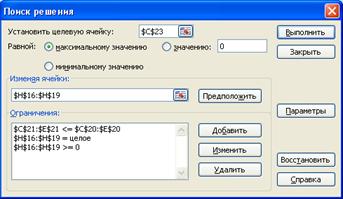
Рисунок 3.2 – Окно утилиты «Поиск решения» задачи

В приложениях 4, 5, 6, 7, 8 представлены результаты работы утилиты «Поиск решения».

Таким образом, для получения максимальной прибыли, равной 660,60 тыс. руб., трикотажной фабрике рекомендуется выпускать 22,52 т трикотажного полотна артикула 150 на машине текстима и 50,05 т трикотажного полотна артикула 90 на машине кокетт. Остальные виды продукции не производить. При этом имеющиеся фонды рабочего времени машин текстима и кокетт будут использованы полностью.

4 ВАРИАНТЫ ЗАДАЧ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

4.1 СЕТЕВЫЕ МОДЕЛИ.

СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ

На предприятии осуществляется реконструкция цеха. Известна средняя продолжительность выполнения отдельных работ (см. таблицу 4.1). Среднеквадратическое отклонение продолжительности выполнения работ sn (где n – номер работы) по всем работам комплекса равно одному дню.

Необходимо:

3.  Построить сетевой график выполнения работ по реконструкции цеха и определить значения его параметров (ранние и поздние сроки событий, начала и окончания работ, резервы времени по отдельным событиям).

4.  Определить на сетевом графике критический путь и среднее время выполнения работ по реконструкции цеха. Критический путь выделить отдельной линией и отдельно дать перечень работ, принадлежащих критическому пути и его длительность.

Таблица 4.1 – Исходные данные для выполнения задания 1

Продолжение таблицы 4.1

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6