На правах рукописи
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-
СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра физика
ИЗУЧЕНИЕ СПЕКТРА ВОДОРОДА
Методические указания к лабораторной работе №50
Волгоград 2010
УДК 537
Изучение спектра водорода: Методические указания к лабораторной работе / Сост. , ; ВолгГАСУ. – Волгоград, 2010. – 12 с.
Целями работы являются измерение длин волн линий видимой (бальмеровской) серии спектра излучения атомарного водорода и расчёт постоянной Ридберга, массы и радиусов боровских орбит электрона. Приводится краткая теория Бора строения и оптических свойств атома водорода. Приведены описание экспериментальной установки, порядок выполнения работы, способы расчёта результатов измерений, сформулированы задания для учебно–исследовательской работы (УИРС).
Для студентов всех специальностей по дисциплине «Физика».
Ил. 6 Табл.3 Библиогр. 2 назв.
Составление , ,2010
Цели работы – измерение длин волн линий видимой (бальмеровской) серии спектра излучения атомарного водорода и расчёт постоянной Ридберга, массы и радиусов боровских орбит электрона.
Приборы и принадлежности: монохроматор – спектрометр УМ – 2, конденсор, источники света – ртутная лампа и водородная трубка, блок питания генератора и пульт управления.
Теоретическое введение.
На основании результатов опытов, проведённых Резерфордом, Гейгером
и Марсденом в 1911г. по рассеянию альфа–частиц тонкими металлическими фольгами, была предложена атомная модель атома.
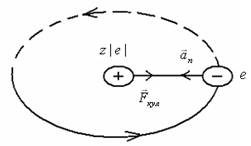 |
Согласно этой, так называемой планетарной модели Резерфорда, атом любого химического элемента состоит из положительно заряженного ядра, вокруг которого по круговым или эллиптическим орбитам вращаются электроны, масса которых составляет малую долю массы ядра. Линейные размеры ядра порядка (10–14 ÷10–15) м. Заряд ядра Qяд.= Z|е|, где Z – порядковый номер химического элемента в периодической системе Менделеева, |е| – модуль заряда электрона.
Рис.1. Кулоновское взаимодействие электрона и ядра атома
Предполагая ( рис. 1) что на электрон, равномерно вращающийся по орбите радиусом r ≈10–10 м (размер атома), со стороны ядра атома водорода (Z = 1) действует кулоновская сила
|![]() , (1)
, (1)
где ε0 – электрическая постоянная, из второго закона Ньютона:
![]() , (2)
, (2)
где m – масса покоя электрона, можно получить численное значение нормального ускорения an ≈ 1022 м/с2.
С точки зрения классической электродинамики такой ускоренно движущийся электрон должен вести себя как вибратор, колеблющийся с большой частотой, и излучающий электромагнитные волны. Согласно классическим представлениям, это излучение, и связанная с ним потеря электроном его энергии, должны происходить непрерывно. Поэтому электрон не сможет удержаться на круговой орбите – он должен по спирали приблизиться к ядру и частота его обращения вокруг ядра, а, следовательно, и частота излучаемых им электромагнитных волн, должны непрерывно изменяться. Иными словами, электромагнитное излучение атома должно иметь непрерывный, а не линейчатый спектр.
В действительности оказывается, что атом является устойчивой системой, излучающей при определённых условиях линейчатый спектр, связанный со строением и свойствами его электронной оболочки.
Для исключения этих существенных недостатков модели Резерфорда, Бор в 1913 г. предложил теорию, в основе которой лежала идея связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель Резерфорда и квантовый характер излучения и поглощения света, подтверждённые детальными экспериментальными исследованиями.
Теория Бора базируется на так называемых постулатах.
Первый постулат (стационарных состояний) – существуют некоторые стационарные состояния атома, находясь в которых, он не излучает энергии.
Этим стационарным состояниям соответствуют вполне определённые (стационарные) орбиты, по которым движутся электроны. При движении по стационарным орбитам электроны, несмотря на наличие у них ускорения, не излучают электромагнитных волн.
Рис.2. Орбитальный момент импульса электрона на n– ой боровской орбите
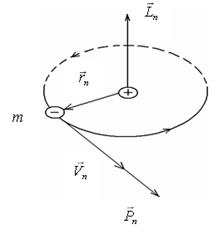 |
Второй постулат (квантования орбит) – в стационарном состоянии атома электрон, вращаясь по орбите, должен иметь значения момента импульса ( рис. 2 ), кратные приведённой постоянной Планка ħ
![]() ħ, (3)
ħ, (3)
где n – главное квантовое число, номер орбиты; n = 1, 2, 3 …; ħ ![]() ; h – постоянная Планка. Значение Ln можно определить следующим образом
; h – постоянная Планка. Значение Ln можно определить следующим образом
![]() , (4)
, (4)
где rn, Vn, Pn соответственно радиус n – ой орбиты, линейная скорость и импульс электрона на этой орбите.
Третий постулат (переходов или частот) – при переходе атома из одного стационарного состояния в другое испускается или поглощается один квант энергии, численное значение которого можно определить по формуле
![]() ħωnm, (5)
ħωnm, (5)
где Еn, Еm – соответственно полная энергия атома в n – и m – состояниях; ωnm = 2πvnm – циклическая частота перехода.
При Еn>Еm происходит излучение кванта, а при Еn<Еm – его поглощение.
Объединяя формулы (1), (2) (рис.1) и учитывая, что 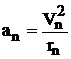 , получаем
, получаем 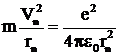 . После сокращения на rn и m выражаем
. После сокращения на rn и m выражаем ![]()
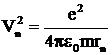 . (6)
. (6)
Объединяя формулы (З), (4) и возводя правые и левые их части в квадрат, получаем
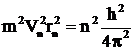 . (7)
. (7)
Подставляя (6) в (7), выражаем rn
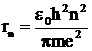 . (8)
. (8)
Формула (8) позволяет рассчитать радиусы боровских орбит электрона. Полная энергия электрона, находящегося на n–ой орбите (Еn), равна сумме его кинетической Кn и потенциальной Пn энергий
![]() . (9)
. (9)
Используя формулу (6)‚ определяем кинетическую энергию электрона
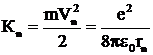 .
.
Поэтому кинетическую энергию электрона можно определить по формуле
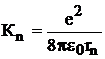 . (10)
. (10)
Потенциальная энергия электрона в электрическом поле ядра определяется по формуле
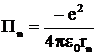 . (11)
. (11)
Подставляя (10) и (11) в (9), получаем полную энергию электрона
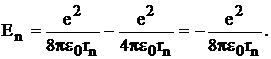
Поэтому полную энергию электрона можно определить по формуле
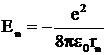 . (12)
. (12)
Подставляя формулу (8) в (12), определяем полную энергию электрона с учётом главного квантового числа n
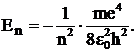 (13)
(13)
Из формулы (13) следует, что n определяет полную энергию электрона, находящегося в n– ом стационарном состоянии (поэтому n называют главным квантовым числом).
Согласно постулату переходов (или частот), атом излучает квант энергии частотой υnm, при переходе из n в m (n>m)
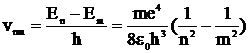 , или
, или 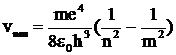 . (14)
. (14)
Разделив правую и левую части (14) на с – скорость света в вакууме, получим формулу Бальмера
![]() (15)
(15)
где n – номер орбиты, на которую электрон переходит; m – номер орбиты, с которой электрон переходит, m=n+1; 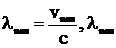 – длина волны, соответствующая излучаемому кванту; R – постоянная Ридберга, определяемая по формуле
– длина волны, соответствующая излучаемому кванту; R – постоянная Ридберга, определяемая по формуле
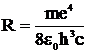 . (16)
. (16)
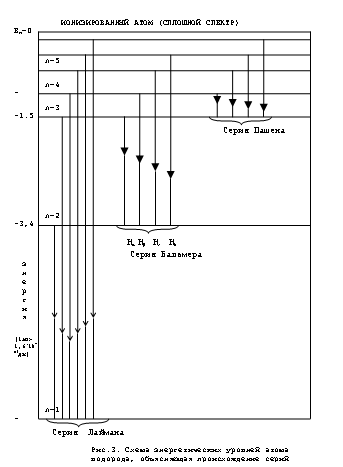
Из формулы Бальмера следует, что спектр излучения атома водорода состоит из дискретных линий, объединённых в группы или серии. Серия – это совокупность спектральных линий, описываемых формулой (15) при n=const, рис. 3.
При переходе электронов на орбиту с минимальной энергией (n=1 – основное состояние), образуется серия Лаймана, лежащая в далёкой ультрафиолетовой части спектра. Если переход осуществляется на орбиту с n=2, излучается серия Бальмера, четыре из девяти линий которой лежат в видимой части спектра. Переход на орбиту с n=3 порождает серию Пашена, лежащую в инфракрасной (ИК) части спектра. Серии Брэкета (n=4), Пфунда (n=5) и Хэмфри (n=6) лежат в далекой ИК области спектра. Таким образом, теория Бора позволяет объяснить возникновение спектра излучения и рассчитать длины (или частоты линий) в спектре водорода. Однако она не позволяет объяснить различия интенсивностей линий в спектре излучения водорода и закономерности возникновения спектров излучения более сложных атомов. Эти трудности успешно преодолеваются современной квантовой теорией, показавшей неприемлемость классических представлений к микрообъектам.
МЕТОД ИЗМЕРЕНИЯ
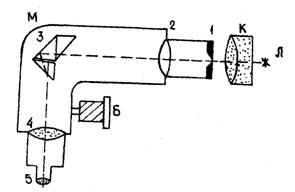 |
Установка для исследования спектров состоит из монохроматора-спектрометра УМ–2 (М, рис. 4), конденсора К, источников света Л – ртутной лампы или водородной трубки, генератора и пульта управления (на схеме не показаны).
Рис.4. Принципиальная схема установки для наблюдения и измерения длин волн линий спектров излучения различных газов
Свет от включённого источника Л проходит через конденсорную линзу К, входную щель монохроматора 1, коллиматорную линзу 2, и разлагается в спектр призмой 3, установленной на поворотном столике, который вращается на вертикальной оси при помощи микрометрического винта с отчётным барабаном Б. С помощью линзы 4 спектр исследуется визуально в её фокальной плоскости посредством окуляра 5. На барабан нанесена винтовая дорожка с градусными делениями. Вдоль дорожки скользит указатель поворота барабана. При вращении барабана поворачивается призма 3, и в центре поля зрения появляются различные участки спектра.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1. Градуировка установки – снятие кривой зависимости показаний барабана монохроматора от длины волны излучения ртутной лампы.
1. Определите цену деления барабана монохроматора.
2. Включите вилку шнура блока питания в розетку, расположенную под рабочим столом на стояке, прикреплённом к полу.
3. Включите ртутную лампу – учтите, что она должна работать не более 7 минут. Для этого на пульте управления блоком питания (рис. 5) включите последовательно тумблеры Т1 и Т2 и затем сильно нажмите на кнопку К.
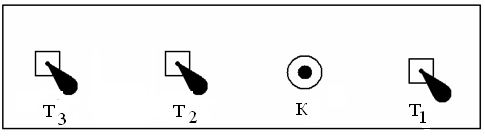
Рис.5. Передняя панель блока питания.
Т1– тумблер "вкл. – выкл." питания пульта управления;
Т2 и К – соответственно, тумблер и кнопка "вкл. – выкл." питания ртутной лампы;
тумблер Т3 – "вкл. – выкл." питания водородной трубки.
4. Вращая барабанчик окуляра 5 (рис. 4), добейтесь максимальной резкости наблюдения линий спектра, например, проверьте разделения дублета (двух) жёлтых линий – №№ 3и 4 в таблице 1.
5. С помощью барабана монохроматора установите против указателя крайнюю левоотстоящую красную линию – цветная вклейка в настольном варианте.
6. Для отсчёта положения линии её центр совмещайте с острием указателя. Отсчёт производите по делениям барабана относительно тёмной риски на указателе поворота барабана. Положение каждой линии промеряйте три раза. Для этого, получив первое измерение положения линии, поверните барабан вправо или влево и повторите измерение. Для наблюдения самых слабых линий в крайней, правоотстоящей, фиолетовой области спектра, слегка поворачивайте барабан в обе стороны от среднего положения линии, поскольку глаз лучше замечает слабые линии в движении.
7. Результаты последовательных (слева–направо) измерений положения линий спектра занесите в таблицу 1.
8. Выключите ртутную лампу. Для этого последовательно отключите тумблеры Т2 и Т1.
9. По результатам таблицы 1 постройте градуировочный график. По горизонтальной оси отложите длины волн li в Å, по вертикальной оси – соответствующие положения барабана (φi)ср. в градусах. Соедините полученные точки плавной кривой.
Таблица 1
Градуировка установки по спектру излучения ртутной лампы
λi,Å φi град | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
6907 | 6123 | 5791 | 5770 | 5461 | 4916 | 4358 | 4078 | 4047 | |
φ1 | |||||||||
φ2 | |||||||||
φ3 | |||||||||
(φi )ср. |
Задание 2. Изучение спектра излучения водородной трубки – определение длин волн видимой части серии Бальмера.
Переведите барабан монохроматора в положение, соответствующее среднему расположению красных линий спектра излучения ртутной лампы. В спектре водорода первая линия максимальной интенсивности Hα (красная), вторая – Hβ (зелёно–голубая), Hγ – фиолетово–синяя, Hδ – фиолетовая (очень слабая).
1. Включите водородную трубку, последовательно задействовав тумблеры Т1 и Т3.
2. Выполните действия, описанные в п. п. 5, 6 первого задания и занесите результаты измерений в таблицу 2. Учтите, во–первых, что измерению подлежат только линии, появляющиеся при включении тумблера Т3 и исчезающие при его отключении (так называемые «паразитные» линии, обусловленные солнечным светом, или лампами дневного света, наблюдаются и без включения блока питания). Во–вторых, спектр водорода снимается при выключенной ртутной лампе, поэтому в поле зрения будет видна центральная линия на фоне темноты и молоразличимого указателя монохроматора. Фиксируйте показания барабана в момент появления узкой тёмной полоски указателя монохроматора на середине спектральной линии.
3. Тумблерами Т1 и Т3 отключите водородную трубку и питание пульта управления и выдерните вилку шнура блока питания из розетки сети.
Таблица 2
Определение длин волн видимой части серии Бальмера
Обозначение линии φi, град | Hα | Hβ | Hγ | Hδ |
φ1 | ||||
φ2 | ||||
φ3 | ||||
(φi )ср. | ||||
λi, Å (по графику) | ||||
mi (ф.(15)) | 3 | 4 | 5 | 6 |
4.
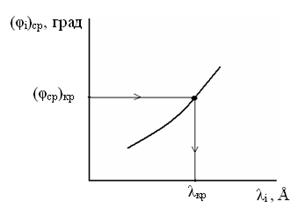 |
По построенному градуировочному графику определите длины волн в спектре водорода и занесите в таблицу 2. Определив значение (φi) ср. на вертикальной оси, проведите перпендикуляр на градуировочную кривую, а из точки пересечения опустите перпендикуляр на горизонтальную ось, точка пересечения определит значение λi соответствующей линии (рис. 6).
Рис.6. Определение длин волн линий спектра водорода по градуировочному графику
Задание 3. Вычисление постоянной Ридберга, а также массы, радиуса боровской орбиты и длины волны де–Бройля электрона, находящегося на первой орбите атома водорода.
1. Определите постоянную Ридберга
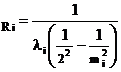
для mi = 3, 4, 5, 6 соответствующих видимым линиям спектра. Значения li переведите в м, учитывая, что 1Å=10–10 м. Определите среднее значение Rср. и сравните его с табличным.
2. Используя найденное среднее значение Rср., вычислите массу электрона
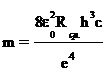 .
.
3. Вычислите радиус n –ой боровской орбиты электрона
![]() ,
,
где n = 1.
4. Определите длину волны де–Бройля для электрона, находящегося на n–ой орбите
![]() ,
,
где n = 1.
5. Используя найденное значение λБ, вычислите длину n –ой боровской орбиты электрона
Ln = 2prn,
где n = 1.
6. Определите число полуволн де–Бройля, укладывающихся на n – ой боровской орбите электрона
n = Ln / λБ.
Значения физических констант.
h ≈ 6,63∙10–34 Дж∙с; с ≈ 3∙108 м/с;
|е| ≈ 1,6∙10–19 Кл; ε0 ≈ 8,85∙10–12 Ф/м.
Таблица3
Значения постоянной Ридберга, массы электрона, радиуса первой боровской орбиты и длины волны де – Бройля электрона в атоме водорода.
Rα , м -1 | Rβ , м -1 | Rγ , м -1 | Rδ , м -1 | Rср., м -1 |
mэл., кг | r1, м | λБ, м | Ln, м | n |
ЗАДАНИЕ К УИРС
1. По указанию преподавателя выполните задания 1 и 2 (п. п. 1 – 5) для спектров излучения гелия, неона и других газов, занеся в соответствующим образом изменённую таблицу 2 значения показаний барабана, длин волн, цвет и сравнительную интенсивность (слабая, средняя, яркая) каждой линии.
2. Проанализируйте полученные Вами характеристики спектров с табличными.
3. Выполните виртуальную лабораторную работу №3.2 «Спектр излучения атомарного водорода» в обучающей компьютерной программе «Открытая физика 1.1»
ТЕХНИКА БЕЗОПАСНОСТИ
1. Перед началом работы убедитесь в исправности соединительных проводов, вилок, розеток. При обнаружении неисправностей обратитесь к преподавателю.
2. Во избежание ожогов не прикасайтесь к кожуху работающей ртутной лампы.
3. Не держите руку на коробке подключённого к сети блока питания.
4. Во избежание усталости глаз, чередуйте измерения с краткими перерывами, во время которых адаптируйте Ваше зрение «на бесконечность», например, посмотрите на небо.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Опишите модель атома по Резерфорду.
2. Перечислите основные недостатки модели атома по Резерфорду.
3. Сформулируйте постулаты Бора.
4. Определите физический смысл символа n в математической записи постулата квантования орбит.
5. Выведите формулу, выражающую потенциальную энергию электрона в электростатическом поле ядра атома водорода.
6. Задача.
Определите изменение энергии атома при излучении им кванта света,
длиной волны λ=6563Å.
7. Запишите выражение, описывающее возможные длины волн в спектре излучения атома водорода.
8. Перечислите основные недостатки теории атома по Бору.
9. Какая серия спектра водорода исследуется в работе? Наблюдаются ли другие серии?
10. Что такое градуировочный график установки?
ЛИТЕРАТУРА
1. Трофимова физики: Учебное пособие для студ. вузов. – М.: Высш. шк., 2007. – 432с., §§ 208–214; 223–225.
2. , Яворский физики: Учеб. пособие для студ. втузов. – 5–е изд., стер. – М.: Издательский центр «Академия», 2005. – 720 с., Гл. 38, § § 38.1– 38.5 Гл. 39, § § 39.1– 39.4.



