– создание условий, при которых возможно экспериментирование (подбор объектов для экспериментального воздействия, устранение влияния случайных факторов);
– определение пределов измерений;
– систематическое наблюдение за ходом развития изучаемого явления в процессе эксперимента и точные описания фактов;
– проведение систематической регистрации измеряемых величин различными средствами и способами;
– создание повторяющихся ситуаций, изменение характера условий и перекрестные воздействия, создание усложненных ситуаций с целью подтверждения или опровержения ранее полученных данных;
– переход от эмпирического изучения к логическим обобщениям, к анализу и теоретической обработке полученного фактического материала.
Важным этапом подготовки к эксперименту является определение его целей и задач. Объем и трудоемкость исследований зависят от степени точности принятых средств измерений и глубины теоретических разработок. Чем чётче сформулирована теоретическая часть исследования, тем меньше объем эксперимента. Количество задач для конкретного эксперимента не должно быть слишком большим (как правило 3 – 4, максимально до 10).
Чтобы перед экспериментом выбрать варьируемые факторы, то есть установить основные и второстепенные характеристики, влияющие на исследуемый процесс, необходимо проанализировать расчетные (теоретические) схемы процесса. При этом используется метод ранжирования (см. подразд. 5.1). Основным принципом установления степени важности характеристики является ее роль в исследуемом процессе. Для этого процесс изучается в зависимости от какой-то одной переменной при остальных постоянных. Такой принцип проведения эксперимента оправдывает себя лишь в тех случаях, когда таких характеристик не более трех. Если же переменных величин много, целесообразен принцип многофакторного анализа.
При регистрации величин в ходе одного и того же процесса повторные отсчеты на приборах, как правило, неодинаковы. Отклонения объясняются различными причинами – неоднородностью свойств изучаемого тела, погрешностью приборов, субъективными особенностями экспериментатора и др. Чем больше случайных факторов, влияющих на опыт, тем больше расхождения значений, получаемых при измерениях. Это ведет к необходимости повторных измерений. Установление потребного минимального количества измерений имеет большое значение, поскольку дает возможность получения наиболее объективных результатов при минимальных затратах времени и средств. Оно должно обеспечить устойчивое среднее значение измеряемой величины, удовлетворяющее заданной степени точности.
Чтобы обосновать набор средств измерений (приборов), экспериментатор должен быть хорошо знаком с выпускаемой в стране измерительной аппаратурой (при помощи регулярно издающихся каталогов, по которым можно заказать те или иные средства измерений). Естественно, что в первую очередь следует использовать стандартные, серийно выпускаемые машины и приборы, работа на которых регламентируется официальными документами. В отдельных случаях возникает потребность в создании уникальных приборов, установок, стендов, машин для разработки темы. Для этих целей желательно использовать готовые узлы выпускаемых приборов или реконструировать существующие. Причем целесообразность изготовления нового оборудования должна быть тщательно обоснована как теоретическими расчетами, так и практическими соображениями.
Важным разделом методики является выбор методов обработки и анализа экспериментальных данных. Обработка данных сводится к систематизации всех значений, классификации, анализу. Результаты экспериментов должны быть сведены в удобочитаемые формы записи – таблицы, графики, формулы, позволяющие быстро сопоставлять и анализировать полученные результаты. Размерность всех параметров должна соответствовать единой системе физических величин. Особое внимание в методике должно быть уделено математическим методам обработки и анализу опытных данных, в том числе установлению эмпирических зависимостей, аппроксимации связей между варьируемыми характеристиками, установлению критериев и доверительных интервалов.
6.4 Метрологическое обеспечение
экспериментальных исследований
Ответственный момент при проведении любых экспериментов – установление точности измерений и погрешностей. Методы измерений должны базироваться на законах специальной науки метрологии – науки об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Основными компонентами метрологии являются:
– общая теория измерений; единицы физических величин (величины, которым по определению присвоено числовое значение, равное единице) и их системы (совокупность основных и производных единиц, образованная в соответствии с некоторыми принципами);
– методы и средства измерений;
– методы определения точности измерений;
– основы обеспечения единства измерений, при которых результаты измерения выражены в узаконенных единицах, а погрешности измерений известны с заданной вероятностью, что возможно при единообразии средств измерения (средства измерения должны быть проградуированы в узаконенных единицах и их метрологические свойства соответствовать нормам).
Основоположником метрологии как науки в нашей стране был Д. И. Менделеев, создавший в 1893 г. Главную палату мер и весов, которой проведена, в частности, большая работа по внедрению метрической системы в бывшем СССР.
Метрологическая служба Республики Беларусь связана со всей системой стандартизации в стране, так как обеспечивает достоверность, сопоставимость показателей качества, закладываемых в стандарты, дает методы определения и контроля таких показателей. Метрологическая служба представляет собой разветвленную сеть научных и контрольно-испытательных организаций, способных выполнять значительные работы как в научно-теоретическом, так и в прикладных аспектах точных измерений. В настоящее время всю работу по стандартизации и метрологии в стране возглавляет Государственный комитет по стандартизации, метрологии и сертификации при Совете министров Республики Беларусь (Госстандарт), задачами которого являются совершенствование системы стандартизации и метрологии, расширение масштабов их использования для повышения технического уровня и качества продукции всех отраслей народного хозяйства, укрепление и развитие государственной метрологической службы, стандартизация методов, средств измерений и др. В основу его деятельности положен закон Республики Беларусь «Об обеспечении единства измерений», принятый в 1995 году.
Важнейшие значения в метрологии отводятся средствам измерений и эталонам. Согласно стандарту РМГ 29-99 (Рекомендации межгосударственные по стандартизации «Метрология. Основные требования и определения»), измерение – это нахождение физической величины опытным путем с помощью специальных технических средств. Суть измерения составляет сравнение измеряемой величины с известной величиной, принятой за единицу (эталон). К эталонам относятся средства измерений (или комплекс средств измерений), обеспечивающих воспроизведение и хранение единицы с целью передачи ее размера нижестоящим средствам измерения.
Для проверки рабочих (технических) средств измерения, постоянно используемых непосредственно в исследованиях, применяют образцовые средства измерений. Передача размеров единиц от эталонов или образцовых средств измерений рабочим средствам осуществляется государственными и ведомственными метрологическими органами. Их деятельность обеспечивает единство измерений и единообразие средств измерений.
6.5 Использование в исследованиях единиц системы СИ.
Метрическая система единиц
Метрическая система единиц – это общее название международной десятичной системы единиц, основными единицами которой являются метр и килограмм. При некоторых различиях в деталях элементы системы одинаковы во всем мире. Метрическая система выросла из постановлений, принятых Национальным собранием Франции в 1791 и 1795 годах по определению метра как одной десятимиллионной доли участка земного меридиана от Северного полюса до экватора. Определяя метр как десятимиллионную долю четверти земного меридиана, создатели метрической системы стремились добиться инвариантности и точной воспроизводимости системы. За единицу массы они взяли грамм, определив его как массу одной миллионной кубического метра воды при ее максимальной плотности.
Международная комиссия по метру в 1872 году постановила принять за эталон длины «архивный» метр, который представлял собой линейку из сплава платины с десятью процентами иридия, поперечному сечению которой придана X-образная форма для повышения жесткости при изгибе. В канавке такой линейки была продольная плоская поверхность, и метр определялся как расстояние между центрами двух штрихов, нанесенных поперек линейки на ее концах, при температуре эталона, равной 0 °С. В 1875 году многие страны мира подписали соглашение о метре, и этим соглашением была установлена процедура координации метрологических эталонов для мирового научного сообщества через Международное бюро мер и весов и Генеральную конференцию по мерам и весам. Точно также члены Комиссии приняли за эталон массы массу цилиндра высотой и диаметром около 3,9 см, сделанного из того же платиноиридиевого сплава, что и эталон метра.
Международные прототипы эталонов длины и массы – метра и килограмма – были переданы на хранение Международному бюро мер и весов, расположенному в Севре – пригороде Парижа. Они были выбраны из значительной партии одинаковых эталонов, изготовленных одновременно. Другие эталоны этой партии были переданы всем странам-участницам в качестве национальных прототипов (государственных первичных эталонов), которые периодически возвращаются в Международное бюро для сравнения с международными эталонами.
Метрическая система была весьма благосклонно встречена учеными. Ее основными преимуществами оказались простота использования и независимость воспроизведения единиц измерения. Основываясь на элементарных законах физики, исследователи начали вводить новые единицы для разных физических величин, связывая их с единицами длины и массы метрической системы. Если в механике единицы измерения удалось согласовать, то в области электричества и магнетизма длительное время существовали несколько различных систем единиц.
Для устранения путаницы между ними в начале XX в. было выдвинуто предложение объединить практические электрические единицы с соответствующими механическими, основанными на метрических единицах длины и массы, и построить некую согласованную (когерентную) систему. В 1960 году XI Генеральная конференция по мерам и весам приняла единую Международную систему единиц (СИ), дала определение основных единиц этой системы и предписала употребление некоторых производных единиц, «не предрешая вопроса о других, которые могут быть добавлены в будущем». Тем самым впервые в истории международным соглашением была принята Международная система единиц, которая в настоящее время принята в качестве законной большинством стран мира.
Международная система единиц (СИ) представляет собой согласованную систему, в которой для любой физической величины предусматривается только одна единица измерения. Некоторым из единиц даны особые названия, примером может служить единица давления – паскаль, тогда как названия других образуются из названий тех единиц, от которых они произведены, например единица скорости – метр в секунду. В систему СИ входят 7 основных единиц измерения (метр, килограмм, секунда, кельвин, моль, ампер, кандела) и 2 дополнительные (радиан и стерадиан).
В настоящее время официальные определения основных и дополнительных единиц системы СИ таковы:
– метр (м) – это длина пути, проходимого в вакууме светом за 1/299 792 458 долю секунды;
– килограмм (кг) равен массе международного прототипа килограмма;
– секунда (с) – продолжительность 9 периодов колебаний излучения, соответствующего переходам между двумя уровнями сверхтонкой структуры основного состояния атома цезия-133;
– кельвин (К) равен 1/273,16 части термодинамической температуры тройной точки воды;
– моль равен количеству вещества, в составе которого содержится столько же структурных элементов, сколько атомов в изотопе углерода-12 массой 0,012 кг;
– ампер (А) – сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины с бесконечно малой площадью поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызывал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2·107 Н.
– кандела (кд), ранее называвшаяся свечой – это единица силы света в данном направлении источника, испускающего монохроматическое излучение частоты 540·1012 Гц, энергетическая сила светового излучения которого в этом направлении составляет 1/683 Вт/ср. Это примерно соответствует силе света спермацетовой свечи, которая когда-то служила эталоном.
– радиан (рад) равен плоскому углу между двумя радиусами окружности, длина дуги между которыми равна радиусу;
– стерадиан (ср) равен телесному углу с вершиной в центре сферы, вырезающему на ее поверхности площадь, равную площади квадрата со стороной, равной радиусу сферы.
Приведенные определения показывают, что в настоящее время все основные единицы системы СИ, кроме килограмма, выражаются через физические константы или явления, которые считаются неизменными и с высокой точностью воспроизводимыми. Например, метр определяется через скорость света. Его можно воспроизвести независимо в любой хорошо оборудованной лаборатории. С развитием лазерной техники подобные измерения весьма упростились, и их диапазон существенно расширился. Погрешность при этом не превышает одной миллиардной. Точно также секунда в соответствии может быть реализована в компетентной лаборатории с точностью порядка 10–12. Время и его обратная величина – частота – уникальны в том отношении, что их эталоны можно передавать по радио. Поэтому каждый человек может принимать сигналы точного времени и эталонной частоты.
Что же касается килограмма, то еще не найден способ его реализации с той степенью воспроизводимости, которая достигается в процедурах сравнения различных эталонов массы с международным прототипом килограмма. Такое сравнение можно проводить путем взвешивания на пружинных весах, погрешность которых не превышает 10–8.
С помощью основных и дополнительных единиц образуются все производные. Из них наиболее важное значение имеют единица силы – ньютон, единица энергии – джоуль и единица мощности – ватт. Ньютон определяется как сила, которая придает массе в один килограмм ускорение, равное одному метру за секунду в квадрате. Джоуль равен работе, которая совершается, когда точка приложения силы, равной одному ньютону, перемещается на расстояние один метр в направлении действия силы. Ватт – это мощность, при которой работа в один джоуль совершается за одну секунду.
7 ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ
7.1 Задачи и методы теоретического исследования
Теория – это учение, система научных принципов, идей, обобщающих практический опыт и отражающих закономерности природы, общества, мышления. Это также совокупность обобщенных положений, образующих науку или раздел какой-либо науки.
Теоретические исследования ставят своей целью выделение в процессе синтеза знаний существенных связей между исследуемым объектом и окружающей средой, объяснение и обобщение результатов эмпирического исследования, выявление общих закономерностей и их формализацию.
Теория проходит в своем развитии различные стадии от качественного объяснения и количественного измерения процессов до их формализации и в зависимости от стадии может быть представлена как в виде качественных правил, так и в виде математических уравнений (соотношений). Однако формирование теории не всегда связано с построением ее математического аппарата.
Задачами теоретического исследования являются:
– обобщение результатов исследования, нахождение общих закономерностей путем обработки и интерпретации опытных данных;
– расширение результатов исследования на ряд подобных объектов без повторения всего объема исследований;
– изучение объекта, недоступного для непосредственного исследования,
– повышение надежности экспериментального исследования объекта (обоснования параметров и условий наблюдения, точности измерений).
Теоретические исследования включают анализ физической сущности процессов и явлений, формулирование гипотезы исследования, построение (разработку) физической модели, проведение математического исследования, анализ теоретических решений, формулирование окончательных выводов. Если не удается выполнить математическое исследование, то рабочая гипотеза формулируется в словесной форме с привлечением графиков, таблиц и т. д.
Процесс проведения теоретических исследований состоит обычно из нескольких стадий.
Оперативная стадия включает проверку возможности устранения технического противоречия, оценку возможных изменений в среде, окружающей объект, а также анализ возможности переноса решения задачи из других отраслей знания, применения «обратного» решения (нельзя ли использовать решения задач, обратных данной, взяв их со знаком «минус») или использования «прообразов» природы.
В процессе второй – синтетической – стадии исследования определяется влияние изменения одной части объекта на построение других его частей, устанавливается необходимость изменения других объектов, работающих совместно с данным, оценивается возможность применения измененного объекта или найденной технической идеи при решении других задач.
На следующей стадии – постановки задачи – определяется конечная цель решения задачи, проверяется возможность достижения той же цели более простыми средствами, выбирается наиболее эффективный путь решения и определяются требуемые количественные показатели.
Аналитическая стадия включает определение конечного результата, который желательно получить в самом идеальном случае, также выявляются препятствия, мешающие достижению идеала, и их причины, определяются условия, обеспечивающие получение идеального результата с целью найти, при каких условиях исчезнет «помеха».
При проведении теоретических исследований широко используются методы расчленения и объединения элементов исследуемой системы (объекта, явления).
Метод расчленения предложен французским философом и естествоиспытателем Р. Декартом. В своей работе «Правила для руководства ума» он пишет: «Освободите вопрос от всех излишних представлений и сведите его к простейшим элементам». В процессе расчленения выделяются существенные и несущественные параметры, основные элементы и связи между ними. Следует, однако, отметить, что каждый объект можно расчленить разными способами, и это существенно влияет на проведение теоретических исследований, так как в зависимости от способа расчленения процесс изучения объекта может упроститься или, при неправильном расчленении, наоборот, усложниться. После расчленения объекта изучается вид взаимосвязи элементов и осуществляется моделирование каждого структурного элемента. На завершающей стадии исследования элементы объединяются в сложную модель объекта.
Упрощения, которые вводятся на всех этапах построения модели объекта, сопровождаются определенными допущениями, которые должны быть осознанными и обоснованными. Неверные допущения могут приводить к серьезным ошибкам при формулировании теоретических выводов.
Метод объединения, противоположный методу расчленения, тесно связан с комплексным подходом к изучению объекта. Их объединение называют «общей теорией систем», или «системологией».
Общая теория систем (ОТС) возникла на основе изучения некоторых биологических объектов и явлений и впервые была сформулирована Л. Берталанфи. Со временем в ее структуре выделились два направления. Цель первого – развитие ОТС как некоторой философской концепции, включающей в себя такие понятия, как принцип системности, системный подход, системный анализ и т. д. В другом направлении общая теория систем представляет собой некоторый математический аппарат, претендующий на строгое описание закономерностей формирования и развития любых систем.
ОТС базируется на трех постулатах, которые дают возможность определения организации системы, исходя из характеристик взаимодействия с внешней средой, а характеристик взаимодействия, в свою очередь, исходя из организации системы.
Первый постулат утверждает, что функционирование систем любой природы может быть описано на основе рассмотрения структурно-функциональных связей между отдельными элементами систем. Второй постулат состоит в том, что организация системы может быть установлена на основе проведенных извне системы наблюдений за элементами, которые непосредственно взаимодействуют с ее окружением. Третий постулат гласит, что организация системы полностью определяет ее функционирование и характер взаимодействия с окружающей средой.
При разработке теорий наряду с вышеизложенными методами используются логические методы и правила, носящие нормативный характер. К их числу относятся правила вывода сложных понятий из простых, установления истинности сложных высказываний. Для построения теорий применяют также принципы формирования аксиоматических теорий, критерии непротиворечивости, полноты и независимости систем аксиом и гипотез и др.
Теоретические исследования играют большую роль в процессе познания объективной действительности, поскольку они позволяют глубоко проникать в сущность природных явлений, создавать постоянно развивающуюся научную картину мира.
7.2 Выбор типа математической модели
В технических науках необходимо стремиться к применению математической формализации выдвинутых гипотез и выводов. При решении практических задач математическими методами осуществляются математическая формулировка задачи (разработка математической модели), выбор метода исследования полученной модели, анализ полученного математического результата.
Математическая модель представляет собой систему математических соотношений – формул, функций, уравнений, систем уравнений, описывающих те или иные стороны изучаемого объекта, явления, процесса. Для моделирования могут быть использованы непрерывные или дискретные, детерминированные или вероятностные функции.
Анализ информационного массива позволяет установить непрерывность или дискретность исследуемого показателя и объекта в целом. В непрерывных процессах все сигналы представляют собой непрерывные функции времени. В дискретных – все сигналы квантуются по времени и амплитуде. Если сигналы квантуются только по времени, то есть представляются в виде импульсов с равной амплитудой, то такие объекты называют дискретно-непрерывными. Установление непрерывности объекта позволяет использовать для его моделирования дифференциальные уравнения. Одним из методов исследования дискретных процессов является теория автоматов.
Первым этапом математического моделирования является постановка задачи, определение объекта и целей исследования. Весьма важным на этом этапе является установление границ области влияния изучаемого объекта. Границы области влияния объекта определяются областью значимого взаимодействия с внешними объектами. Данная область может быть определена так: границы области охватывают те элементы, воздействие которых на исследуемый объект существенно; за этими границами действие исследуемого объекта на внешние объекты стремится к нулю. Это позволяет рассматривать моделируемую систему как замкнутую (то есть, с известной степенью приближения, независимую от внешней среды), что упрощает математическое исследование.
Следующим этапом является выбор типа математической модели. Обычно строится несколько моделей, на основе сравнения результатов исследования которых с реальностью устанавливается наилучшая. Если оказывается, что для формирования математической модели недостаточно исходных данных, то выполняется поисковый эксперимент, в ходе которого устанавливаются: линейность или нелинейность, динамичность или статичность, стационарность или нестационарность, а также степень детерминированности исследуемого объекта или процесса.
Линейность устанавливается по характеру статической характеристики исследуемого объекта. Под статической характеристикой объекта понимается связь между величиной внешнего воздействия на объект (значением входного сигнала) и его реакцией на внешнее воздействие (значением выходного сигнала). Под выходной характеристикой системы понимается изменение выходного сигнала системы во времени. Если значения выходного и входного сигналов прямо пропорциональны, то моделирование объекта осуществляется с использованием линейных функций. Нелинейность статической характеристики и наличие запаздывания в реагировании объекта на внешнее воздействие являются яркими признаками нелинейности. В этом случае для моделирования объекта должна быть принята нелинейная математическая модель.
Установление динамичности или статичности осуществляется по поведению исследуемых показателей объекта во времени. Применительно к детерминированной системе можно говорить о статичности или динамичности по характеру ее выходной характеристики. Если среднее арифметическое значение выходного сигнала по разным отрезкам времени не выходит за допустимые пределы, определяемые точностью методики измерения исследуемого показателя, то это свидетельствует о статичности объекта. Весьма важным является выбор отрезков времени, на которых устанавливается статичность или динамичность объекта. Если объект на малых отрезках времени оказался статичным, то при увеличении этих отрезков результат не изменится. Если же статичность установлена для крупных отрезков времени, то при их уменьшении результат может измениться и статичность объекта может перейти в динамичность.
Объект исследования можно считать стационарным, если в ходе ряда экспериментов установлено, что значение фиксируемого параметра в течение всего времени наблюдения не выходит за пределы отклонения, соответствующего ошибке измерения.
Первоначальные данные об исследуемом объекте либо результаты поискового эксперимента позволяют установить схему взаимодействия объекта с внешней средой по соотношению входных и выходных величин. Возможны четыре схемы взаимодействия:
– одномерно-одномерная схема (рисунок 7.1, а) – на объект воздействует только один фактор, а его влияние оценивается по одному показателю (один выходной сигнал); связь выходного сигнала y с входным x может быть описана функцией y = f(x), в качестве которой чаще всего принимают полином;
– одномерно-многомерная схема (рисунок 7.1, б) – действие одного фактора оценивается несколькими показателями, при этом по аналогии с предыдущей схемой определяются отдельно математические модели входного воздействия с каждым выходным сигналом, которые считаются независимыми;
– многомерно-одномерная схема (рисунок 7.1, в) – на объект воздействует несколько факторов, а его поведение оценивается по одному показателю;
– многомерно-многомерная схема (рисунок 7.1, г) – на объект воздействует множество факторов и его поведение оценивается по множеству показателей, при этом математическая модель принимается аналогичной многомерно-одномерному взаимодействию, но учитываются как независимые действия на объект, так и особенности, появляющиеся в результате совместного воздействия факторов.
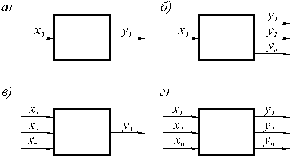
Рисунок 7.1 – Схемы моделей взаимодействия объекта с внешней средой
Если при использовании многомерно-одномерной и многомерно-многомерной схем для описания зависимости каждого выходного сигнала от входного применяется линейная математическая модель, то появляется возможность использования принципа суперпозиции. Он утверждает, что когда на линейную систему воздействуют несколько входных сигналов, то каждый из них фильтруется системой так, как будто никакие другие сигналы на нее не действуют. Общий выходной сигнал линейной системы образуется в результате суммирования ее реакции на каждый входной сигнал. В случае многомерно-одномерной схемы связь между выходным и входным сигналами описывается выражениями:
– при равнозначности внешних воздействий ![]() ;
;
– при неравнозначности внешних воздействий ![]() ,
,
где аn – постоянный коэффициент.
Процесс выбора математической модели объекта заканчивается ее предварительным контролем. При этом осуществляются следующие виды контроля:
– контроль размерностей сводится к проверке выполнения правила, согласно которому приравниваться и складываться могут только величины одинаковой размерности;
– контроль порядков направлен на упрощение модели, он предполагает определение порядков складываемых величин и отбрасывание малозначительных слагаемых;
– контроль характера зависимостей предполагает проверку направления и скорости изменения одних величин при изменении других; явления, вытекающие из математической модели, должны соответствовать физическому смыслу задачи;
– контроль экстремальных ситуаций заключается в проверке наглядного смысла решения при приближении параметров модели к особым точкам, например, к нулю или бесконечности;
– контроль граничных условий состоит в проверке правильности учета всех связей, наложенных на объекты математической модели, в том числе соответствия им граничных условий;
– контроль математической замкнутости сводится к проверке того, что математическая модель дает однозначное решение;
– контроль физического смысла предполагает анализ физического содержания промежуточных соотношений, используемых при построении математической модели;
– контроль устойчивости модели осуществляется путем варьирования исходных данных в рамках имеющейся информации о реальном объекте, причем оно не должно приводить к существенному изменению решения.
Цель и задачи, которые ставятся при математическом моделировании, играют немаловажную роль при выборе типа модели. Практические задачи требуют простого математического аппарата, а фундаментальные – более сложного, допускают прохождение иерархии математических моделей. В настоящее время при решении технических задач появляется необходимость в привлечении сложного математического аппарата, который сосредоточен в вычислительных программных комплексах инженерного анализа.
7.3 Особенности конечноэлементного моделирования
Конструкции транспортных средств состоят из большого количества деталей, большинство которых имеет сложную форму. Расчет напряженно-деформированного состояния таких деталей аналитическими методами весьма сложен либо вовсе невозможен, так как требует решения систем нелинейных дифференциальных уравнений в частных производных. Поэтому широкое распространение получили численные методы прочностных расчетов. Наиболее известен из них метод конечных элементов (МКЭ). Идея его заключается в том, что всю область решения разбивают на подобласти достаточно малых конечных размеров и в пределах каждой такой подобласти используют чаще всего линейную аппроксимацию для представления искомой функции, при этом решение задачи получается в результате объединения найденных кусочных решений.
Решение задач прочности с применением МКЭ во многом зависит от правильного выбора расчетной схемы, аппроксимирующих ее конечных элементов, законов распределения действующих нагрузок, мест их приложения, определения наиболее нагруженных зон.
Процесс создания конечноэлементной модели включает ряд процедур, представленных на рисунке 7.2.
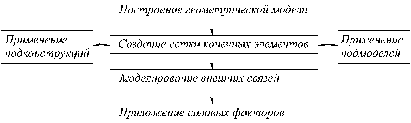
Рисунок 7.2 – Схема формирования конечноэлементной модели
Первая стадия – геометрическое моделирование – включает разработку пространственной модели конструкции с учетом всех тех ее параметров, которые могут оказать существенное влияние на результаты расчетов. На этой стадии помимо ввода геометрических размеров конструкции задаются свойства материалов, из которых она изготовлена. При создании геометрической модели могут импортироваться чертежи конструкции, выполненные в инженерных CAD программах.
На этапе создания сетки конечных элементов выясняется целесообразность использования различных видов конечных элементов (балочных, оболочечных, объемных и т. д.) в рассматриваемой модели. На этой стадии выполняются мероприятия по созданию максимально возможного количества областей с регулярной сеткой конечных элементов. В тех местах, где предполагается концентрация напряжений, необходимо использование более мелкой сетки. Для более детального рассмотрения некоторых областей, а также для снижения трудоемкости работы и времени расчета применяют методы подмоделей и подконструкций. На рисунке 7.3 представлена схема разбиения на конечные элементы модели железнодорожной цистерны при расчете конструкции на прочность.
На стадии моделирования внешних связей следует учитывать особенности взаимодействия деталей конструкции при различных вариантах нагружения. Количество связей и их виды должны быть такими, чтобы обеспечить построение кинематически неизменяемой модели.
Приложение силовых факторов должно соответствовать реальной работе конструкции при рассматриваемых режимах эксплуатации. На этой стадии устанавливаются законы распределения активных сил по объему или поверхности конструкции.
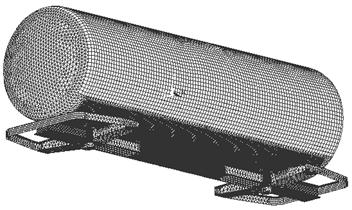
Рисунок 7.3 – Конечноэлементная модель железнодорожной цистерны
модели 15-1443
После создания конечноэлементной модели выполняется расчет конструкции, который включает три этапа:
– задание аппроксимирующей функции для каждого отдельного конечного элемента;
– объединение конечных элементов в ансамбль;
– нахождение значений функции в узлах модели, которые соответствуют заданным граничным условиям.
В настоящее время создано большое количество программных продуктов, реализующих описанный алгоритм, таких как ANSYS, ADAMS, NASTRAN, MARC и др.
Применение метода конечных элементов позволяет еще на стадии проектирования проработать различные конструктивные решения тех или иных узлов и выбрать из них наилучшие, до минимума сократив при этом затраты средств на дорогостоящие натурные испытания.
8 НАУЧНЫЕ ДОКУМЕНТЫ И ИЗДАНИЯ
8.1 Оформление результатов научной работы
Для того чтобы результаты научной деятельности могли быть использованы на практике, важно не только грамотно организовать и провести изучение объекта, но и правильно оформить результаты научных изысканий. Объектом, содержащим научно-техническую информацию и предназначенным для ее хранения и использования, является научный документ. Он может представлять собой отчет, доклад, статью и т. д.
При подготовке научной рукописи наряду с ясностью изложения, системностью и последовательностью в подаче материала необходимо соблюдать определенные требования к оформлению.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |



