Методы теоретического уровня предназначены для логического исследования собранных фактов, выработки понятий, суждений, формирования умозаключений. На этом уровне научное мышление освобождается от эмпирической описательности, создает теоретические обобщения. Устанавливается соответствие ранних научных представлений с возникающими новыми, и новые теоретические знания надстраиваются над эмпирическими. Здесь широко используются логические методы сходства, различия, сопутствующих изменений. К методам теоретического уровня относятся: абстрагирование, идеализация, формализация, анализ и синтез, индукция и дедукция, аксиоматика, обобщение и др.

Абстрагирование – это мысленное отвлечение от несущественных свойств, связей, отношений предметов и выделение нескольких сторон, интересующих исследователя. Оно, как правило, осуществляется в два этапа. На первом этапе определяются несущественные свойства, связи и т. д. На втором – исследуемый объект заменяют другим, более простым, представляющим собой упрощенную модель, сохраняющую главное в сложном.

Идеализация – это мысленное конструирование объектов, которые практически неосуществимы (например, идеальный газ, абсолютно твердое тело). Она применяется при гипотетическом методе познания. В результате идеализации реальные объекты могут быть лишены некоторых присущих им свойств и наделены свойствами, соответствующими рабочей гипотезе.

Формализация – отображение объекта или явления в знаковой форме какого-либо символьного языка (математики, химии и т. д.) и обеспечение возможности исследования реальных объектов и их свойств через формальное исследование соответствующих знаков.

Аксиоматический метод – способ построения научной теории, при котором некоторые утверждения (аксиомы) принимаются без доказательства и затем используются для получения остальных знаний по определенным логическим правилам.

Обобщение – определение общего понятия, в котором находит отражение главное, характеризующее объекты данного класса. Это средство для образования новых научных понятий, формулирования законов и теорий.

Методы метатеоретического уровня предназначены для исследования самих теорий и разработки путей их построения. С их помощью изучается система положений и понятий данной теории, устанавливаются границы ее применения, способы введения новых понятий, обосновываются пути синтезирования нескольких теорий. К методам рассматриваемого уровня относят диалектический метод и метод системного анализа.

Диалектический метод разрабатывает подходы к развитию теорий на основе применения общефилософских положений к решению частных задач.

Системные методы используются при исследованиях сложных систем с многообразными связями, характеризуемыми непрерывностью и дискретностью, детерминированностью и случайностью. К числу таких методов относятся исследование операций, теория массового обслуживания, теория управления, теория множеств и др. В настоящее время такие методы получили широкое распространение в связи с развитием ЭВМ.

При анализе явлений и процессов в сложных системах возникает потребность рассматривать большое количество факторов (признаков), среди которых важно уметь выделять главные и исключать второстепенные, существенно не влияющие на исследуемое явление. Для этого используется метод ранжирования. Он допускает усиление основных и ослабление второстепенных факторов, то есть размещение их по определенным правилам в ряд убывающей или возрастающей последовательности по силе фактора.

5.2 Основные понятия моделирования

Моделированием называется замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели. Моделирование применяется обычно в тех случаях, когда исследование непосредственно на натурном объекте затруднительно либо опасно.

Модель (в переводе с французского – образец) – это упрощенная форма представления реальных процессов и взаимосвязей в системе, позволяющая изучить, оценить и прогнозировать влияние составляющих элементов (либо отдельных факторов) на поведение системы в целом. В научном исследовании под моделью понимают искусственно созданную систему, которая в определенном отношении схожа с исследуемым объектом, так как воспроизводит его характерные черты и явления, происходящие в натурных условиях.

Все многообразие моделей можно разделить на 2 класса: вещественные (физические или для объектов техники механические) и воображаемые (математические).

Физической моделью может считаться установка, в которой осуществлено полное или неполное моделирование и соответственно физическое подобие, благодаря чему по характеристикам модели можно получать все существенные для данной задачи характеристики натурного объекта умножением на масштабные коэффициенты. Физическая модель отличается от натурного объекта своими размерами, но процессы, совершающиеся в ней, по своей природе не отличаются от процессов, происходящих в натуре (то есть это копия физически реальной системы), например, модели самолетов и их испытания в аэродинамических трубах. Физическое моделирование целесообразно в тех случаях, когда исследовать влияние изменения конструктивных параметров на те или другие процессы на натурном объекте очень трудоемко и дорого либо вовсе невозможно.

Другим видом вещественного моделирования является моделирование по аналогии, при котором модель и натурный объект или явление имеют различную физическую природу, но описываются однотипными уравнениями. Моделирование по аналогии гораздо проще и дешевле физического, так как оно может осуществляться на ЭВМ или с помощью электрических или иных моделей. Однако для исследуемого процесса не всегда удается получить необходимое аналитическое выражение, а без этого моделирование по аналогии невозможно.

В качестве примера моделирования по аналогии рассмотрим колебания вагона на рессорах. Упрощенная схема механической системы вагона представляет собой тело массы m, установленное на пружину с коэффициентом жесткости Cп, как это показано на рисунке 5.1, а. Свободные колебания такой системы описываются уравнением

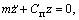(5.1)

где – вертикальная координата центра масс вагона.

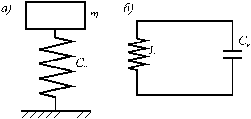
Рисунок 5.1 – Механическая модель и электрический аналог

Уравнения электрических колебаний в контуре, включающем конденсатор с электрической емкостью Cк и катушку индуктивностью L, схема которого представлена на рисунке 5.1, б, описываются уравнением

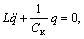(5.2)

где q – заряд на одной из обкладок конденсатора.

Если в уравнениях (5.1) и (5.2) сделать подстановки

,

то оба уравнения примут одинаковую форму

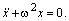
Следовательно, существует аналогия электрической и механической систем, причем w имеет смысл круговой частоты собственных колебаний, масса механической системы m соответствует индуктивности L, а коэффициент жесткости пружины Cп соответствует величине, обратной электрической емкости Cк.

Под математическим моделированием понимается процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики исследуемого натурного объекта или процесса. Математическая модель представляет собой систему математических соотношений – формул, функций, уравнений, описывающих те или иные стороны изучаемого объекта, явления, процесса. При этом подобие физических процессов модели и оригинала не сохраняется. Вид математической модели зависит как от природы реального объекта, так и от задач исследования и требуемой точности решения. Математическое моделирование, методика которого рассмотрена в разделе 7, относится к воображаемому, логическому моделированию.

В настоящее время широко используются такие виды математического моделирования, как структурное, цифровое, функциональное.

Первым этапом структурного моделирования является создание математических моделей отдельных частей исследуемого объекта или процесса. В результате их объединения в единую систему и расположения в определенной последовательности с учетом взаимодействий между частями получается математическая модель структурного типа.

При цифровом моделировании элементы, производящие математические операции, являются дискретными. На современном этапе развития техники и информационных технологий такое моделирование выполняется с помощью ЭВМ, поэтому его также называют компьютерным моделированием. Преимуществом цифровых моделей является возможность получения результатов с высокой точностью.

Функциональное моделирование – это моделирование, осуществляемое на установках, в которых комплекс моделируемых явлений не только не сохраняет физическую природу, но может и не описываться формально одинаковыми уравнениями. При функциональном моделировании подобными считаются явления, которые в каком-то смысле, в отношении каких-то частных процессов или отдельных их сторон дают похожие результаты.

5.3 Условия механического подобия

При создании моделей следует стремиться к идентичности характеристик модели и натурного объекта. Чтобы достичь такого соответствия, разработана специальная теория механического подобия.

Низшей ступенью подобия является геометрическое подобие. Подобными в геометрии называются фигуры, имеющие одинаковые формы и пропорциональные размеры. Отношение длин линий фигур называется масштабом, или коэффициентом подобия.

Механическое подобие – более высокая ступень подобия. В механической модели соблюдение геометрического подобия обязательно. Однако необходимо еще и подобие физических параметров модели и натурного объекта, которое должно распространяться только на те характеристики, которые имеют существенное значение для изучаемого явления. Например, если внутренние напряжения в материале котла цистерны не влияют на исследуемый процесс колебаний жидкости в ней, то модель может быть изготовлена из любого материала, в том числе прозрачного, так как в этом случае подобие характеристик материала необязательно. Подобия геометрических и физических параметров являются условиями однозначности модели и натурного объекта.

Для перехода от характеристик натурного объекта к характеристикам модели используется понятие коэффициента подобия. Такие коэффициенты для данной модели являются постоянными величинами.

Для пояснения принципа определения коэффициентов подобия рассмотрим ситуацию, в которой необходимо исследовать динамику объекта на модели, размеры которой в kl раз меньше, чем размеры натурного объекта. В этом случае kl называют коэффициентом подобия линейных размеров. Если модель изготовлена из материала, плотность r которого в kr раз меньше плотности оригинала, то масса модели может быть рассчитана по формуле

.

Поскольку объем модели в (kl)3 раз меньше объема натурного объекта, то их масса будет различаться в kr (kl)3 раз. Полученное произведение является коэффициентом подобия масс km. Движение такого объекта описывается основным законом динамики Ньютона , где a – ускорение, которое определяется двукратным дифференцированием линейных размеров

.

Следовательно, чтобы вычислить коэффициент подобия для ускорений модели и натурного объекта, нужно коэффициент подобия длины разделить на квадрат коэффициента подобия времени (знаки дифференцирования d не влияют на размерность):

.

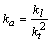Аналогично рассуждая, получаем, что коэффициент подобия для сил

.

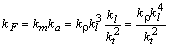Таким образом, чтобы движение модели полностью соответствовало движению натурного объекта, необходимо отличие приложенных к нему сил в kF раз.

Иногда бывает полезно установить, при каком соотношении между параметрами модели и натурного объекта явления, происходящие в них, будут физически подобны. Это устанавливается с помощью критериев подобия. Чтобы получить один из таких критериев, снова рассмотрим движение объекта и его модели под действием приложенных к ним сил.

Для обоих тел основной закон динамики запишется в виде:

или

Разделив обе части уравнения на Fi, получаем

.

Следовательно, подставляя в предыдущее равенство вместо физических величин соответствующие коэффициенты подобия, получаем

,

что соответствует условию

Последнее соотношение устанавливает соответствие между параметрами исследуемого объекта и модели, и его называют критерием подобия (этот критерий установлен еще Ньютоном, поэтому носит его имя).

Для многих физических явлений установление критериев не только полезно, но и исключительно важно, так как описание этих явлений производится с помощью критериев подобия или в критериальной форме. Приведем некоторые наиболее распространенные критерии механического, гидродинамического, электрического и теплового подобия.

1 Объект движется ускоренно в поле тяготения. В этом случае используется критерий подобия Фруда Fr:

,

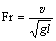где – скорость объекта;

g – ускорение свободного падения.

2 Если на движущиеся объект исследования и его модель действуют помимо прочих сил силы упругости, подчиняющиеся закону Гука, то применяют критерий подобия Коши C:

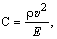
где r – плотность;

E – модуль упругости.

3 Объект движется с ускорением в вязкой несжимаемой жидкости. В данном случае моделирования помимо общего критерия подобия Ньютона следует принимать в качестве определяющего критерий Рейнольдса Re:

,

где d – гидравлический диаметр;

ν – кинематическая вязкость жидкости.

Все подобия подчиняются некоторым общим закономерностям, которые устанавливаются теоремами подобия [12]. Основное предназначение этих теорем – обоснование возможности записи уравнений, описывающих сложные нелинейные системы, в безразмерной форме. Такая форма позволяет выяснить общие закономерности поведения рассматриваемых систем и установить влияние разных факторов на параметры исследуемых процессов.

Существенная особенность критериев подобия – их безразмерность. Физические характеристики, входящие в выражение любого критерия, таковы, что все размерности сокращаются, поэтому величина критерия – число отвлеченное и, таким образом, сохраняющее одно и то же значение в любой системе единиц.

Критерии подобия процесса могут быть найдены, если известно его математическое описание или хотя бы та совокупность параметров, которой в данной задаче и в данных условиях можно характеризовать изучаемое явление. Однако история дает немало примеров, когда создатели моделей не знали критериев подобия и не пользовались ими. Так обстояло дело на заре моделирования в технике. Подобная ситуация, в частности, наблюдается в тех областях науки (например, в биологии и медицине), где по тем или иным причинам математика еще в достаточной мере не пришла на помощь ученым и количественные оценки явлений только еще начинают проникать в методологию таких исследований.

6 ОСОБЕННОСТИ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ

6.1 Типы и задачи экспериментальных исследований,

их классификация

Важнейшей составной частью научных исследований является эксперимент, основой которого является научно поставленный опыт с точно учитываемыми и управляемыми условиями. Само слово эксперимент происходит от лат. experimentum – проба, опыт. В научном языке и исследовательской работе термин «эксперимент» обычно используется в значении, общем для целого ряда сопряженных понятий: опыт, целенаправленное наблюдение, воспроизведение объекта познания, организация особых условий его существования, проверка предсказания. В это понятие вкладывается научная постановка опытов и наблюдение исследуемого явления в точно учитываемых условиях, позволяющих следить за ходом явления и воссоздавать его каждый раз при повторении этих условий. Само по себе понятие «эксперимент» означает действие, направленное на создание условий для осуществления того или иного явления по возможности наиболее частого, т. е. не осложняемого другими явлениями. Основными целями эксперимента являются выявление свойств исследуемых объектов, проверка справедливости гипотез и на этой основе широкое и глубокое изучение темы научного исследования. Постановка и организация эксперимента определяются его назначением.

Структура эксперимента включает: построение модели объекта исследования, сознательное и планомерное изменение, комбинирование условий эксперимента и воздействий на объект, получение экспериментальных данных, их обработку. На всех стадиях исследования должно контролироваться соблюдение объективных законов науки. По результатам эксперимента формируются выводы.

Экспериментальные исследования, которые проводятся в различных отраслях науки, классифицируют по ряду признаков.

По способу формирования условий выделяют естественный и искусственный эксперименты.

Естественный предполагает проведение опытов в естественных условиях существования объекта исследования (чаще всего используется в биологических, социальных, педагогических и психологических науках).

При искусственном эксперименте формируются искусственные условия (широко применяется в естественных и технических науках).

По целям исследования различают эксперименты преобразующие, констатирующие, контролирующие, поисковые и решающие.

Преобразующий (созидательный) эксперимент включает активное изменение структуры и функций объекта исследования в соответствии с выдвинутой гипотезой, формирование новых связей и отношений между компонентами объекта или между исследуемым объектом и окружающей средой. В нем преднамеренно создают условия, которые должны способствовать формированию новых свойств и качеств объекта.

Констатирующий эксперимент используется для проверки определенных предположений. В его процессе констатируется наличие определенной связи между воздействием на объект исследования и результатом, выявляется наличие определенных фактов.

Контролирующий эксперимент сводится к контролю за результатами внешних воздействий на объект исследования с учетом его состояния, характера воздействия и ожидаемого эффекта.

Поисковый эксперимент проводится в том случае, если затруднена классификация факторов, влияющих на изучаемое явление вследствие отсутствия достаточных предварительных данных. По его результатам устанавливается значимость параметров, осуществляется отсеивание малозначимых.

Решающий эксперимент ставится для проверки справедливости основных положений фундаментальных теорий в том случае, когда две или несколько гипотез одинаково согласуются со многими явлениями. Его цель – выявление наиболее справедливой гипотезы.

По организации проведения бывают эксперименты лабораторные и натурные.

Лабораторный эксперимент проводится в лабораторных условиях с применением типовых приборов, специальных моделирующих установок, стендов, оборудования и т. д., и изучается не сам объект, а его образец. Этот эксперимент позволяет изучить влияние одних характеристик при варьировании других, получить научную информацию с минимальными затратами времени и ресурсов. Однако такой эксперимент не всегда полностью моделирует реальный ход изучаемого процесса, поэтому возникает потребность в проведении натурного эксперимента.

Натурный эксперимент проводится в естественных условиях и на реальных объектах. Он часто используется в процессе испытаний изготовленных систем. В зависимости от места проведения испытаний натурные эксперименты подразделяются на производственные, полевые, полигонные, полунатурные и т. п. Натурный эксперимент всегда требует тщательного продумывания и планирования, рационального подбора методов исследования. Практически во всех случаях основная научная проблема натурного эксперимента – обеспечить адекватность условий эксперимента реальной обстановке, в которой будет работать создаваемый объект. Основными задачами натурного эксперимента являются изучение характеристик воздействия среды на испытуемый объект, идентификация статистических и динамических параметров объекта, оценка эффективности функционирования объекта и проверка его на соответствие заданным требованиям.

По структуре изучаемых объектов и явлений различают простой и сложный эксперименты.

Простой используется для изучения объектов с небольшим количеством взаимосвязанных и взаимодействующих элементов, выполняющих простейшие функции и не имеющих разветвленной структуры.

В сложном эксперименте изучаются явления или объекты с большим количеством взаимосвязанных и взаимодействующих элементов и выполняющих сложные функции. Они имеют разветвленную структуру, в которой можно выделить иерархические уровни. Высокая степень связности элементов приводит к тому, что изменение состояния какого-либо элемента или связи влечет за собой изменение состояния многих других элементов системы.

По характеру внешних воздействий на объект исследования выделяют вещественный, энергетический и информационный эксперименты.

Вещественный – рассматривает влияние воздействия физических тел на состояние объекта исследования.

Энергетический эксперимент применяется для изучения влияния на объект исследования различных видов энергии (электромагнитной, тепловой, механической и т. д.). Этот тип эксперимента широко распространен в естественных науках.

Информационный эксперимент используется для изучения воздействия определенной информации на объект исследования. Он чаще всего применяется в биологии, психологии, кибернетике и т. п.

По характеру взаимодействия средства экспериментального исследования с объектом исследования существуют обычный и модельный эксперименты.

Обычный (или классический) эксперимент включает экспериментатора как познающего субъекта, а также объект или предмет экспериментального исследования и средства его осуществления (инструменты, приборы, экспериментальные установки). Причем экспериментальные средства непосредственно взаимодействуют с объектом исследования.

Модельный эксперимент в отличие от обычного имеет дело с моделью исследуемого объекта. Модель входит в состав экспериментальной установки, замещая не только объект исследования, но часто и условия, в которых изучается некоторый объект. Различие между моделью и реальным объектом может стать источником ошибок, что требует дополнительных затрат времени и теоретического обоснования свойств модели.

По типу моделей, исследуемых в эксперименте, выделяют материальный и мысленный эксперименты.

В материальном эксперименте используются материальные объекты исследования.

Орудиями мысленного (умственного) эксперимента являются мысленные модели исследуемых объектов или явлений (чувственные образы, образно-знаковые модели, знаковые модели). Его называют также идеализированным или воображаемым экспериментом. Мысленный эксперимент является одной из форм умственной деятельности, в процессе которой воспроизводится в воображении структура реального эксперимента. Сходство мысленного эксперимента с реальным в значительной мере определяется тем, что всякий реальный эксперимент, прежде чем быть осуществлённым на практике, сначала проводится человеком мысленно (путем обдумывания и планирования). Поэтому мысленный эксперимент нередко выступает в роли идеального плана реального эксперимента, предваряя его. В то же время мысленный эксперимент может быть выполнен и в тех случаях, когда проведение реальных опытов оказывается невозможным.

По контролируемым величинам эксперименты разделяют на пассивный и активный.

Пассивный эксперимент предусматривает изменение только выбранных показателей (параметров, переменных) в результате наблюдения за объектом без искусственного вмешательства в его функционирование. Примером пассивного эксперимента в решении задач транспорта является подконтрольная эксплуатация транспортных средств. В этом случае выделяется специальная группа подконтрольных транспортных средств, в ходе которой фиксируется и накапливается информация о всех отказах и неисправностях, на каком пробеге они произошли или выявлены, данные о нагрузках, роде перевозимого груза и т. п. Пассивный эксперимент, по существу, является наблюдением, которое сопровождается либо инструментальным измерением, либо фиксированием выбранных показателей состояния объекта исследования. К достоинствам пассивного эксперимента относится его достоверность. Основной недостаток – информация слишком "запаздывает", т. е. время обратной связи весьма велико. Например, от разработки какого-либо узла до момента поступления информации о его надежности из сферы эксплуатации проходит несколько лет. Устранить данный недостаток, получить оперативную информацию о надежности позволяют: обработка результатов незавершенных испытаний с использованием специальных математических методов, применение методов статистического моделирования на основании предварительных результатов пассивного эксперимента, а также проведение специальных активных экспериментов.

Активный эксперимент связан с выбором входных сигналов (факторов) и контролирует вход и выход исследуемой системы. В этом случае исследователь организует и активно влияет на ход эксперимента, задавая различные нагрузки, изменяя продолжительность их воздействия, изменяет количество и виды входных параметров и их вариацию. В настоящее время активные эксперименты проводят по специальным планам (программам), которые разрабатывают перед их проведением. План активного эксперимента включает: цель и задачи эксперимента; выбор варьируемых факторов; обоснование объема эксперимента, числа опытов; порядок реализации опытов, определение последовательности изменения факторов, задание интервалов между будущими экспериментальными точками; обоснование средств измерений; описание проведения эксперимента; обоснование способов обработки и анализа результатов эксперимента. Решение названных вопросов производится на основании специальной математической теории планирования эксперимента, что позволяет оптимизировать объем исследований и повысить их точность.

По числу варьируемых факторов существуют однофакторный и многофакторный эксперименты.

Однофакторный эксперимент предполагает исключение малозначимых факторов, выделение существенных факторов и их поочередное варьирование.

Суть многофакторного эксперимента состоит в том, что варьируются все переменные одновременно, и влияние каждой оценивается по результатам всех опытов, проведенных в данной серии экспериментов.

Конечно, для классификации могут быть использованы и другие признаки. Приведенная классификация экспериментальных исследований не может быть признана полной, поскольку с расширением научного знания расширяется и область применения экспериментального метода. Кроме того, в зависимости от задач эксперимента различные его типы могут объединяться, образуя комплексный, или комбинированный, эксперимент.

6.2 Вычислительный эксперимент

В последнее время в связи с быстрым развитием компьютерных технологий большое значение приобрел вычислительный эксперимент – исследование, основанное на применении прикладной математики и ЭВМ как технической базы при использовании математических моделей.

Вычислительный эксперимент основывается на создании математических моделей изучаемых объектов, которые формируются с помощью некоторой особой математической структуры, способной отражать свойства объекта, проявляемые им в различных экспериментальных условиях. Однако эти математические структуры превращаются в модели лишь тогда, когда элементы структуры имеют конкретную физическую интерпретацию. Получаемые математические структуры вместе с описанием соответствия экспериментально обнаруженным свойствам объекта и являются моделью изучаемого объекта. Они отражают в математической, символической (знаковой) форме объективно существующие в природе зависимости, связи и законы. Модель может соответствовать наглядным образом реальному устройству или какому-либо его элементу.

Вычислительный эксперимент основывается как на математической модели, так и на приемах вычислительной математики, которая состоит из многих разделов, развивающихся вместе с развитием вычислительной техники. Так, например, относительно недавно появился дискретный анализ, дающий возможность получения любого численного результата только с помощью арифметических и логических действий. Задача вычислительной математики здесь сводится к представлению решений (точно или приближенно) в виде последовательности арифметических операций, то есть алгоритма решения.

На основе математического моделирования и методов вычислительной математики разработаны теория и практика вычислительного эксперимента, технологический цикл которого принято разделять на ряд этапов.

1 Для исследуемого объекта строится модель, обычно сначала физическая, фиксирующая разделение всех действующих в рассматриваемом явлении факторов на главные и второстепенные, причем второстепенные факторы, которые не имеют существенного значения для рассматриваемого вопроса, на данном этапе исследования отбрасываются. Формулируются допущения и условия применимости модели, границы, в которых будут справедливы полученные результаты. Модель записывается в виде математических соотношений, как правило, в виде дифференциальных уравнений.

2 Разрабатывается метод решения сформулированной математической задачи, на основе которого в дальнейшем строится алгоритм. Каждый конкретный расчет в вычислительном эксперименте проводится при фиксированных значениях всех параметров. При оптимизации конструкции устройства приходится проводить большое число расчетов однотипных вариантов задачи, отличающихся значениями некоторых исходных данных. Это предопределяет эффективность применения вычислительной техники.

3 Разрабатывается программа решения задачи на ЭВМ. В настоящее время исследователи, как правило, программируют не самостоятельно, а используют готовые универсальные инженерные программные комплексы, в которых уже реализованы типовые алгоритмы решения прикладных задач.

4 Проведение расчетов на ЭВМ. Результат получается в виде некоторой цифровой информации, которую далее необходимо будет проанализировать. Точность решения определяется при вычислительном эксперименте достоверностью модели, положенной в основу эксперимента, правильностью алгоритмов и программ (проводятся предварительные «тестовые» испытания).

5 Обработка результатов расчетов, их анализ и выводы. На этом этапе могут возникнуть как необходимость уточнения математической модели (усложнения или, наоборот, упрощения), так и предложения по созданию упрощенных инженерных способов решения и формул, дающих возможности получить необходимую информацию более простым способом.

Вычислительный эксперимент приобретает исключительное значение в тех случаях, когда натурные эксперименты и построение физической модели оказываются невозможными. Особенно ярко можно проиллюстрировать значение вычислительного эксперимента при исследовании масштабов современного воздействия человека на природу. То, что принято называть климатом – устойчивое среднее распределение температуры, осадков, облач­ности и т. д., – представляет собой результат сложного взаимодействия физических процессов, протекающих в атмосфере, на поверхности земли и в океане. Характер и интенсивность этих процессов в настоящее время изменяются значительно быстрее, чем в сравнительно близком геологическом прошлом в связи с воздействием загрязнения окружающей среды. Климатическую систему можно исследовать, строя соответствующую математическую модель, которая должна в развитии рассматривать взаимодействие между собой атмосферы, океана и суши. Физические эксперименты над климатической системой не только чрезвычайно дороги, но и весьма опасны, так как могут вывести ее из равновесия. Однако глобальный климатический эксперимент возможен, но не натурный, а вычислительный, проводящий исследования не реальной климатической системы, а ее математической модели.

В науке и технике известно немало областей, в которых вычислительный эксперимент оказывается единственно возможным при исследовании сложных систем. Кроме того, часто он экономически более выгоден, чем натурный эксперимент.

6.3 Методика проведения экспериментальных работ

Для проведения эксперимента любого типа необходимо провести ряд предварительных действий: разработать гипотезу, подлежащую проверке, создать программу экспериментальных работ, определить способы и приемы вмешательства в объект исследования, обеспечить условия для осуществления процедуры экспериментальных работ, разработать пути и приемы фиксирования хода и результатов эксперимента, подготовить средства эксперимента (приборы, установки, модели и т. п.), обеспечить эксперимент необходимым обслуживающим персоналом.

Особое значение имеет правильная разработка методики эксперимента. Методика – это совокупность мыслительных и физических операций, размещенных в определенной последовательности, в соответствии с которой достигается цель исследования. Она должна включать следующие составные элементы:

– проведение предварительного целенаправленного наблюдения над изучаемым объектом или явлением с целью определения исходных данных (гипотез, выбора варьируемых факторов);

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6