РАЗДЕЛ III. ТЕОРИЯ МИКРОЭКОНОМИКИ

Глава 8. Факторы производства и производственная функция

1. Теория факторов производства. Основные факторы производства и их классификация

Производство – это важнейшая сфера деятельности, в которой в результате использования производственных факторов создаются продукты и услуги для потребления. В экономической теории существуют различные подходы к выделению факторов производства и их классификации в отдельные группы.

Марксистская теория в качестве факторов производства выделяет рабочую силу, предметы и средства труда, подразделяя их на две большие группы: личный и вещественный факторы производства. Эти факторы образуют сложную взаимодействующую систему, эффективность которой определяется технологией и организацией производства. Технология предполагает использование разнообразных методов обработки, изменения свойств, формы, состояния предмета труда. Организация производства обеспечивает согласованное функционирование всех факторов производства, их количественное соотношение, взаимодополняемость и взаимозаменяемость.

Маржиналистская или неоклассическая теория традиционно выделяет четыре группы факторов производства: земля, труд, капитал, предпринимательская деятельность.

К фактору земля отнесены: природные богатства, леса, пахотные земли, залежи ископаемых и т. д.

Труд представлен интеллектуальной и физической деятельностью, направленной на изготовление благ и оказание услуг. Совокупность способностей, обусловленных здоровьем, образованием, профессиональным обучением представляет собой человеческий капитал. Чем квалифицированнее труд человека, тем выше его капитал, и, соответственно, доход по этому капиталу.

Капитал может выступать в денежной и вещественной форме. В денежной – это средства, используемые для приобретения необходимых компонентов производственного процесса. В вещественной форме – это совокупность благ, используемых в производстве товаров и услуг: инструменты, машины, оборудование, здания и т. д. Их техническое состояние непрерывно совершенствуется, что сказывается на общей результативности производственного процесса.

Предпринимательская деятельность – специфический фактор производства, впервые выделенный в 70-х гг. XIX в. А. Маршаллом как «организация» и впоследствии названный Й. Шумпетером «предпринимательство». Это деятельность по принятию организационных и управленческих решений, предполагающая инициативу, риск, новаторство.

Различия в классификации факторов обусловлены разным подходом к анализу производства. Если маржинализм рассматривает факторы как общие технико-экономические элементы, без которых невозможен процесс производства, то марксизм – как экономическую категорию, определяющую социальную направленность производства.

Данная классификация факторов производства не является исчерпывающей. Так, экономическая теория постиндустриального общества выделяет в качестве самостоятельных факторов информационный, экономический и экологический. Американский экономист Э. Денисон, изучая влияние факторов производства на темпы экономического роста, выделил на макроуровне 23 фактора, в том числе жилые здания, складские помещения, относящиеся к капиталу, полицейских и военнослужащих, включаемых в состав фактора «труд», и т. п.

2. Производственная функция. Свойства производственной функции

Для организации любого производственного процесса необходимы факторы производства.

Будем считать, что выпуск продукции произведен при использовании только двух факторов производства – труда и капитала . В общем виде производственная функция (1) имеет вид:

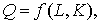
где – форма производственной функции. Производственная функция описывает технологическую взаимосвязь между объемом выпускаемой продукции и произведенными затратами факторов производства, а также зависимость между затратами. В функции находит отражение максимальный объем продукции, который достигается при каждой комбинации факторов, т. е. в определении производственной функции максимизация продукции решена технически. Если в качестве независимых переменных выступают величины затрат, то производственную функцию называют функцией выпуска, если же фиксирована величина выпуска, то производственная функция является функцией затрат.

При любой комбинации факторов можно достичь нескольких объемов выпуска в зависимости от эффективности организации производства. Если технология становится более прогрессивной, то производитель может увеличивать объем производства при фиксированном наборе производственных факторов. Производственная функция предполагает, что каждое сочетание факторов используется с максимальной эффективностью. Если используются n факторов производства, то производственная функция в общей форме имеет вид:

где – использованные факторы производства.

Если фиксирована величина выпуска, то производственная функция является функцией затрат и тогда затраты любого фактора можно выразить как функцию всех остальных затрат:

=,

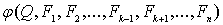где – форма функции.

Для укрупненного анализа и прогнозирования используется производственная функция Кобба-Дугласа*:

,

где – максимальный объем продукта при заданных факторах производства;

, – затраты труда, капитала;

– эффективность применяемой технологии.

, – коэффициенты эластичности объема производства, соответственно, по труду и капиталу или коэффициенты прироста , приходящиеся на 1% прироста соответствующего фактора. Названные коэффициенты в сумме измеряют совокупное процентное изменение выпуска при данном процентном изменении затрат труда и капитала. Если + =, то объём выпуска возрастает ровно на столько, на сколько увеличиваются затраты труда, капитала и материалов, имеет место постоянная отдача от масштаба, и функция Кобба-Дугласа в таком случае является однородной. Если 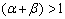, то предприятием будет получена экономия от масштаба, свидетельствующая о том, что эффективность факторов производства повышается в условиях технического прогресса. Если , будет иметь место убывающая отдача от масштаба производства.

Производственная функция обладает следующими свойствами.

1. Факторы производства являются взаимодополняющими. Для производства любого продукта используется определенный набор факто­ров, и отсутствие хотя бы одного из них делает производство невоз­можным. Это значит, что производственная функция превращается в нуль, когда один из факторов равен нулю: .

Кроме того, существует взаимозаменяемость факторов в определенной пропорции, которая обусловлена не только спецификой потребностей и конструктивными особенностями изделия, но и ограниченностью ресурсов, с одной стороны, и эффективностью их использования, с другой. Взаимозаменяемость не означает возможности полного исключения из производственного процесса какого-либо фактора, так как в любом случае необходима земля, на которой будет организован процесс производства, оборудование и труд работников.

2. Аддитивность отражает тот факт, что объединение двух групп факторов и дает, по крайней ме­ре, такой же объем продукции, как и при раздельном использовании этих двух групп факторов:

.

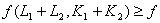
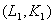
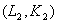3. Делимость означает, что любой производст­венный процесс может осуществляться в сокращенных масштабах. Например, при уменьшении числа рабочих и объема капитала вдвое выпуск продукции сократится не более, чем наполовину:

Данное положение не применимо на малых предприятиях, где производственная деятельность при уменьшающихся масштабах либо невоз­можна, либо неэффективна. Но такое свойство характерно для про­изводственной функции на уровне отрасли или народного хозяйства. Так, если в отрасли уменьшатся и занятость, и объем капитала на 10%, то это может означать остановку части предприятий при не­изменности условий работы на всех остальных.

Для исследования влияния факторов на объем выпуска используются понятия краткосрочного и долгосрочного периодов, а все факторы производства делятся на переменные и постоянные. Краткосрочный период – отрезок времени, в течение которого хотя бы один фактор остается неизменным. Долгосрочный период – отрезок времени, в течение которого могут быть изменены все факторы производства. Переменные факторы – это ресурсы, количества которых могут быть изменены в рамках краткосрочного периода. Постоянные – это ресурсы, количества которых не могут быть изменены в рамках краткосрочного периода.

Следует подчеркнуть, что хотя определения краткосрочного и долгосрочного периодов связаны со временем, их экономическое содержание обусловлено не временем, а реальными изменениями структуры производства. Поэтому, в силу технологических особенностей разных производств, временные рамки краткосрочного или долгосрочного периодов для каждого из них могут значительно различаться.

3. Изокванты

За редким исключением, конкретный продукт может быть произведен при использовании различных факторов производства в изменяющихся пропорциях. Оставим пока в стороне случаи, когда продукт можно произвести, используя факторы производства только в одной пропорции, и когда никакое замещение одного фактора другим невозможно. Другой крайний случай представляется ситуацией, когда используется бесконечное множество эффективных комбинаций факторов. Тогда можно изменять на бесконечно малую величину затраты одного фактора и увеличивать на бесконечно малую величину затраты другого фактора для производства заданного объема продукции. Такая производственная функция является непрерывной. В последующем это свойство функции будем часто использовать. Между названными крайними случаями находятся промежуточные, реалистические, когда данное количество продукции можно произвести с помощью определенного числа комбинаций факторов.

Допустим, что в производстве продукта используются только два фактора – труд L и капитал К. Максимальный выпуск Q можно получить при сочетаниях факторов: где п — любое положительное число. Построим кривую (рис. 8.1), каждой точке которой соответствует одно из сочетаний факторов. Это изокванта. На ней расположены все сочетания факторов производства, использование которых позволяет получить один и тот же объем продукции Q. Изокванта показывает, что объем продукции Q можно произвести при небольших затратах труда и больших затратах капитала , при небольших затратах капитала и больших затратах труда и т. д. Таким образом, производственная функция графически представляется изоквантой.

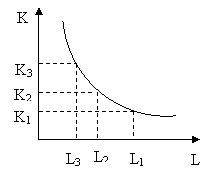Рис. 8.1. Изокванта.

Производственную функцию для различных объемов производства 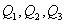представляют семейством изоквант (рис.8.2.). Если , то изокванта лежит выше и правее , и ей соответствуют такие сочетания производственных факторов, которые обеспечивают больший, чем , выпуск продукции.

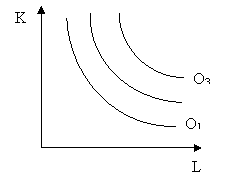Рис. 8.2. Семейство изоквант.

Аналогично, изокванта лежит выше и правее . Объемы представляют собой максимальный выпуск продукции для различных в каждом случае сочетаний труда и капитала. Кроме того, изокванты показывают три различных уровня производства расположением друг относительно друга.

Изокванты не пересекаются, и переход от выпуска к возможен только тогда, когда изменяется не только сочетание затрат труда и капитала, но и величина этих затрат. При прочих равных условиях затраты на изокванте , больше затрат на изокванте . Это свидетельствует о том, что при переходе от к остается неизменной форма производственной функции f, а значит остается неизменным способ преобразования, эффективность преобразования затрат в продукцию. Для обозначения такого процесса применяется термин "эффективность технологии", которая в данном случае остается неизменной.

Так как технология воплощена в производственной функции, то ее можно выразить и измерить параметрами функции. Поскольку речь идет не о конкретной, а о любой технологии, технологии вообще, то она называется абстрактной технологией и описывается с помощью четырех характеристик производственной функции. Рассмотренная эффективность технологии представляет первую ее характеристику.

Предпринимателю изокванта помогает выбрать при изменении факторных цен такие сочетания затрат ресурсов, которые позволяют минимизировать издержки производства и максимизировать прибыль.

4. Производство с одним переменным фактором

В зависимости от ситуации, складывающейся на рынке, производитель то расширяет, то сокращает производство. Если в краткосрочном периоде невозможно изменить объем применяемых факторов (они являются фиксированными), то можно повысить интенсивность использования последних, например, организовав еще одну рабочую смену и т. д. Состояние и параметры фиксированных факторов в краткосрочном периоде опре­делены предшествующими решениями. Если за короткий период объем используемых ресурсов увеличивается или уменьшается, они становятся переменными. Как правило, в долговременном периоде все факторы производства являются переменными.

Главная задача анализа производственного выбора в краткосрочном периоде – определить влияние изменений каждого отдельного переменного фактора на объем выпуска продукции, т. е. выявить его эффективность. Проанализируем ситуацию, когда объем капитала остается фиксированным, а затраты труда изменяются. Производственная функ­ция показывает, что с увеличением переменного фактора растет и общий продукт Q.

Общий продукт Q – это количество произведенного продукта, которое изменяется по мере увеличения использования переменного фактора.

Эффективность использования труда измеряется показателями среднего и предельного продуктов труда.

Средний продукт труда представляет собой объем продукции, приходящийся на единицу переменного фактора труд: 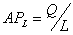. Если переменным фактором является капитал, а фиксированным труд, то средний продукт капитала .

Допустим, затраты труда увеличились на . Тогда объем производства увеличивается на , а производственная функция принимает вид: 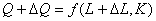. Прирост производства определяется разностью:. Рассмотрим отношение приращения продукции к вызвавшему его приращению переменного фактора , которое называется предельным продуктом тру­да , если бесконечно мало и стремится к , то стремится к бесконечно малому приращению:

,

где – представляет собой первую частную производную производственной функции по переменному фактору при фиксированном . Аналогично, при фиксированном факторе труд и переменном факторе капитал предельный продукт капитала 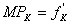. Необходимо помнить, что и представляют собой предельные про­дукты в натуральной форме. В частном случае или равны единице. Средний продукт является средней производительностью, а предельный – предельной производительностью соответствующего фа­ктора производства.

Предельный продукт труда зависит также от объема используемого фиксированного фактора, в данном случае капитала, величина которого может быть различной. Сказанное применимо и к предельному продукту капитала.

Рассмотрим взаимосвязь общего, среднего и предельного продуктов. Пусть фиксированным фактором является капитал, а труд – переменным. Построим кривую общего продукта (рис. 8.3). Для производства продукции необходимы все факторы, поскольку если =0, то и =0. Далее постепенно увеличиваем количество переменного фактора , вовлекая первую, вторую и т. д. единицы труда, считая, что увеличение выпуска обеспечивается переменным фактором, хотя это не совсем так.

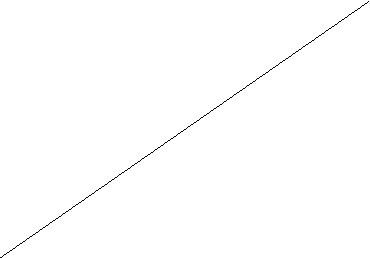
На рисунке 8.3а изображена кривая общего продукта, на которой отмечены три точки: – точка перегиба, - точка, касательная к которой совпадает с линией, соединяющей данную точку с началом координат, D - точка максимального значения ( – вспомогательная точка).

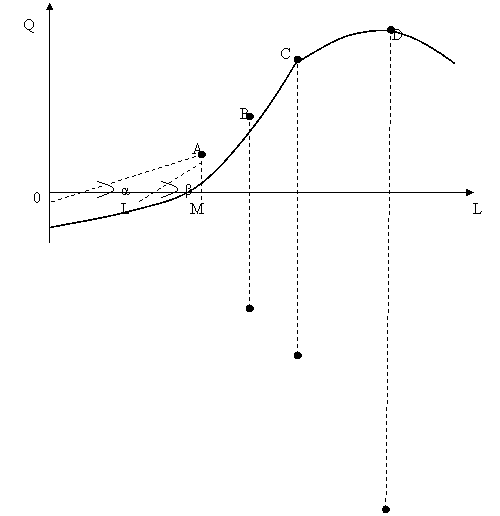
На рисунке (8.3б) показана взаимосвязь среднего продукта труда и предельного продукта труда .

Объем производства до точки увеличивается ускоряющимся темпом, так как он растет быстрее переменного фактора потому, что на каждого работника или на единицу тру­да приходится в сравнении с последующими периодами больший объем капитала. После точки темп роста общего продукта замедляется, достигает максимума в точке D и затем начинает снижаться (рис. 8.3а).

Три отрезка кривой общего продукта отражаются в кривой предельной производительности (рис. 8.3б). Предельная производительность представляет собой приращение продукта, получае­мое от использования каждой добавочной единицы переменного фактора.

Отношение = , ( – угловой коэффициент касательной к кри­вой выпуска в точке А) представляет предельный продукт, предельную произво­дительность труда:

.

а)

б)

О

Рис. 8.3. Взаимосвязь общего, среднего и предельного продуктов:

а - общий продукт; б - средняя и предельная производительность.

На отрезке ОВ предельный продукт растет потому, что по мере вовлечения в производство дополнительных работников все более полно используются производственные мощности предпри­ятия. На отрезке ВD рост числа занятых ведет к росту общего продукта (рис. 8.3а), но снижает величину предельного продукта (рис. 8.3б). Здесь соот­ношение между трудом и капиталом становится таким, что каждый последующий дополнительный работник обеспечивает меньший прирост общего объема производства, чем его предшественник. В точке D выпуск достигает максимального значения (рис. 8.3а), а приращение продукта (предельный продукт) становится равным нулю (рис. 8.3б). Когда общий про­дукт начинает снижаться, предельная производительность станови­тся отрицательной. Последнее означает, что возникает избыток переменного фактора относительно количества используемого пос­тоянного фактора.

Динамика средней производительности также отражает зависи­мость между переменными вложениями труда и объемом производства. В точке отношение общего продукта к затраченному перемен­ному фактору равно и измеряет средний продукт труда: .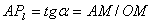

Как видно на рис. 8.3б, на отрезке ОС средний продукт растет, на отрезке CD – снижается. В точке (точка пересечения среднего и предельного продуктов) устанавливается равенство 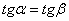и, сле­довательно, здесь средний и предельный продукты равны. Учитывая связь общего, предельного и среднего продуктов, точки В, С и D называют критическими.

Поясним, почему на отрезке ОВ кривой общего продукта предельная производительность растет быстрее, чем средняя. Напомним, что предельная производительность рас­тет только на указанном отрезке, так как использование дополнительных работников обеспечива­ет все более полное использование имеющихся мощностей. Средняя производительность по мере вовлечения в производство дополни­тельных работников изменяется следующим образом. Пока к средней добавляется предельная, превышающая предыдущие значения сред­ней производительности – средняя увеличивается. Если к средней добавляется предельная величина, которая является мень­ше любого предыдущего значения средней – средняя умень­шается.

За изменением предельной производительности фактора труд можно проследить по угловому коэффициенту касательных (наклону кривой) к кривой общего продукта. До точки В он увеличивается, после точки В уменьшается. В точке D наклон касательной к кри­вой выпуска (угловой коэффициент ) равен нулю и . За точкой D наклон кривой становится отрицательным. Таким обра­зом, на кривой общего продукта имеется один отрезок (вогнутостью вверх до точки В), где затраты первых частей переменного факто­ра приводят к более быстрому увеличению выпуска продукции и рас­тущей производительности. На другом отрезке (вогнутостью вниз от точки В и далее) имеет место убывающая производительность. Эта закономерность известна в экономической теории как закон убыва­ющей производительности. Суть его в том, что когда в производс­тве используется переменный фактор, то при неизменном состояния техники быстро достигается точка, в которой предельная произво­дительность становится убывающей.

В математической форме падение предельной производительно­сти выражается следующим образом. Производственная функция f (L,К) является возрастающей по отношению к L и К, т. е. с возрастанием переменного фактора на (или на ) объем Q увеличивается. В соответствии со свойством аддитивности имеем:

или

, так как .

При 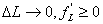. Аналогично . Производные и представляют собой предельную производитель­ность труда и капитала, т. е. дополнительную продукцию, получае­мую в результате использования дополнительной единицы одного из факторов производства. Производственная функция 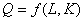име­ет убывающие предельные производительности, что выражается дос­таточным условием:

Частные производные и рассматриваются как функции. Они убывают, если 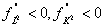, т. е. вторые частные производные отрицательны. Если , то функции и возрастают. Выполнение названных ус­ловий ниже покажем на примере функции Кобба-Дугласа.

Границы действия закона убывающей предельной производи­тельности может изменить технический прогресс. Допустим, имеют­ся три различных технических уровня производства. Каждому соот­ветствует кривая общего продукта (рис. 8.4.).

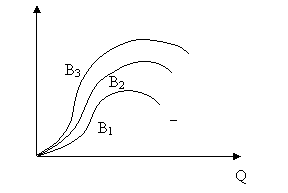Рис. 8.4. Технический прогресс и объем общего продукта.

Технический прогресс обеспечивает производство все большего объёма общего продукта, возрастающую предельную производительность до точек 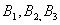(точки перегиба), после чего начинается убывание предельной производительности.

5. Замещаемость производственных факторов

Увеличение использования одного фактора производства при определенном объеме выпуска продукта всегда будет сопровождаться уменьшением количества другого фактора. Так, например, движение из точки в точку по одной изокванте не приводит к изменению объема производства, т. е. 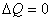(рис. 8.5). Но при этом сокращаются затраты капитала на и увеличиваются затраты труда на . Отношение показывает замещение одного фактора производства дру­гим при сохранении постоянного объема продукции и называется предельной нормой технологического замещения ().

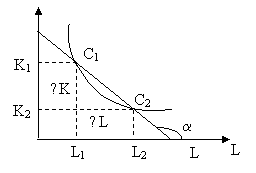Рис. 8.5. Замещаемость факторов производства.

Неред­ко используют положительную величину от­ношения 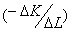. Если факторы производства бесконечно делимы, то

В рассматриваемом случае переменные факторы – аргументы производственной функции Q=f(L,K) – получают приращения и , а функция – приращение :

.

Функция получает частное приращение, если , а , т. е. остается неизменным; или если , т. е. неизменно, а . Частное приращение при равно:

,

.

Отсюда .

Полный дифференциал производственной функции dQ равен сумме частных дифференциалов:

.

В итоге получаем: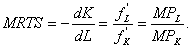

Отношение есть угловой коэффициент секущей на дуге , а абсолютное значение угло­вого коэффициента изокванты представляет собой предельную норму тех­нологического замещения труда капиталом.

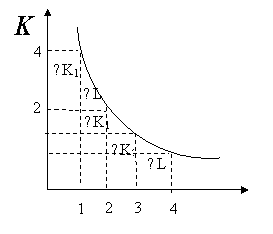
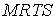уменьшается по мере движения вниз вдоль изокванты. Это означает, что кривая имеет вогнутую относительно начала ко­ординат форму, и что действует закон убывающей предельной нормы технологического замещения ресурсов (рис. 8.6.).

Ко­гда затраты труда L увеличиваются с 1 до 2 (рис. 8.6.), то происходит замещение капи­тала трудом, и затраты капитала уменьша­ются при неизменном выпуске продукции вдоль изокван­ты. Труд становится менее производительным, а использование капитала все более эффективным. И наобо­рот, когда труд замещается большим количеством капитала, отдача капитала снижается. Так, в США и Канаде на сельскохозяйственных фермах с высоким соотношением капитала к труду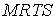 относительно низка, а в развивающихся странах с низким соотношением капитала к труду 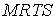высока.

L

Рис. 8.6. Убывание предельной нормы технологического замещения.

Капиталоемкость технологии определяется коэффициентом капитал/труд , от которого зависит выпуск . На рис. 8.7. представлены изокванты двух фирм с выпуском и , с одними и теми же затратами труда и разли­чными затратами капитала .

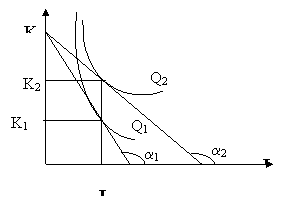Рис. 8.7. Капиталоемкость технологии.

Бо­лее высокой капиталоемкости соответствует больший объем производства >. Наклон изокванты превышает наклон , то есть , а угол образуемый касательной к изокванте с положительно направленной осью OL больше такого же угла изокванты . Это значит, что пре­дельная норма замены труда капиталом в технологии превышает предельную норму замены в технологии и 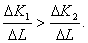Но так как 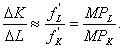, то 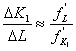, , 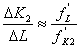и следовательно,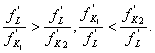

На единицу предельного продукта труда 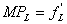предельный продукт капитала при технологии меньше, чем продельный продукт при технологии . Если к обоим производственным процес­сам добавляется единица труда, то из процесса , следует изъять меньшее количество капитала, чем из процесса , что подтверж­дает более высокую капиталоемкость процесса по сравнению с капиталоемкостью процесса .

Эластичность замены труда капиталом разработана . Производитель находится на одной и той же изокванте. Элас­тичность замены равна относительному (процентному) изменению соотношения между двумя факторами, деленному на относительное изменение предельной нормы технологического замещения. Эластич­ность замены капитала трудом и труда капиталом равны:

, .

Запишем полные дифференциалы через частные производные и дифференциалы аргументов.

Таким образом, можно говорить об эластичности замены между трудом и капиталом и определять ее по формуле:

Каков экономический смысл эластичности замены? Предпринима­тели стремятся использовать факторы производства в сочетании, которое позволяет получить наибольший общий выпуск продукции в денежном выражении. Если замена одного фактора производства другим позволяет достичь такого результата, то ее обязательно осу­ществляют. Учитывая выражение МRТS, эластичность замены в том виде, как она представлена в формуле, устанавливает зависимость между темпом роста относительных затрат факторов 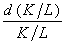и темпом роста предельной нормы замены между трудом и капиталом 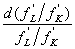, или темпом роста коэффициента относитель­ных цен факторов. Эластичность замены можно рассматривать как меру пределов осуществимости замены капитала трудом или труда капита­лом, как меру технологической «однородности» факторов производс­тва, которая оказывает влияние на выпуск продукции.

Эластичность может принимать любые значения от нуля до бес­конечности. Повышение эластичности всегда ускоряет, а понижение ее – сокращает темп роста объёма производства. Эластичность связана с конфигурацией изоквант: чем боль­ше кривизна изоквант, тем меньше эластичность замены.

6. Прямая равных издержек (изокоста)

Используя факторы производства в той или иной пропорции, производитель стремится выпустить максимальный объем продукции. Но всегда существуют ограничения: количество денег, которыми он располагает для по­купки необходимых факторов производства; цены факторов производства и , которые задаются рынком, цена производимого продукта .

Пусть – общие затраты производителя; х и у – затраты факторов производства – труда, а – капитала. и – со­ответственно, их цены. Тогда или

есть уравнение прямой, бесконечное число точек которой представ­ляет комбинации факторов, использование которых ведет к одинако­вым общим затратам. Это изокоста – прямая равных издержек (рис. 8.8), для которой выполняется условие:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7