ВЕСТНИК
МОРСКОГО
ГОСУДАРСТВЕННОГО
УНИВЕРСИТЕТА
серия
СУДОВОЖДЕНИЕ
Выпуск
Владивосток 2009
УДК 656.61.052(066)
Вестник Морского государственного университета. Вып. 5. Серия: Судовождение. – Владивосток: Мор. гос. ун-т, 2009. – 149 с.
Редакционная коллегия
, д. н. н., проф.(отв. ред.),
, к. т.н., проф. (отв. ред.),
, д. т.н., проф.,
, к. ю.н., доцент.
|
ISBN -2 |
© Морской государственный университет имени адмирала ., 2009 |
СРАВНИТЕЛЬНЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ
ДВИЖЕНИЯ СУДОВ НА ЦИРКУЛЯЦИИ В УСЛОВИЯХ МЕЛКОВОДЬЯ
, А.,
МГУ им. адм. , г. Владивосток
Одна из тенденций развития современного морского судоходства заключается в увеличении как общего, так и относительного количества крупных судов, длина которых достигает двух-трех сотен метров, что составляет один порядок с размерами многих фарватеров, узкостей, водных путей. В то же время, многие прибрежные районы, подходные пути и портовые акватории становятся соизмеримыми с параметрами циркуляции таких судов. Эта тенденция еще более обостряет проблему обеспечения безопасности мореплавания в таких районах, которые приобретают статус стесненных вод.
В постоянно меняющихся эксплуатационных условиях (загрузка судна, его осадка, глубина под килем) точное маневрирование становится чрезвычайно затруднительным. Судоводитель не имеет инструментария, с помощью которого он мог бы определить, например, на какой траектории окажется судно при повороте на новый курс при конкретном угле перекладки руля, тем более в условиях мелководья. Имеющаяся в настоящее время на судах информация о маневренных элементах, предусмотренная Резолюцией ИМО А.601(15), которая представлена, в большинстве случаев, лишь одной циркуляцией на глубокой воде при максимальном угле перекладки руля, в обычной судоводительской практике планирования и осуществления перехода является практически бесполезной и может быть использована лишь в экстренных ситуациях.
В связи с этим представляется целесообразным наличие на борту каждого крупного судна дополнительных кривых циркуляции для промежуточных углов перекладки руля и, что особенно важно, для различных отношений глубины к осадке судна. В настоящее время получение такой информации возможно лишь с помощью моделирования. В настоящей статье представлены результаты моделирования движения судов на циркуляции в условиях мелководья, которые сравниваются с данными натурных испытаний и расчетами, выполненными с применением имеющихся математических моделей.
Моделирование движения судов на циркуляции выполнено на навигационном тренажере NTPro 3000 производства фирмы Тransas Marine. Движение осуществлялось при отсутствии внешних воздействий (ветра, течения, волнения). Информация для построения циркуляций получалась следующим образом:
– на какой-либо морской навигационной карте находился нужный район, пригодный для выполнения циркуляции (для циркуляции на глубокой воде – любой район открытого моря с большими глубинами; для циркуляции на мелководье – район с ограниченными глубинами и акваторией, достаточной для циркуляции);
– на станции инструктора загружалась нужная модель с таким расчетом, чтобы можно было бы произвести циркуляцию для всех углов перекладки руля; затем задавался начальный курс, начальная скорость движения модели в тех пределах, которые соответствуют маневренным скоростям данной модели;
– выбранный для циркуляции модели судна район мелководья выделялся и ограничивался нужной глубиной;
– включались приборы, необходимые для получения данных о движении судна (GPS, эхолот, управление судном переводилось на «автомат»);
– на электронной карте выставлялся буй, вокруг которого планировалось движение судна на циркуляции;
– со станции инструктора запускалось упражнение. Модель судна начинала движение с заданным курсом и скоростью;
– на конец третьей минуты на глубокой воде, когда модель судна выходила на прямой курс, и на конец пятой минут, когда движение на прямом курсе стабилизировалось, и происходила окончательная просадка модели судна, которая зависела от глубины под килем, на станции инструктора движение останавливалось. В момент остановки движения получался «стоп–кадр», т. е. модель судна останавливалась мгновенно, поэтому была возможность снять все необходимые данные, которые в момент остановки находились в «замороженном» состоянии;
– с дисплея снимался курс (с точностью до 0.1о), линейная скорость (с точностью до 0.1 узла), глубина под килем (с точностью до 0.1 м), скорость поворота (с точностью до 0.1 град/мин.), управление судном снималось с автоматического, а руль перекладывался на нужный угол;
– с электронной карты снимались пеленг и расстояние до выставленного буя (пеленг с точностью до 0.1о, расстояние - до 0.1 м);
– производится пуск движения модели судна. В момент пуска модель продолжает движение с теми же параметрами курса и скорости, которые были зафиксированы в момент остановки. В этот же момент начинается перекладка руля на заданный угол. Модель судна начинает движение по циркуляции с заданным углом перекладки;
– в дальнейшем модели судна останавливались через каждые 10о изменения курса. Снимались те же данные, которые указаны выше, за исключением перекладки руля.
Таким образом, данные для построения циркуляций снимались с достаточной точностью, чтобы можно было бы сделать определенные выводы. Моделирование движения на циркуляции выполнялось для пяти различных судов с обычными обводами корпуса, основные характеристики которых приведены в таблице 1.
С применением стандартного пакета Excel был выполнен статистический регрессионный анализ всех данных моделирования. Процедура и некоторые результаты этого анализа представлены в работе [1]. В частности, установлено, что зависимость радиуса установившейся циркуляции на мелководье RMуст от отношения глубины к осадке судна для всех судов имеет степенной характер
RMуст = b (Н/d)С , (1)
где b – константа регрессии, с – коэффициент регрессии.
Таблица 1
Основные характеристики судов, использованных при моделировании
|
Тип модели судна |
Водоиз- мещение, т |
Длина наибольшая, м |
Ширина, м |
Осадка, м | |
|
носом |
кормой | ||||
|
Балкер |
33089 |
182.7 |
22.6 |
10.1 |
10.7 |
|
Танкер |
77100 |
242.8 |
32.2 |
12.5 |
12.5 |
|
Ро-Ро |
25400 |
184.2 |
30.6 |
8.2 |
8.2 |
|
Паром |
24841 |
230.9 |
29.2 |
8.0 |
8.0 |
|
Контейнеровоз |
132540 |
347.0 |
42.8 |
14.0 |
14.0 |
В таблице 2 сведены результаты статистического регрессионного анализа зависимости радиуса установившейся циркуляции на мелководье RMуст от отношения глубины к осадке Н/Т. Во всех случаях коэффициент парной корреляции превышает 0,94. Такие же результаты получены для выдвига и тактического диаметра циркуляции.
Таблица 2
Расчетные параметры корреляции между радиусом установившейся циркуляции на мелководье RMуст и отношением глубины к осадке Н/Т для различных судов
|
Угол перекладки руля (δ) |
10° |
15° |
20° |
25° |
30° |
35° | |
|
Константа регрессии b |
Балкер |
1211 |
1087,2 |
989,51 |
925,5 |
892,9 |
850,45 |
|
Контейнеровоз |
13885 |
8238,1 |
5543,9 |
4072,1 |
3216 |
2837,9 | |
|
Танкер |
2156,4 |
1748,8 |
1534,4 |
1350,1 |
1169,9 |
1055,1 | |
|
Паром |
1881,7 |
1467,8 |
1209 |
1053 |
903,29 |
818,51 | |
|
Ро-Ро |
5984,2 |
3981,8 |
2984,6 |
2363,4 |
1962,4 |
1611,5 | |
|
Коэффициент регрессии с |
Балкер |
-0,4216 |
-0,5115 |
-0,5547 |
-0,6293 |
-0,6997 |
-0,7591 |
|
Контейнеровоз |
-1,7724 |
-1,5432 |
-1,3904 |
-1,2881 |
-1,2325 |
-1,2355 | |
|
Танкер |
-0,4473 |
-0,4491 |
-0,4681 |
-0,4966 |
-0,4436 |
-0,4501 | |
|
Паром |
-0,466 |
-0,487 |
-0,506 |
-0,51 |
-0,52 |
-0,5541 | |
|
Ро-ро |
-1,0172 |
-0,9501 |
-0,8769 |
-0,8017 |
-0,766 |
-0,7137 | |
|
Коэффициент парной корреляции |
Балкер |
-0,9925 |
-0,9909 |
-0,9917 |
-0,989 |
-0,9895 |
-0,9933 |
|
Контейнеровоз |
-0,9939 |
-0,9871 |
-0,9828 |
-0,9642 |
-0,9446 |
-0,9812 | |
|
Танкер |
-0,9658 |
-0,9729 |
-0,9752 |
-0,9642 |
-0,978 |
-0,9944 | |
|
Паром |
-0,9553 |
-0,9462 |
-0,9533 |
-0,9642 |
-0,9445 |
-0,9649 | |
|
Ро-ро |
-0,9819 |
-0,971 |
-0,9687 |
-0,9733 |
-0,9446 |
-0,967 | |
|
Коэффициент детерминации R2 |
Балкер |
0,9852 |
0,9818 |
0,9835 |
0,9781 |
0,9792 |
0,9866 |
|
Контейнеровоз |
0,9879 |
0,9743 |
0,9704 |
0,9659 |
0,9731 |
0,9627 | |
|
Танкер |
0,9328 |
0,9466 |
0,9511 |
0,9783 |
0,9742 |
0,9888 | |
|
Паром |
0,9126 |
0,8953 |
0,9089 |
0,9296 |
0,8922 |
0,931 | |
|
Ро-ро |
0,9357 |
0,9428 |
0,9383 |
0,9473 |
0,9527 |
0,9389 |
Для определения параметров циркуляции для любого промежуточного значения угла перекладки руля δ были получены зависимости свободного члена b и коэффициента с регрессии (1), которые имеют, соответственно, логарифмический и линейный характер.
Следующий этап статистического анализа заключался в выполнении множественной регрессии, т. е. в получении такого уравнения множественной регрессии, которое бы определяло зависимость элементов циркуляции на мелководье как результативного признака от двух факторных признаков: отношения глубины к осадке судна Н/d и угла перекладки руля δ. Установлено, что эта зависимость имеет экспоненциальный характер для всех элементов циркуляции. В частности, для радиуса установившейся циркуляции на мелководье эта зависимость имеет вид:
RMуст =bm1(H/d)m2δ =1807,4∙0,8(H/d)0,98δ. (2)
где b, m1 и m2 – константа и коэффициенты регрессии, соответственно.
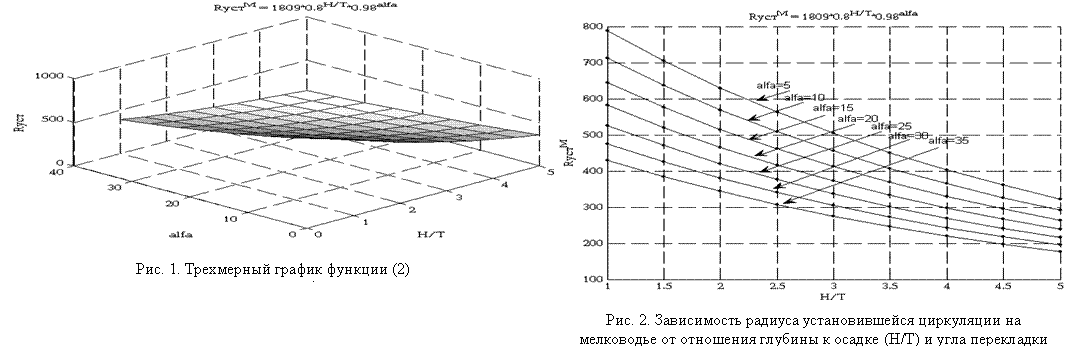 |
На рис. 1 показан трехмерный график функции (2), полученный с использованием пакета MatLab 7. Однако для практических целей более удобно использовать двухмерное представление этой функции в виде номограммы, представленной на рис. 2.
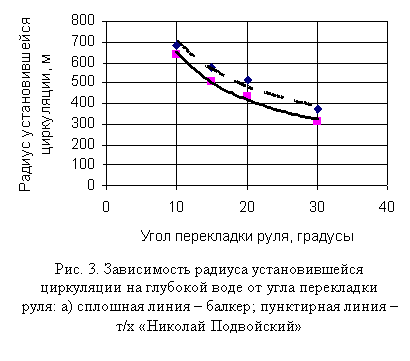 Достоверность полученных закономерностей может быть проверена путем сравнения результатов моделирования с фактическими параметрами циркуляции реальных судов. Однако такой информации достаточно мало. Так, в работе [2] представлены данные натурных экспериментов по определению параметров циркуляции т/х «Николай Подвойский», имеющего следующие основные размерения: длина наибольшая – 186,2 м; ширина наибольшая – 23,45 м; водоизмещение в полном грузу – 30810 т; осадка в полном грузу – 9,86 м, диаметр винта – 5,9 м. В графическом виде эти данные показаны на рис. 3. вместе с результатами обработки данных циркуляции балкера, основные размерения которого почти совпадают с размерениями т/х «Николай Подвойский». Из рисунка видно, что представленные зависимости практически идентичны.
Достоверность полученных закономерностей может быть проверена путем сравнения результатов моделирования с фактическими параметрами циркуляции реальных судов. Однако такой информации достаточно мало. Так, в работе [2] представлены данные натурных экспериментов по определению параметров циркуляции т/х «Николай Подвойский», имеющего следующие основные размерения: длина наибольшая – 186,2 м; ширина наибольшая – 23,45 м; водоизмещение в полном грузу – 30810 т; осадка в полном грузу – 9,86 м, диаметр винта – 5,9 м. В графическом виде эти данные показаны на рис. 3. вместе с результатами обработки данных циркуляции балкера, основные размерения которого почти совпадают с размерениями т/х «Николай Подвойский». Из рисунка видно, что представленные зависимости практически идентичны.
Десятипроцентное увеличение радиуса установившейся циркуляции т/х «Николай Подвойский» объясняется тем, что его длина на 3 метра больше по сравнению с балкером, и, главное, тем, что его осадка почти на метр превышает осадку балкера.
Проверку достоверности полученных результатов можно выполнить также путем их сравнения с данными других авторов. В специальной литературе имеются лишь две модели, определяющие влияние мелководья на элементы циркуляции, в частности, на радиус установившейся циркуляции:
модель Рейнольдса [3] 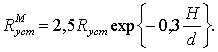 (3)
(3)
и модель Гофмана [4] 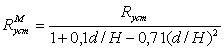 (4)
(4)
Однако обеим этим моделям присущ один и тот же недостаток: они не учитывают такие важные параметры, как угол перекладки руля и размеры судна, его осадку. Эти модели устанавливают зависимость только между радиусом установившейся циркуляции и отношением глубины к осадке судна. Хотя один и тот же радиус циркуляции может быть и у судна длиной 50 м, и у судна длиной 250 м, естественно, при разных углах перекладки руля. Тем не менее, с использованием обеих этих моделей были рассчитаны значения радиусов установившейся циркуляции при различных значениях отношения глубины к осадке применительно к двум ситуациям моделирования циркуляции балкера: при угле перекладки 10о, когда радиус установившейся циркуляции был равен 640 м, и при угле перекладки 30о, когда радиус уменьшился до 315 м. Результаты расчетов для двух значений углов перекладки руля в графическом виде представлены на рис. 4.
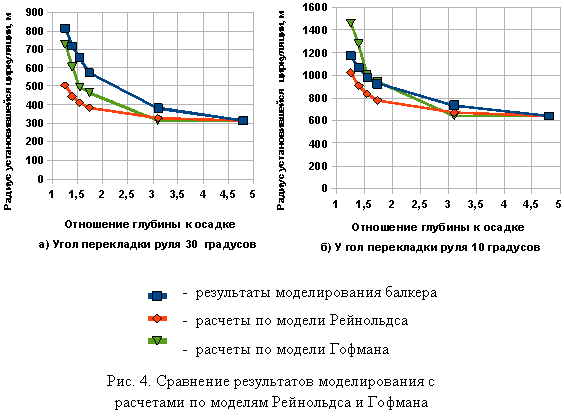
Расчеты показали, что результаты использования трех методов (моделирование, модель Рейнольдса и модель Гофмана) приближаются друг к другу при уменьшении угла перекладки руля. При этом результаты моделирования занимают примерно среднее значение между расчетами по моделям Рейнольдса и Гофмана, когда отношение глубины к осадке становится менее 2 (рис. 4, б). Однако при больших углах перекладки руля в математической модели, использованной при моделировании, влияние мелководья проявляется гораздо более выражено, чем в обеих моделях, особенно в модели Рейнольдса. По сравнению с расчетами по модели Гофмана результаты моделирования отличаются примерно на 10-15%.
Окончательные выводы о степени достоверности любого из рассмотренных методов могут дать лишь обширные натурные эксперименты, однако их проведение практически крайне маловероятно, хотя бы из-за проблем, связанных с выборов районов моря с ровным дном и соответствующими глубинами. Тем не менее, учитывая указанный выше основной недостаток моделей Рейнольдса и Гофмана, имеются все основания полагать, что зависимости, полученные на основе анализа результатов моделирования, являются вполне работоспособными и могут быть использованы в судоводительской практике при планировании и осуществлении плавания в стесненных водах.
Таким образом, на основе выполненного анализа можно сформулировать следующие выводы:
1) зависимость элементов циркуляции (радиуса установившейся циркуляции, тактического диаметра и выдвига) от угла перекладки руля и отношения глубины к осадке судна может быть выражена степенной функцией;
2) на мелководье радиус циркуляции заметно увеличивается, причем чем больше угол перекладки руля, тем больше это увеличение. В частности, для балкера при отношении глубины к осадке, равном 1,22, радиус циркуляции увеличивался в 2,8 раза при угле перекладки руля 35° и в 1,8 раза при угле перекладки руля 10°;
3) увеличение радиуса циркуляции вследствие влияния мелководья необходимо учитывать при предварительной и исполнительной прокладке при плавании в стесненных районах.
Литература
1. , Лентарёв анализ результатов моделирования движения судна на циркуляции. Вестник Морского государственного университета. Вып. 23 Серия: Судовождение. - Владвосток: Мор. гос. ун-т, 2008. - С. 58-65
2. Иванов особенности поворотливости больших танкеров. ЦБНТИ ММФ. Экспресс-информация. Серия «Безопасность мореплавания». М., 1978. - № 4(104). - С. 2-11.
3. Rejnolds J. Ship’s turning characteristics in different water depths. Safety at Sea International. 1976. – № 9
4. Гофман и расчет поворотливости судов внутреннего плавания. Л: Судостроение, 1971.
ПОГРЕШНОСТИ РАСЧЕТА ТОЧЕК ПОВОРОТА ПРИ ПЛАВАНИИ НА МЕЛКОВОДЬЕ
, А.,
МГУ им. адм. , г. Владивосток
Современные условия судоходства, среди прочего, характеризуются тем, что все большая часть ходового времени, особенно для крупных судов, приходится на плавание в стесненных районах. В этих условиях особое значение приобретает проблема надлежащего планирования рейса, что требует уже на стадии предварительной прокладки учета всех возможных факторов, которые влияют на точность плавания, и решения ряда задач, обеспечивающих наиболее точное движение судна по выбранному маршруту. К числу таких факторов и задач относятся влияние мелководья и расчет точек поворота. Помимо того, что такие задачи рекомендуются хорошей морской проктикой, их решение является обязательным условием при выполнении предварительной прокладки в соответствии с требованиями Резолюции ИМО А.893(21) «Руководство по планированию рейса». Эти требования логически вытекают из положений Конвенции ПДМНВ-78/95, где в разделе «Основные принципы наблюдения при несении ходовой вахты» говорится следующее: «Предстоящий рейс должен быть спланирован заранее с учетом всей информации, а любой проложенный курс должен быть проверен до начала рейса».
В связи с этим в данной статье предпринята попытка количественно, хотя бы в первом приближении, оценить возможные погрешности, которые могут возникнуть при планировании и выполнении поворота судна, обусловленные следующими причинами:
а) неверный расчет точки поворота (точки начала перекладки руля);
б) неучет влияния мелководья.
Отметим так же, что как в нормативных документах, так и в специальной литературе такие количественные оценки до сих пор отсутствуют.
Сначала рассмотрим ситуацию, когда для конкретных условий плавания выбран правильный радиус циркуляции, но расчет точки поворота выполнен неверно. Иными словами, неверно рассчитано расстояние упреждения (или упреждение), заключенное между точкой поворота и точкой пересечения старого и нового курсов. (В некоторых англоязычных источниках это расстояние называется «расстояние до нового курса» - distance to new course). Помимо обычного промаха в расчетах и графических построениях такая ошибка может быть вызвана применением различных методов определения точки поворота. (Анализ таких методов, оставленный за рамками данной статьи, показывает, что они дают различные результаты). Попытаемся ответить на вопрос о том, насколько судно отклонится от линии намеченного курса (пути), если судоводитель ошибется в выборе точки начала поворота. Эта ситация представлена на рис. 1. Введём следующие обозначения: РРо = ∆р – погрешность в расстоянии упреждения; CA = ∆uо – поперечное смещение с линии нового курса; АСо = ∆lо – продольное смещение по курсу; ССо = ∆со – линейное смещение от точки выхода на новый курс; < САСо = 90°; < ССоА = К2 – К1 = ∆ К – угол поворота.
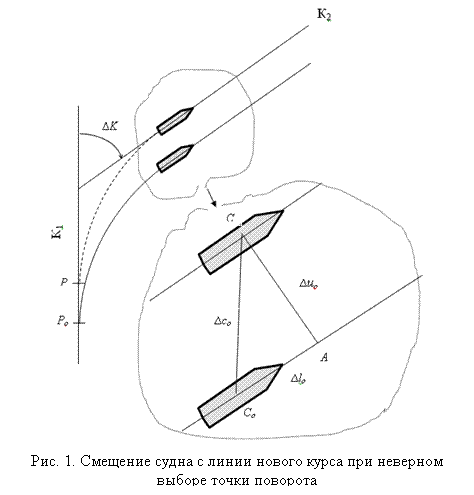 |
 Очевидно, что поперечное смещение с линии нового курса можно выразить в виде
Очевидно, что поперечное смещение с линии нового курса можно выразить в виде
∆uо = ∆со∙sin∆ К = ∆р ∙sin∆ К (1)
Тогда продольное смещение будет определяться как
∆lо = ∆р ∙cos∆ К ( 2)
Поперечное смещение ∆uо возрастает с увеличением угла поворота, достигая максимального значения, равного ∆р, при повороте на 90о, затем начинает уменьшаться и становится равным нулю, когда судно ложится на обратный курс. Продольное смещение по курсу ∆lо меняется обратным образом по сравнению с ∆uо.
Что касается линейного смещения от точки выхода судна на новый курс, то при любом угле поворота его величина равна погрешности в расстоянии до точки начала поворота судна, т. е. ∆со = ∆р, и, кроме того, совпадает с ним по направлению.
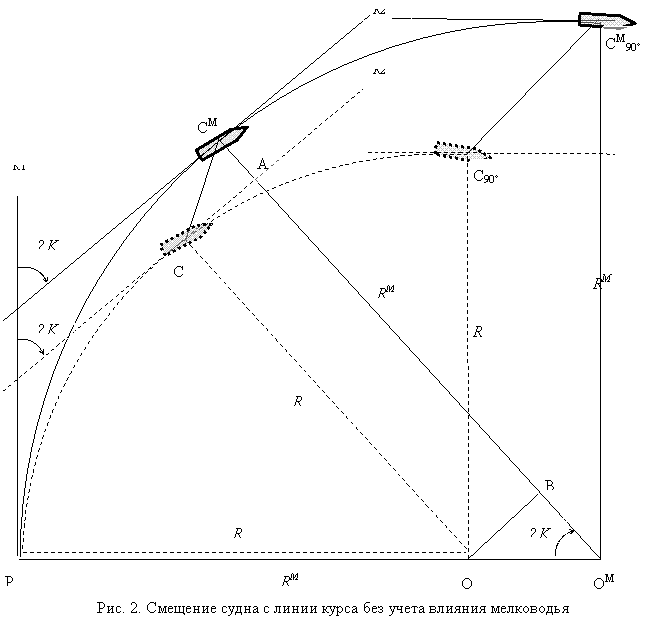
Известно, что если глубина под килем становится менее пяти осадок судна, то это начинает сказываться на характеристиках управляемости судна. В частности, увеличивается радиус циркуляции. Следовательно, этот фактор необходимо учитывать при планировании и выполнении рейса, особенно если отношение глубины к осадке становится меньше 2÷3. Рассмотрим погрешности, которые могут возникнуть, если не учитывать влияние мелководья при планировании и реализации поворотов. На рис. 2 пунктирная линия К2 – новый курс, на который нужно лечь судну. Предположим, что для этого на этапе предварительной прокладки была рассчитана точка перекладки руля таким образом, чтобы в точке Р судно начало поворот, а в точке С – вышло на новый курс. Однако под влиянием мелководья радиус циркуляции увеличивается и, фактически, судно будет двигаться по циркуляции, показанной сплошной линией. При этом судно выйдет на новый курс в точке СМ. В этом случае АСМ – поперечное смещение с линии курса (причем оно всегда направлено влево от выбранного курса при повороте вправо и наоборот), СА – продольное смещение по курсу, а ССМ – линейное смещение точки выхода на новый курс.
Если обозначить АСМ = ∆uМ, СА = ∆lо, ССМ = ∆сМ , R – радиус циркуляции, RМ – радиус циркуляции на мелководье, К2 – К1 = ∆ К – угол поворота, а также учесть, что
ООМ = RМ – R,
АC = ОБ = ООМ ∙ sin ∆ К = (RМ – R) sin ∆ К,
то после несложных преобразований получим
∆uМ = CMOM – AOM = (RМ – R)∙ (1 – cos ∆ К), (3)
![]() (4)
(4)
∆lо = (RМ – R) sin ∆ К (5)
Анализ этих зависимостей показывает, что, если при прокладке не учитывать увеличение радиуса циркуляции из-за влияния мелководья, то поперечное смещение с линии нового курса ∆uМ возрастает с увеличением угла поворота, становится равным (RМ – R) при повороте на 90о (точка CM90° на рис. 2) и достигает максимального значения, равного 2(RМ – R), когда судно ложится на обратный курс. Продольное смещение по курсу достигает максимального значения, равного (RМ – R) при повороте на 90о. Линейное смещение точки выхода на новый курс ∆сМ с увеличением угла поворота также возрастает, при повороте на 90о достигает значения, равного ![]() , при дальнейшем повороте судна продолжает увеличиваться и при выходе судна на обратный курс становится равным как ∆uМ как по величине, так и по направлению, фактически совпадая с последним.
, при дальнейшем повороте судна продолжает увеличиваться и при выходе судна на обратный курс становится равным как ∆uМ как по величине, так и по направлению, фактически совпадая с последним.
Следует полагать, что при совместном действии двух рассмотренных факторов – а) неверном расчете точки перекладки руля и б) неучете или неверном учете влияния мелководья – общие значения как поперечного (∆u), так и линейного (∆с) и продольного смещения (∆l) будут равны сумме обоих составляющих, т. е.
∆u = ∆uо + ∆uМ , (6)
∆с = ∆со + ∆uМ, (7)
∆l = ∆lо + ∆lМ , (8)
где слагаемые рассчитываются таким же образом, как и при раздельном действии рассмотренных факторов.
Следовательно, если не учитывать влияние мелководья, то ошибки в планируемом и фактическом местоположении судна могут достигать нескольких кабельтовых, а то и более мили (см. предыдущую статью в этом сборнике). Такие ошибки при плавании в стесненных районах недопустимы.
Может возникнуть вопрос о правомерности рассмотренных закономерностей и достоверности полученных оценок, например, из-за того, что в реальности во время маневренного и эволюционного периодов циркуляция имеет переменный радиус кривизны. Однако здесь встает проблема расчета мгновенного радиуса кривизны эволюционной части циркуляции, а полученные соотношения остаются справедливыми и в этом случае. В то же время, проблему расчета мгновенного радиуса можно решить, если эволюционную часть циркуляции аппроксимировать в виде Архимедовой спирали. Тогда радиус кривизны любой точки эволюционной части циркуляции RЭ можно рассчитать следующим образом:
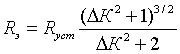 . (9)
. (9)
Следует отметить, что влияние мелководья следует учитывать и при расчете координат точки не возврата. В этом случае из-за многообразия очертаний береговой черты, опасных изобат и т. п. получить каких-либо количественных соотношений для оценки возможной ошибки невозможно, однако в любом случае учет увеличения радиуса циркуляции за счет влияния мелководья будет приводить к тому, что точка не возврата будет находиться мористее побережья.
Таким образом, можно сделать следующие выводы:
1) при наличии погрешности в расстоянии упреждения расчетное положение судна будет смещено относительно его фактического положения, и величина этого смещения может достигать максимального значения, равного погрешности в упреждении;
2) если при расчете точки поворота в условиях мелководья не учитывать увеличение радиуса циркуляции, то расчетное положение судна будет смещено относительно его фактического положения, и величина этого смещения может достигать максимального значения, равного почти полуторной разнице между расчетным и фактическим значениями радиуса циркуляции;
3) при наличии двух рассмотренных факторов (погрешность в расстоянии упреждения и не учет влияния мелководья) общая погрешность в местоположении судна равна сумме обеих составляющих.
Это обстоятельство необходимо учитывать при планировании маршрута плавания, особенно для крупных судов.
СИСТЕМАТИЗАЦИЯ ВЫРАЖЕНИЙ ДЛЯ РАСЧЕТА И РЕЗУЛЬТАТЫ
РАСЧЕТОВ ОСНОВНЫХ ПАРАМЕТРОВ ГИРОАЗИМУТКОМПАСА «ВЕГА» ПО РЕЗУЛЬТАТАМ ОБРАБОТКИ КРИВЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
, , ёсов,
МГУ им. адм. , г. Владивосток
Произведена систематизация выражений для расчета основных параметров корректируемого гироазимуткомпаса «Вега-С» с цифровой системой управления, приведены величины основных параметров гироазимуткомпаса, полученные в результате обработки экспериментальных кривых затухающих колебаний и произведено сравнение экспериментальных и теоретических величин параметров для широты г. Владивостока.
В настоящее время общепризнано, что необходимо решать комплекс крупных научно-технических проблем по повышению безопасности плавания в современных условиях судоходства. В общем комплексе проблем немаловажным является разработка автономных пассивных систем навигации, к которым относятся гирокурсоуказатели, и методов их использования.
Рост тоннажа, скоростей, количества транспортных и промысловых судов привели к увеличению интенсивности судоходства. В связи с этим возросли требования к технико-эксплуатационным характеристикам гирокомпасов, информация от которых, совместно с данными от судовых измерителей скорости и пройденного расстояния, позволяет вести непрерывное и, притом, автономное счисление. Информация о курсе судна также используется для исключения методических погрешностей других технических средств навигации: радиолокационных станций навигации и систем автоматической радиолокационной прокладки расхождения судов, спутниковых и радионавигационных систем, инерциальных навигационных систем.
Среди гирокурсоуказателей отечественный корректируемый гироазимуткомпас (ГАК) «Вега-М» занимает ведущие позиции по количеству установленных комплектов на отечественном транспортном (морском и речном) и рыболовном флотах, а также точности выработки курса.
Принципиально корректируемые ГАК имеют возможность решать следующие задачи [1]:
– ускоренное приведение в меридиан, для чего необходимо уменьшить период незатухающих колебаний ![]() на время пуска;
на время пуска;
– получение приемлемой точности курсоуказания при маневрировании, для чего нужно увеличить период ![]() .
.
К существенным недостаткам ГАК «Вега-М», которые в основном вытекают из давности разработки самого ГАК, можно отнести:
– аналоговая схема управления переходными процессами ГАК без возможности перенастройки;
– длительное время прихода в меридиан (3–6 часов);
– электромеханическая система выработки корректирующих сигналов.
В лаборатории технических средств навигации кафедры технических средств судовождения Морского государственного университета им. адм. была произведена глубокая модернизация ГАК «Вега-М». В результате без существенных изменений осталась только гиросекция (в ней СКВТ курса заменен на цифровой энкодер).
Целью работы является систематизация материалов по основным расчетным формулам для параметров ГАК «Вега-М», обработка на основе этих формул кривых затухающих колебаний модернизированного ГАК «Вега-С», полученных экспериментальным путем, и сравнения полученных результатов с теоретическими для широты г. Владивостока (место установки ГАК «Вега-С»).
Принцип работы ГАК и теоретическая база достаточно полно изложены в работах [2–5].
Для оценки основных параметров ГАК при стендовых испытаниях использовались следующие выражения:
Уравнение для угла отклонения в азимуте ![]() [3]
[3]
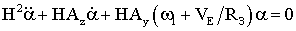 (1)
(1)
или в нормальном виде![]()
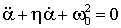 , (2)
, (2)
где 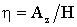 ,
, 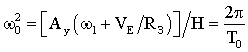 .
.
Уравнение в форме Лапласа записывается в виде
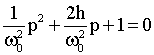 , (3)
, (3)
где 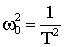 и
и 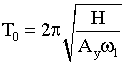 ,
,
или 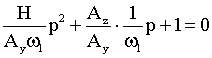 . (4)
. (4)
Уравнения (1–4) описывают переходной процесс инерционного звена второго порядка [6]
![]() , (5)
, (5)
где Т1 и Т2 – постоянные времени звена. Уравнение (5) можно представить в другом виде:
![]() , (6)
, (6)
где ![]() ,
, 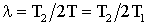 . l – коэффициент демпфирования (показатель затухания),
. l – коэффициент демпфирования (показатель затухания),
![]() .
.
Постоянная времени звена равна [6]
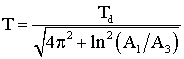 . (7)
. (7)
Переходная функция звена при подаче на вход единичного ступенчатого воздействия (отклонения оси чувствительного элемента ГАК из меридиана) и нулевых начальных значениях имеет вид
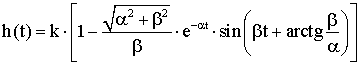 , (8)
, (8)
где 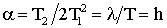 ,
, 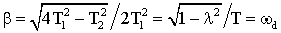 – соответственно вещественная и мнимая части корней (5) или характеристического уравнения (6), h – коэффициент затухания,
– соответственно вещественная и мнимая части корней (5) или характеристического уравнения (6), h – коэффициент затухания, ![]() – частота затухающих колебаний оси чувствительного элемента ГАК. Постоянные времени звена можно представить в виде:
– частота затухающих колебаний оси чувствительного элемента ГАК. Постоянные времени звена можно представить в виде:
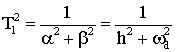 ,
, 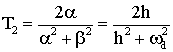 . (9)
. (9)
Для вычисления коэффициента затухания и частоты затухающих колебаний по результатам эксперимента можно воспользоваться выражениями:
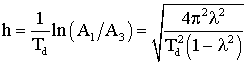 ,
, 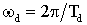 , (10)
, (10)
Td – период затухающих колебаний, А1 и А3 – амплитуды двух соседних полуколебаний одного знака относительно установившегося значения.
Из уравнений (1–3) можно получить:
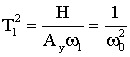 ,
, 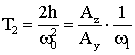 , (11)
, (11)
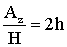 ,
, 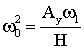 ,
, 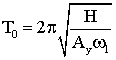 . (12)
. (12)
Фактор затухания вычисляется по формулам [2]
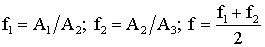 . (13)
. (13)
Показатель затухания, коэффициент, связь между периодами незатухающих и затухающих колебаний и частота затухающих колебаний соответственно равны:
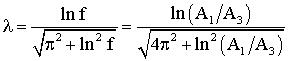 ,
,
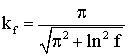 ,
, 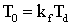 , (14)
, (14)
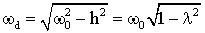 .
.
Аналитическая формула переходной характеристики инерционного звена второго порядка имеет вид [3]
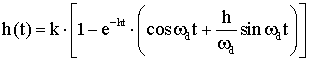 , (15)
, (15)
которая аналогична формуле (8).
Дублирование выражений для некоторых параметров введено для сравнительного анализа величин полученных по различным формулам.
В таблице 1 приведены величины основных параметров ГАК «Вега-М» для широты г. Владивостока (![]() ).
).
Таблица 1
Основные параметры ГАК «Вега-М»
|
Обозначение |
Наименование |
Значение |
Размерность |
|
Н |
Кинетический момент гироскопа |
0,4 |
Н·м·с |
|
|
0,045 | ||
|
|
0,0171 |
1/с | |
|
|
0,00077 |
1/с | |
|
|
Угловая скорость вращения Земли |
7,29·10-5 |
1/с |
|
Tg |
Постоянная времени ИГ |
60 |
с |
|
Ay |
Модуль управляющего момента |
6,84·10-3 |
Н·м/рад |
|
Az |
Модуль демпфирующего момента |
3,08·10-4 |
Н·м/рад |
|
|
Степень демпфирования (коэффициент затухания) |
0,38·10-3 |
1/с |
|
f |
Фактор затухании в φ=0, 60, 80 градусов |
3, 6, 30 | |
|
Т0 |
Для широты Владивостока |
6586/110 |
с/мин |
|
Тd |
Для широты Владивостока |
7198/120 |
с/мин |
|
kf |
T0/Td |
0,915 |
Вид кривой затухающих колебаний (КЗК), полученной в результате эксперимента, и её основные показатели показан на рис. 1. Второй график показывает переходной процесс индикатора горизонта.
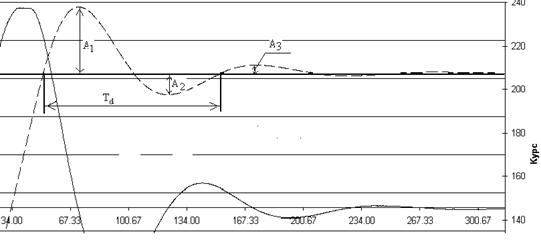
Рис. 1. Кривая затухающих колебаний
Используя выражения (3), (6) – (14) обработаны кривые затухающих колебаний. Результаты обработки сведены в таблицу 2.
Таблица 2
Результаты эксперимента
|
Параметры Дата |
k, град. |
A1, град. |
A2, град. |
A3, град. |
Td1, сек. |
Td2, сек. |
|
11.02.09 |
90 |
30,28 |
10,04 |
3,56 |
6130 |
6330 |
|
12.02.09 |
80 |
26,4 |
9,64 |
2,38 |
6231 |
5873 |
|
16.02.09 |
106 |
36,16 |
11,14 |
4,41 |
6065 |
6290 |
|
17.02.09 |
107 |
36,83 |
11,73 |
3,82 |
6150 |
6060 |
|
18.02.09-1 |
90 |
29,42 |
9,85 |
3,32 |
6100 |
6060 |
|
18.02.09-2 |
35 |
34,33 |
11,07 |
3,72 |
6100 |
6020 |
|
19.02.09-1 |
47 |
16,33 |
5,4 |
1,85 |
6035 |
6040 |
|
19.02.09-2 |
100 |
34,26 |
11,24 |
4,05 |
6095 |
6225 |
|
Среднее |
6113 |
6112 | ||||
|
10.03.09 |
135 |
33,28 |
8,42 |
2,02 |
7200 |
6980 |
Таблица 3
Результаты расчетов
|
Параметры Дата |
h, с-1 х10-4 |
ωd, с-1 х10-3 |
λ |
T1=T, сек |
T2, сек |
T0, сек. |
f |
kf |
|
11.02.09 |
3,492 |
1,025 |
0,323 |
923,5 |
595,7 |
5802 |
2,92 |
0,947 |
|
12.02.09 |
3,862 |
1,008 |
0,358 |
926,1 |
662,4 |
5808 |
3,39 |
0,932 |
|
16.02.09 |
3,469 |
1,036 |
0,318 |
915,3 |
581,3 |
5748 |
2,89 |
0,948 |
|
17.02.09 |
3,685 |
1,022 |
0,339 |
920,8 |
624,8 |
5784 |
3,1 |
0,941 |
|
18.02.09-1 |
3,577 |
1,03 |
0,328 |
917,0 |
601,7 |
5760 |
2,98 |
0,945 |
|
18.02.09-2 |
3,643 |
1,03 |
0,333 |
915,3 |
610,4 |
5748 |
3,04 |
0,943 |
|
19.02.09-1 |
3,609 |
1,041 |
0,327 |
907,5 |
594,4 |
5700 |
2,97 |
0,945 |
|
19.02.09-2 |
3,503 |
1,031 |
0,322 |
918,5 |
591,1 |
5772 |
2,0 |
0,947 |
|
Среднее |
3,605 |
1,0279 |
0,331 |
918,0 |
607,7 |
5766 |
2,91 |
0,944 |
|
10.03.09 |
3,981 |
0,8727 |
0,407 |
1047 |
852,5 |
6576 |
4,06 |
0,913 |
Таблица 4
Результаты расчетов
|
Параметры Дата |
Ay, Н∙м/рад х10-3 |
Az, Н∙м/рад х10-4 |
Az/Ay |
|
|
Td, сек |
|
|
|
Среднее |
8,923 |
2,884 |
0,032 |
1,068 |
0,767 |
6120 |
1,176 |
1,142 |
|
10.03.09 |
6,86 |
3,185 |
0,046 |
0,967 |
0,997 |
7090 |
1,015 |
1,01 |
Усреднённые вычисленные параметры модернизированного ГАК «Вега» не соответствуют параметрам серийного ГАК «Вега-М». После пересчета коэффициентов передачи по горизонтальному и вертикальному каналам получены экспериментальные данные за 10 марта 2009 г.
Вид экспериментальной кривой затухающих колебаний за 10.03.09 г. и рассчитанных по формулам (8) и (15) переходных процессов показан на рис. 2. Несовпадение кривых на начальном участке объясняется следствием того, что после режима «Горизонтирования» ГАК был выведен ускоренно из меридиана, а затем переведен в режим «Работа». Индикатор горизонта длительное время находился на упоре (t =25¸75 мин.), что исказило переходной процесс в начальный период.
Из таблицы 3 (эксперимент за 10.03.09) видно, что отклонения экспериментальных результатов от теоретических не превышает 3,3% по параметру Az и примерно 1% по остальным нормируемым параметрам, что вполне приемлемо для инженерных расчетов.
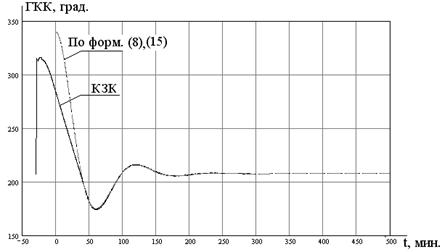
Рис.2. Вид экспериментальной КЗК и рассчитанных переходных процессов ГАК
Список использованных источников
1. Новые технические средства судовождения [Текст] / и др. Под общ. Ред. . – М.: Транспорт, 1973. – 264 с.
2. Коган, гироазимуткомпас «Вега» [Текст] / , . – М. : Транспорт, 1983. – 200 с.
3. Смирнов, средства судовождения: Теория: Учебник для вузов [Текст] / , , / Под ред. . – М.: Транспорт, 1988. – 376 с.
4. Блинов, приборы: Учебник для вузов ММФ [Текст] / , , . – 4-е изд., перераб. и доп. – М.: Транспорт, 1980. – 448 с.
5. Перминов, параметров двухрежимного корректируемого гирокомпаса [Текст] / Приборостроение, сб. научн. тр. № 000. Пермь: 1974. – С. 30–34.
6. Власенко, электроавтоматика [Текст] / , . М. : Транспорт, 1983. – 258 с.
ГИРОАЗИМУТКОМПАС «ВЕГА»
С АПЕРИОДИЧЕСКИМ ХАРАКТЕРОМ ПРИХОДА В МЕРИДИАН
, , ёсов,
МГУ им. адм. , г. Владивосток
Приводятся экспериментальные данные апериодического процесса прихода в меридиан корректируемого гироазимуткомпаса «Вега-С» с цифровой системой управления. Модули маятникового и демпфирующего моментов рассчитаны по заданным фактору затухания и времени прихода в меридиан.
В лаборатории технических средств навигации кафедры технических средств судовождения Морского государственного университета им. адм. была произведена глубокая модернизация гироазимуткомпаса (ГАК) «Вега-М». Разработана цифровая система управления гироблоком. Без существенных изменений осталась только гиросекция (в ней СКВТ курса заменен на цифровой энкодер).

|
Из за большого объема эта статья размещена на нескольких страницах:
1 2 3 4 5 6 7 |




