Вестник морского государственного унивеситета (стр. 3 )

Таблица 1.

Полученные за различные периоды наблюдений постоянные погрешности и СКП координат

Анализ табл. 1 позволяет сделать следующие выводы.

1. Непрерывных наблюдений в течение одной недели явно недостаточно для обеспечения достаточной сходимости широты и возвышения антенны. Из таблицы следует, что наибольшая скорость сходимости наблюдается у долготы.

2. Наименьшая постоянная погрешность зарегистрирована у широты (0,362 м к северу от истинной широты). Истинная широта находится внутри СКП. Наименьшая СКП зарегистрирована у долготы. Но постоянная погрешность долготы (1,378 м к востоку от истинной долготы) почти на 40 см превосходит СКП.

3. Необходимо выполнить исследования для оценки параметров низкочастотных компонент колебаний координат GPS-приёмников. Это позволит более обоснованно подойти к определению достаточной продолжительности экспериментальных наблюдений для достижения сходимости с заданной точностью.

Литература

1. Гурский вероятностей с элементами математической статистики. – М.: Высшая школа, – 328 с.

2. Комаровский точности Навстар GPS без режима избирательной доступности // Современные технологии судовождения на базе систем электронной картографии и спутниковой навигации. Материалы регионального научн.-практ. семинара. – Владивосток.: ДВГМА, 2001. – С. 83 – 92.

3. Комаровский точности НАВСТАР GPS без режима избирательной доступности // Современные технологии судовождения на базе систем электронной картографии и спутниковой навигации. Материалы регионального научн.-практ. семинара. – Владивосток.: ДВГМА, 2001. – С. 83 – 92.

4. Комаровский модели погрешностей определения места судна приёмником СРНС НАВСТАР GPS // Транспортное дело России, специальный выпуск № 2. Москва, 2004. – С. 15 – 19.

5. Гнеденко теории вероятностей. Изд. 5-е, стереотипное. – М.: Наука, 1969. – 400 с.

АНАЛИЗ ТОЧНОСТИ ПРОГНОЗА ПЕРЕМЕЩЕНИЯ ЦИКЛОНА

МЕТОДОМ ФОРМАЛЬНОЙ ЭКСТРАПОЛЯЦИИ С ПРИМЕНЕНИЕМ СГЛАЖИВАНИЯ РАЗЛИЧНЫХ ПАРАМЕТРОВ ДВИЖЕНИЯ

СПОСОБОМ НАИМЕНЬШИХ КВАДРАТОВ

, ,

НГАВТ, г. Новосибирск

Выполнена оценка точности прогноза перемещения произвольно выбранных циклонов северной части Тихого океана по японским картам приземного анализа ASAS. Прогноз осуществлён методом формальной экстраполяции движения циклонов за несколько предшествующих сроков наблюдений. Применено сглаживание параметров наблюдённого движения способом наименьших квадратов с одновременным получением уравнения регрессии, которое используется для получения прогностического значения параметров движения. Рассмотрены способы прогноза по «мгновенным» курсам и скоростям циклонов, по координатам позиций циклонов с получением линейного и нелинейного уравнения регрессии. Статистическим методом (пока на ограниченном объёме материала) установлено, что наилучшие результаты по точности даёт уравнение регрессии по координатам позиций (прогноз траектории движения).

Несмотря на значительные успехи последних лет в распространении, получении, доступности, разнообразии аналитической и прогностической гидрометеоинформации (ГМИ), собственный анализ гидрометеообстановки судоводительским составом в условиях мостика судна был и остаётся актуальной задачей. Особую актуальность такой анализ имеет на судах смешанного (река – море) плавания в силу их меньшей мореходности и значительно большей гидрометеозависимости.

Анализ синоптической ситуации предполагает выделение определяющего синоптического объекта (СО), в ветро-волновом поле которого находится судно или будет находиться в ближайшее время. Эта работа автоматически предполагает выполнение собственными силами прогноза движения определяющего СО на нужную заблаговременность, не всегда совпадающую со сроками официальных прогнозов.

Среди известных методов прогноза синоптической обстановки, пожалуй, единственно доступным в судовых условиях (подразумевается возможность либо ручных вычислений с помощью калькулятора, либо наличие персональных ЭВМ, достаточно широко распространённых на современных судах) является метод формальной экстраполяции. Традиционно на судах он применяется в графическом виде, [1], но в [2] авторам удалось показать, что точность графической работы на факсимильных картах принимаемого масштаба низка, требует сглаживания и перехода от графической работы к аналитическим вычислениям. Там же показан способ перехода к аналитике введением относительной системы координат разность широт Δφ - отшествие Δω с центром в начальной наблюдённой точке СО, а также разработана технология сглаживания наблюдённых параметров движения СО на основе способа наименьших квадратов с получением различного вида уравнений регрессии.

Для статистической проверки точности различных способов прогноза движения СО, представленных в [2], проделана следующая работа. По подборке японских факсимильных карт приземного анализа ASAS за январь – март 2006 г. на все сроки наблюдений (с незначительными пропусками) составлена таблица расположения и состояния идентифицированных синоптических объектов (здесь не приводится), в которой на каждый срок наблюдений представлен каждый сколько-нибудь значительный для мореплавания пронумерованный синоптический объект (циклон или антициклон) с регистрацией атмосферного давления в его центре, координат центра, числа замкнутых и сопряжено-замкнутых изобар. Это позволило изучить движение и эволюцию каждого из выделенных СО. Фрагмент таблицы движения СО, использованный для анализа в настоящей статье, представлен в табл.1 (выбраны только циклоны с продолжительностью существования не менее 8 сроков наблюдений). Приведённые в ней величины , , а также направления перемещения циклонов Кi j между сроками наблюдений и скорости Vi j определялись следующим образом:

Таблица 1

Фрагмент таблицы движения синоптических объектов, использованной для анализа точности прогноза перемещения СО

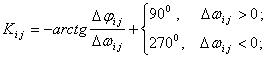
(1)

Здесь i - номер срока наблюдений СО, j – порядковый номер СО.

Размерность курса циклона Кij [градус], размерность скорости циклона Vi j [градус/6 часов] или [градус/1 срок наблюдений].

Аналогом графических построений для прогноза движения СО является аналитическое использование значений Кi j и Vi j , которое нужно сгладить и представить в виде аналитической зависимости (регрессии).

Как показано в [2], наилучшая точность сглаживания обеспечивается при использовании количества сроков наблюдений, соответствующих целым суткам, т. е. по четыре наблюдения в сутки.

Вид функции регрессии можно выбирать, исходя из характера изменения К и V , однако, даже при четырёх наблюдениях, используемых для получения регрессии, трудно установить вид функции. Использование же большего числа наблюдений существенно ограничивает возможности метода экстраполяции в судовых условиях. Поэтому достаточно оправдано применение линейной функции регрессии вида

(2)

К тому же, даже линейная зависимость K и V от времени обеспечивает получение криволинейной траектории движения СО.

Применение способа наименьших квадратов к функциональным зависимостям (2) позволяет получить следующие выражения коэффициентов регрессии, [2]:

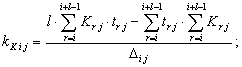
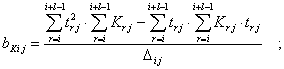
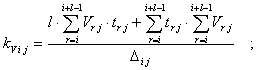
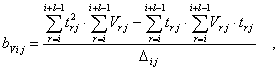(3)

где i = 2, … , nj – l - 1;

ti j = 6 (i – 1) j , часы, - время, соответствующее i-му сроку

наблюдения;

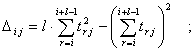
l – количество сроков наблюдений, за которое формируется уравнение регрессии ; здесь принято l = 4.

Полученные для каждого значения j, l, i линейные зависимости курса и скорости циклона вида (2) могут быть использованы для прогноза движения циклона по следующему алгоритму:

(4)

Здесь q = i+ l, … , nj.

Полученные прогностические координаты СО можно сравнить с фактическими координатами СО на соответствующее время и определить ошибку прогноза:

(5)

Пример результатов расчёта прогноза движения СО указанным способом представлен в табл. 2.

Другой способ прогноза движения СО заключается в непосредственной аппроксимации начальных l наблюденных относительных координат СО Δφ, Δω и в использовании полученной линейной или нелинейной регрессии для прогноза. Удобно искать регрессию относительных координат Δφ, Δω в параметрической форме:

Таблица 2

Пример результатов расчёта прогноза движения циклонов из табл. 1 по алгоритму (2-5). iН = 2 l = 4

- для нелинейной регрессии в виде

(6)

- для линейной регрессии в виде

, (7)

где способом наименьших квадратов можно получить для нелинейной регрессии (6)

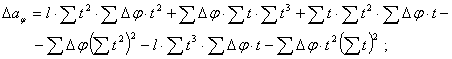
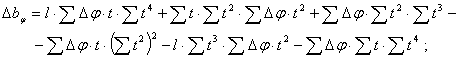
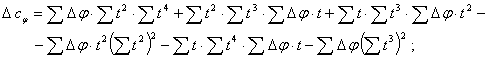
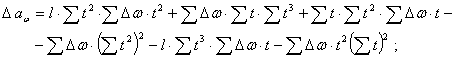
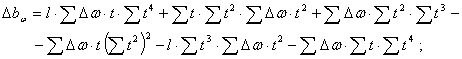
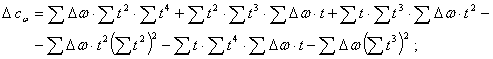
(8)

для линейной регрессии (7)

(9)

Здесь все опущенные индексы сумм означают суммирование по всем последовательным j ; от i = 1 до .

Полученную регрессию (6,8) или (7,9) также можно использовать для прогноза движения СО, принимая t = tq, j , где q = i + l,… , nj , вычисляя ошибку прогноза по (5).

Пример результатов прогноза по (7,9) при l = 4 представлен в табл. 3.

Заметим, что некоторое преимущество прогноза по относительным координатам Δφ, Δω состоит в том, что прогноз можно давать уже после четвёртого наблюдения, в то время как прогноз по курсам и скоростям СО возможен только после пятого наблюдения ( при аппроксимации по l = 4 наблюдениям).

Итоговые результаты ошибки нелинейного прогноза по курсам и скоростям СО представлены в табл. 4.

Таблица 4

Средняя ошибка нелинейного прогноза движения

циклонов по формулам (2-5) при l = 4

Итоговые результаты ошибки линейного прогноза по координатам СО представлены в табл.5.

Таблица 5

Средняя ошибка линейного прогноза движения

циклонов по формулам (7,9) при l = 4

Таблица 3

Пример прогноза траектории движения циклонов методом линейной экстраполяции Δφ, Δω

iн = 1 l = 4

продолжение таблицы 3

Принятый способ аппроксимации l наблюдённых параметров, когда параметр суммирования r проходит l значений i из имеющегося ряда nj, позволяет получить оценку точности прогноза на разных стадиях движения циклона, которые обладают известной «капризностью». Так, циклоны, зародившиеся на западной окраине рассматриваемого района Тихого океана, сначала имеют тенденцию незначительно изменять направление движения по часовой стрелке, имея общий тренд движения к востоку, а затем против часовой стрелки с постепенным замедлением разворота. На эту особенность начального этапа движения заметно реагируют все методы формальной экстраполяции, особенно нелинейной. При этом аппроксимация наблюдений, приходящихся на предшествующий смене направления разворота этап движения циклона, даёт наименее точный прогноз, ухудшающий общую статистическую картину точности прогноза. Тем не менее, сравнение данных табл. 4 и 5 показывает, что средние ошибки СОШ линейного прогноза по относительным координатам Δφ, Δω значительно ниже, чем средние ошибки нелинейного прогноза по курсам и скоростям СО. К тому же, вычислительный процесс линейного прогноза проще, а прогноз возможен при меньшем числе наблюдений.

Список литературы

1.  Сичкарёв в судовождении гидрометеорологической информации /ёв. – Новосибирск: НГАВТ, 2000. – 176 с.

2.  Сичкарёв движения циклона и относительного перемещения судна в его ветро-волновом поле /ёв, , . – Новосибирск: НГАВТ, 2008. – 101 с.

АВТОМАТИЗИРОВАННОЕ РАБОЧЕЕ МЕСТО СУДОВОДИТЕЛЯ

НА ОСНОВЕ ТЕЛЕКОММУНИКАЦИОННОЙ СЕТИ ЕСИМО

,

МГУ им. адм. , г. Владивосток

Бурное развитие компьютерных технологий остро поставило вопрос об интеграции программного обеспечения персональных компьютеров и технических средств с информационными ресурсами компьютерных сетей и создании на этой основе автоматизированных рабочих мест (АРМов) для различных специальностей, в том числе и для судовождения.

Автоматизированное рабочее место, или, в зарубежной терминологии, «рабочая станция» (work-station), - индивидуальный комплекс технических и программных средств, предназначенный для автоматизации профессионального труда специалиста и обеспечивающий подготовку, поиск и выдачу на экран, и печать необходимых ему документов и данных.

Автоматизированное рабочее место обеспечивает оператора всеми средствами и информацией, необходимыми для выполнения определенных функций. В судовождении это может быть комплексное обеспечение судоводителя корректурными материалами, информацией о портах захода, навигационных и погодных условиях предстоящего рейса для составления и корректуры рейсового плана и перехода судна по заданному маршруту.

Информационное обеспечение морской деятельности в первую очередь предусматривает поддержание и развитие глобальных информационных систем. В России к таким системам относится единая система информации об обстановке в Мировом океане (ЕСИМО).

ЕСИМО - единая виртуальная телекоммуникационная государственная сеть освещения надводной и подводной обстановки Мирового океана, создаваемая в целях интеграции и рационального использования систем, комплексов и средств различного ведомственного подчинения на базе сил и средств Министерства обороны Российской Федерации, Федеральной службы России по гидрометеорологии и мониторингу окружающей среды и других заинтересованных федеральных органов исполнительной власти Российской Федерации.

Нормативной основой ЕСИМО служат следующие документы:

-  Закон об информации и информатизации;

-  Закон о международном информационном обмене;

-  Закон об информационной безопасности;

-  Морская доктрина РФ;

Из за большого объема эта статья размещена на нескольких страницах: 1 2 3 4 5 6 7