Выходной вектор Z: масса (расход) полученного клинкера; характеристики клинкера; параметры отводимых газов.
Сложность объекта, неопределенность большинства параметров и их взаимосвязей, указывают на целесообразность прибегнуть для решения задачи управления к методам имитационного моделирования.
К наиболее популярным системам имитационного моделирования относятся AnyLogic, Aimsun, Arena, GPSS, ИМИТАК, , РДО, PTV, Tecnomatix Plant Simulation, NS-2, Transyt, Vision VISSIM, eM-Plant, Powersim.
Моделирование технологических процессов термической обработки цементного клинкера проведено в диссертации с использованием системы имитационного моделирования РДО (РЕСУРСЫ – ДЕЙСТВИЯ – ОПЕРАЦИИ), которая позволяет более глубоко и точно учитывать особенности динамики объекта автоматизации. В среде РДО удобно не только проводить имитационное моделирование технологического процесса, но и проводить анимацию для наблюдения его хода в реальном времени, что немаловажно при решении задач оптимизации управления.
Сложная динамическая система на концептуальном уровне представляется в виде множества некоторых взаимодействующих между собой ресурсов.
Ресурс — это элемент сложной системы, внутренней структурой которого можно пренебречь, в то время как его наличие и свойства как целого важны для целей описания.
Все ресурсы Сложных Дискретных Систем (СДС) образуют некоторое множество:
![]() , (22)
, (22)
где: ri — i-ый ресурс СДС, а N(t) — число ресурсов СДС в данный момент времени. Основным составляющим СДС, каковыми являются ее элементы, производственный процесс, законы функционирования, соответствуют следующие информационные объекты: ресурсы, действия, нерегулярные события и операции. Представление СДС в РДО-методе показано на рис.5.
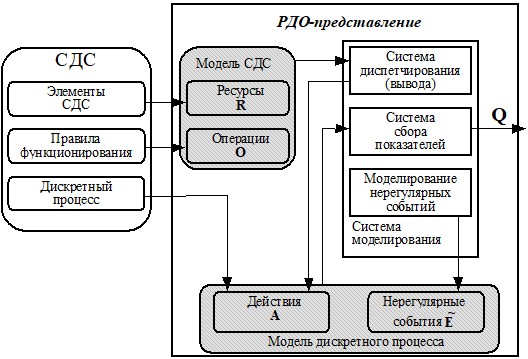
Рис.5. Представление СДС в РДО-методе
Ресурсы могут быть разбиты на несколько типов; каждый ресурс определенного типа описывается одними и теми же параметрами.
В среде РДО можно моделировать информационные потоки с различными законами распределения (равномерным, нормальным, экспоненциальным и т. п.). Обобщенно процесс анализа системы посредством вычислительной модели показан на рис.6.
Процесс моделирования начинается с определения структуры системы, на основе которого устанавливаются границы составляющих модели и необходимый уровень детализации моделируемых процессов. Обосновывается выбор зависимых и независимых переменных, определяется тип модели (стохастическая, детерминированная и др.). Исходные данные определяются на основе эмпирических данных, идентификации и спецификации определяемых переменных. Что касается рассматриваемого технологического процесса — термической обработки цементного клинкера, то для формирования исходных данных необходимо учитывать сложность объекта: процесс обжига клинкера в печи подвержен влиянию множества разнородных факторов. Главные из них — количество, химический состав шлама, расход, температура, калорийность топлива, расход и температура вторичного воздуха и множество других.
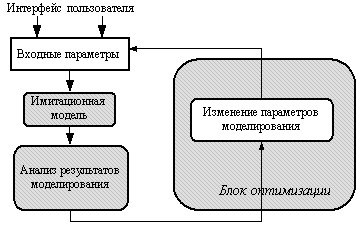
Рис.6. Обобщенное представление процесса моделирования
Исходные данные и начальные условия, уровень детализации которых на начальном этапе определяется оператором, могут быть представлены, например, в виде некоторой матрицы, строки которой соответствуют определенной операции процесса, а столбцы как раз и являются характеристиками операции. Успешность моделирования зависит от того, насколько хорошо оператор умеет выделять существенные элементы и взаимосвязи между ними.
Исходя из специфики технологического процесса, могут быть сформулированы следующие ограничения на:
- количество операций, заданных технологией; последовательность выполнения операций; расход шлама; производительность печи (по техническому паспорту печи); удельный расход условного топлива; влажность шлама, температура вторичного воздуха; скорость вращения печи (не более 1 об/мин).
Частота поступления шлама в печь может быть определена, например, законом распределения, устанавливающим длительность интервалов между входными сигналами предыдущей операции.
Перечисленные ограничения представляются общими для любого варианта исходных данных.
В четвертой главе решаются задачи разработки имитационной модели и проведения имитационных экспериментов.
Исходным этапом моделирования представляется определение ресурсов модели, в данном случае — элементов вращающейся печи, которые непосредственно связаны с процессами обжига и охлаждения клинкера. В качестве таковых выступают определенные параметра агрегата, технологические зоны печи, устройства контроля и управления, так что для конкретной задачи могут быть предложены различные варианты моделей. Наиболее рациональным решением представляется рассмотрение печи в целом — агрегата для получения клинкера — как единого ресурса, поскольку именно в этой модели возможно размещение и хранение практически всей информации об его функционировании.
С целью последовательного улучшения технологического режима вращающегося печи и снижения удельного расхода топлива целесообразно обеспечить следующие условия:
- Нормализация работы шламопитателя. Снижение удельного расхода топлива на обжиг клинкера. Увеличение часовой производительности печи.
Имитационное моделирование представляет собой процесс построения обобщенной компьютерной модели с алгоритмическим описанием основных правил ее поведения.
В методе РДО знания о моделируемой системе представляются в виде модифицированных продукционных правил. Состояние любого моделируемого объекта системы определяется набором значений параметров всех элементов, принадлежащих системе и соответствующей базе данных (БД).
Пусть характеристики системы Zi(t) будут случайными функциями времени, зависящими от параметров ф1, ф2, …, фn. Разобьем эти параметры на две группы: управления — ф1, ф2, …, фm, определяющие дальнейший порядок функционирования системы, и собственные — фm+1, ф m+2, …, фn, характеризующие свойства системы и ее элементов и не зависящие от управления. Пусть некоторое свойство системы описывается функционалом Ф, взятым в качестве показателя и определенным в пространстве Zi(t):
Ф = Ф(ф1, ф2, …, фm; фm+1, ф m+2, …, фn). (23)
На величины фi накладываются ограничения вида:
лi(ф1, ф2, …, фm; фm+1, ф m+2, …, фn), (24)
h = 1, 2, …, h*, 0 ≤ фj ≤ бi. (25)
Можно утверждать, что задача оптимального управления сведется к выбору параметров фm+1, ф m+2, …, фn, удовлетворяющих условиям (24) и обеспечивающих минимум функционала Ф (23).
Если Ф = Ф(ф1, ф2, …, фn) и лh(ф1, ф 2, …, фn), заданные моделирующим алгоритмом, является выпуклыми и непрерывно дифференцируемыми функциями n переменных, то задача выбора оптимального управления асимптотически эквивалентна задаче нахождения минимума функции
![]() (26)
(26)
при условиях 0 ≤ фj ≤ бi (c > 0 — некоторое постоянное число). Под асимптотической эквивалентностью мы будем понимать эквивалентность при c → ∞. Таким образом, в результате замены (23) эквивалентным соотношением (26) мы пришли к задаче, которая может быть решена любым из известных методов отыскания экстремума.
Суть его сводится к следующему. Пусть искомыми величинами будут ф1, ф2,.., фw. Тогда в W-мерном пространстве выбираем произвольную точку б1, б2, …, бn, которую будем называть точкой нулевого приближения, а значение V(ф1, ф2, …, фw) обозначим V0. Отправляясь от этой точки, используем итерационную процедуру покомпонентной минимизации величины V как функции одной переменной. Минимизация функции V по каждой переменной может быть проведена различными способами. Рассмотрим алгоритм минимизации функции:
![]() ,
,
приняв во внимание физическую особенность функционирования технологической операции:
при ![]() и
и ![]() .
.
Пусть минимум функции находится в интервале (0, ф), то есть, правая граница интервала неизвестна. Произвольно выбираем значение аргумента ф = ф1 и методом агрегативного моделирования определяем функционал F1 при этом аргументе, соответственно увеличиваем значение аргумента ф = ф2 = 2ф1. Значение функционала F2 варьируется аналогичным образом — до тех пор, пока не выполнится условие
Fn > F1 (n = 2, 3, 4, …).
Для определения левой границы интервала поступаем следующим образом. Интервал (0, ф) делим пополам (значение функции при аргументе ф/2 было определено при поиске правой границы). Вновь полученный интервал (ф/2, ф) снова делим пополам, и в этой точке также определяем значение функции. Рассмотрим два случая взаимного соответствия этих значений.
Случай 1-й (рис.7,а). Если соблюдается условие FA>FB<FN, то минимум функции находятся в интервале (a, n). Для определения минимума функции отрезки a, b и b, n делим пополам, получая, соответственно, точки c и d, и вычисляем при этих аргументах значения функции (точки C, D), и далее — с заданной степенью точности определяем минимальное значение функции методом пяти точек.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




