Федеральное агентство по образованию
Государственное образовательное
Учреждение высшего профессионального образования
«Омский государственный технический университет»
, ,
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Конспект лекций
Омск 2005
УДК
ББК 22.21 я 73
Г79
Рецензенты:
, д-р техн. наук, профессор СибАДи
, д-р техн. наук, профессор ОмГУПС.
, ,
Г79 Теоретическая механика: Конспект лекций. – Омск: Изд-во ОмГТУ, 2005. – 61 с.
В конспекте лекций по курсу «Теоретическая механика» рассмотрены основные положения: теоремы, правила, формулы, алгоритмы расчета. Они проиллюстрированы примерами решения задач.
Конспект лекций предназначен для дистанционного обучения студентов очной и заочной форм обучения всех специальностей.
© , , 2005
© Омский государственный
технический университет, 2005
Общий курс теоретической механики состоит из трех разделов: статика, кинематика и динамика. В первой части рассматриваются основные теоремы и положения, а также приведены формулы для решения наиболее распространенных типов задач статики, кинематики и динамики. При этом не рассматривается подробно вывод формул или доказательства применяемых правил, т. к. это подробно освещено в учебной литературе по теоретической механике.
СТАТИКА
Статикой называют раздел теоретической механики, в котором изучают способы преобразования системы сил, приложенных к твердому телу, в эквивалентные, а также условия равновесия сил приложенных к телу. Из данного определения видно, что основным понятием при изучении статики, является понятие силы. В статике под силой понимается мера механического взаимодействия материальных тел. Сила является величиной векторной, т. е. определяется следующими тремя факторами:
– точкой приложения силы;
– направлением силы;
– численным значением силы.
Следует отметить, что сила является вектором скользящим, т. е. точка её приложения может быть расположена в любом месте на линии её действия. Так как сила является векторной величиной, то при их сложении пользуются соответствующими правилами сложения векторов.
Введем следующие основные определения для сил. Совокупность нескольких сил, действующих на тело, будем называть системой сил. Системы сил, под действием каждой из которых тело находится в одинаковом кинематическом состоянии, называются эквивалентными. Сила, эквивалентная некоторой системе сил, называется равнодействующей. Сила равная по модулю равнодействующей и направленная по линии её действия, но в противоположную сторону, называется уравновешивающей. Система сил, которая, будучи приложенной, к телу, находящемуся в покое, не выводит его из этого состояния, называется системой взаимно уравновешенных сил.
Силы, действующие на механическую систему делятся на внешние и внутренние. Внешними называются силы, действующие на точки и тела со стороны точек или тел, не принадлежащих этой системе. Внутренними будем называть силы, взаимодействия между точками, принадлежащими данной системе.
Связи и реакции связей
Тело считается свободным, если его перемещения ничем не ограничены. Если же перемещения тела ограничены другими телами, то его называют несвободным, а тела ограничивающие перемещения данного тела называются связями. Сила, с которой тело, осуществляющее связь, действует на данное рассматриваемое тело, препятствуя его перемещению в том или ином направлении, называется реакцией этой связи. Направление реакции связи противоположно тому направлению, по которому связь препятствует двигаться данному телу.
В зависимости от характера закрепления тела, или от вида опоры можно указать следующие виды связей и направления их реакций:
1. Тело опирается на неподвижную поверхность в точке (рис. 1).
2. Тело опирается в трех точках по схеме (рис. 2).
3. Связь осуществляется при помощи гибких нитей, тросов. Реакции таких связей направлены по направлению нитей (рис. 3).
4. Связи, используемые для балочных конструкций (рис. 4).
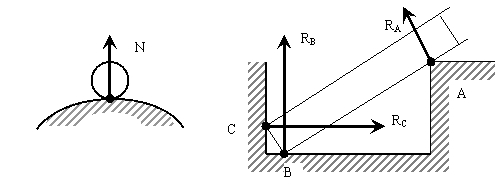

Рис. 1 Рис. 2
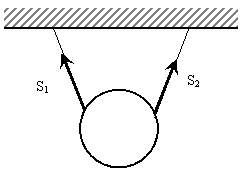
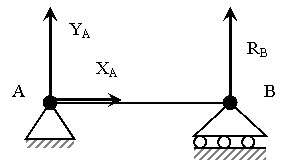
Рис. 3 Рис. 4
Опора А называется шарнирно-неподвижной и имеет две составляющие опорной реакции, опора В называется шарнирно подвижной и имеет одну составляющую, направленную перпендикулярно опорной поверхности.
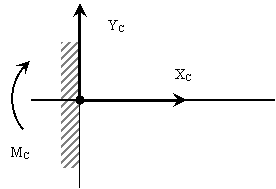 5. Связь, называемая жесткой заделкой (рис. 5) имеет три составляющих опорной реакции.
5. Связь, называемая жесткой заделкой (рис. 5) имеет три составляющих опорной реакции.
Одной из основных задач механики является определение опорных реакций. Для решения данной задачи используют принцип освобождаемости от связей: всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к данному телу. Данный принцип позволяет действительную модель нагружения заменить расчетной схемой.
Рис. 5
СИСТЕМА СХОДЯЩИХСЯ СИЛ
Сходящимися называются силы, если их линии действия пересекаются в одной точке. При решении задач на систему, сходящихся сил используются два способа: геометрический и аналитический. Геометрический метод основан на определении, что для уравновешенной системы сходящихся сил силовой многоугольник должен быть замкнутым.
В основу аналитического метода положено понятие проекции силы на ось. Проекцией силы на ось будем называть длину отрезка оси, заключенную между проекциями начала и конца данной силы на ось, взятую с соответствующим знаком (рис. 6).
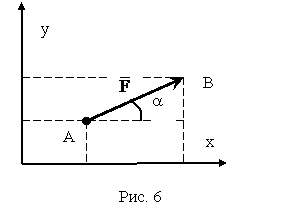 Из рис. 6 видно, что Fx = F∙ cos a,
Из рис. 6 видно, что Fx = F∙ cos a,
Fy = F∙sin a. Принимая во внимание, что для системы сходящихся сил, находящихся в равновесии, проекции равнодействующей на соответствующие координатные оси будут равны нулю, получаем аналитические условия равновесия системы:
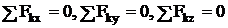 .
.
Задача 1
Однородная балка длины ![]() и веса Р удерживается в равновесии нитью ВС и шарниром А. Найти натяжение нити и реакцию шарнира А, если
и веса Р удерживается в равновесии нитью ВС и шарниром А. Найти натяжение нити и реакцию шарнира А, если ![]() (рис. 7). Реакция нити ВС направлена по нити, а реакция шарнира А определяется в соответствии с теоремой о трех силах: если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Заменив действие связей их реакциями, мы можем перейти от реальной схемы нагружения к расчетной (рис. 7, а). Учитывая, что сила Р приложена в середине балки и следовательно точка К (точка пересечения сил), делит отрезок ВС пополам, определим углы в полученной фигуре. Решение данной задачи может быть проведено двумя методами: геометрическим и аналитическим.
(рис. 7). Реакция нити ВС направлена по нити, а реакция шарнира А определяется в соответствии с теоремой о трех силах: если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Заменив действие связей их реакциями, мы можем перейти от реальной схемы нагружения к расчетной (рис. 7, а). Учитывая, что сила Р приложена в середине балки и следовательно точка К (точка пересечения сил), делит отрезок ВС пополам, определим углы в полученной фигуре. Решение данной задачи может быть проведено двумя методами: геометрическим и аналитическим.
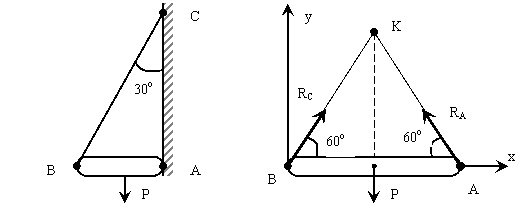

Рис. 7 Рис. 7, а
Геометрический метод.
Из сил, действующих на тело, строим силовой треугольник, который должен быть замкнутым, т. к. под действием этих сил тело находится в равновесии
(рис. 7, б). Для этого откладываем силы по известным направлениям, в любом выбранном масштабе.
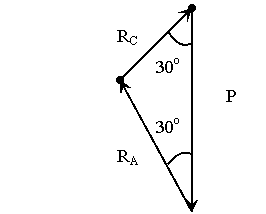 Таким образом, задача определения опорных реакций сводится к задаче решения полученного силового треугольника. Для решения воспользуемся теоремой синусов и составляем следующее соотношение:
Таким образом, задача определения опорных реакций сводится к задаче решения полученного силового треугольника. Для решения воспользуемся теоремой синусов и составляем следующее соотношение:
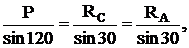
откуда получаем ![]()
Рис. 7, б
Аналитический метод.
Для решения задачи составляются уравнения равновесия в виде суммы проекций всех сил на оси координат. Направления осей показаны на рис.7, а.
![]() (1)
(1)
![]() (2)
(2)
Из первого уравнения получаем RC =RA. Из второго находим ![]() .
.
ПЛОСКАЯ СИСТЕМА СИЛ
Плоской называется такая система сил, линии действий которых расположены в одной плоскости. При рассмотрении плоской системы сил введем определения для нагрузок. Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на твердое тело
(рис. 8).
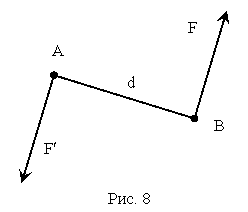 Плоскость, в которой расположена данная пара, называется плоскостью действия этой пары. Перпендикуляр, опущенный из точки приложения одной из сил на линию
Плоскость, в которой расположена данная пара, называется плоскостью действия этой пары. Перпендикуляр, опущенный из точки приложения одной из сил на линию
действия другой называется плечом пары (d). Действие пары сил определяется моментом пары. Численное значение момента пары определяется как произведение модуля одной из сил на плечо этой пары.
![]()
Приведем следующие два свойства пар сил:
1. Данную пару, не изменяя её действия на тело, можно переносить как угодно в плоскости её действия.
2. Не изменяя действия данной пары на тело, можно изменять модуль сил и плечо этой пары, сохраняя неизменным модуль и направление вращения пары.
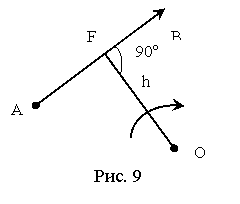 Другим важным понятием является момент силы относительно данной точки (рис. 9). Момент силы относительно данной точки равен произведению модуля силы на плечо, т. е. длину перпендикуляра, опущенного из этой точки на линию действия силы. Следовательно, будем иметь
Другим важным понятием является момент силы относительно данной точки (рис. 9). Момент силы относительно данной точки равен произведению модуля силы на плечо, т. е. длину перпендикуляра, опущенного из этой точки на линию действия силы. Следовательно, будем иметь
Mo(F)=±F∙h.
Момент силы считается положительным, если тело под действием данной силы стремится вращаться относительно точки О против часовой стрелки.
Отметим следующие свойства момента силы:
1. Момент силы относительно данной точки не изменяется при переносе точки приложения силы вдоль линии действия силы.
2. Момент силы относительно данной точки обращается в нуль в том случае, когда линия действия силы проходит через эту точку.
При решении задач на плоскую систему сил пользуются уравнениями равновесия. Для равновесия плоской системы сил необходимо и достаточно, чтобы сумма проекций этих сил на две координатные оси и сумма моментов относительно произвольно выбранной точки равнялись нулю
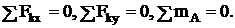
Существуют и две другие формы условий равновесия, но они используются гораздо реже.
Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось, не перпендикулярную к прямой АВ, были равны нулю.
Третья форма: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительной любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю.
 ;
;
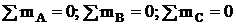 .
.
Задача 2
Лестница АВ длиной 2а и весом Р опирается на гладкий горизонтальный пол и 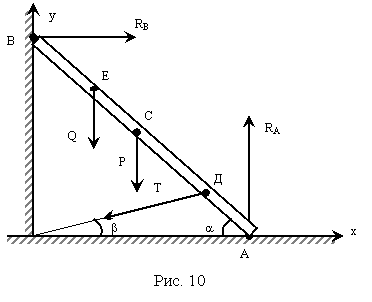 гладкую вертикальную стену, на которой в точке Е стоит человек весом Q. Чтобы лестница не скользила, она привязана к стене веревкой ОД. Определить реакции в точках А и В (стены и пола), а также натяжение веревки, если углы a и b, образуемые лестницей и веревкой с плоскостью пола известны и если расстояние
гладкую вертикальную стену, на которой в точке Е стоит человек весом Q. Чтобы лестница не скользила, она привязана к стене веревкой ОД. Определить реакции в точках А и В (стены и пола), а также натяжение веревки, если углы a и b, образуемые лестницей и веревкой с плоскостью пола известны и если расстояние 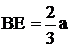 . Центр тяжести C лестницы находится в её середине (рис. 10).
. Центр тяжести C лестницы находится в её середине (рис. 10).
Решение: Используя принцип освобождаемости от связей, убираем связи, а их действие заменяем соответствующими реакциями. Составляем уравнения равновесия. Оси координат указаны на рис. 10.
![]() , (1)
, (1)
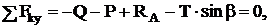 (2)
(2)
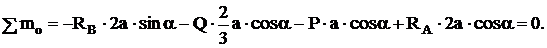 (3)
(3)
Из первого уравнения получаем: 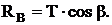
Из второго уравнения получаем: 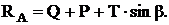
Подставляем значения для RA и RB в уравнение (3) и находим значение для
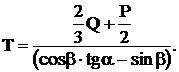
Задача 3
Определить опорные реакции в балочной конструкции, приведенной на
рис. 11, если Р=2 кН, q = 3 кН/м, m = 5 кНм. Размеры приведены на рис.11.
Решение: Используем принцип освобождаемости от связей, для чего вместо связей укажем их реакции (рис. 11, а). Указав оси координат для расчетной схемы, составляем уравнения равновесия. В данной задаче имеется три составляющих неизвестных опорных реакций, следовательно, необходимо составить три уравнения равновесия.
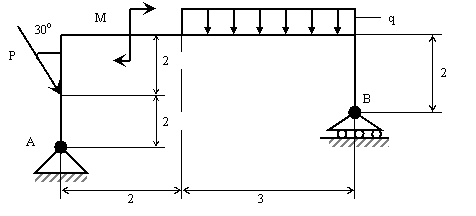

Рис. 11
Распределенная нагрузка, т. е. нагрузка приходящаяся на единицу длины, задается интенсивностью q= Н/см. Грузовая нагрузка, которая представляется как сосредоточенная сила равна Q=q∙ℓ, прикладывается в центре тяжести фигуры, образованной распределенной нагрузкой.
![]() , (1)
, (1)
![]() (2)
(2)
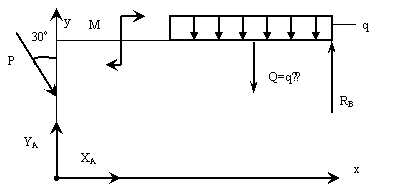

Рис. 11, а
При составлении третьего уравнения нужно учесть следующие два правила:
1. Момент от распределенной нагрузки равен, взятой с соответствующим знаком, площади грузовой нагрузки, умноженной на расстояние от центра тяжести грузовой нагрузки до рассматриваемой точки, относительно которой берется момент.
2. Если сила расположена под углом к координатным осям, то её необходимо разложить по проекциям на эти оси, а затем определять момент от каждой проекции в отдельности
![]() (3)
(3)
Момент следует брать относительно той точки, в которой сходятся большее количество неизвестных опорных реакций. Из полученных уравнений определяем неизвестные опорные реакции в следующем порядке:
из уравнения (3): ![]()
из уравнения (1): ![]()
из уравнения (2): ![]()
Следует отметить, что если при решении задач опорная реакция получилась со знаком минус, то, следовательно, её направление первоначально было выбрано неверно и его следует сменить на противоположное.
Система связанных тел
Во многих инженерных задачах приходится рассматривать равновесие не только одного тела, но и равновесие некоторой конструкции состоящей из нескольких тел. В этом случае приходится рассматривать равновесие каждого тела в отдельности, учитывая при этом силы, которыми действуют друг на друга тела, входящие в рассматриваемую систему. Тела могут быть соединены между собой с помощью шарнира, соприкасаться друг с другом и взаимодействовать одно с другим, вызывая определение силы взаимодействия. Эти силы, согласно аксиоме равенства действия и противодействия, всегда равны по модулю и противоположны по направлению.
Силы, с которыми тела, входящие в данную систему, действуют друг на друга, называются внутренними силами этой системы. Все остальные силы, включая сюда и реакции опор, называются внешними силами системы.
Если система находится в покое, то силы, приложенные к каждому из твердых тел, входящих в данную систему, уравновешиваются и, следовательно, для каждого из этих тел можно составить уравнения равновесия. В эти условия равновесия, для каждого тела в отдельности, войдут не только внешние силы, но и внутренние. Если же мы составляем уравнения равновесия для системы в целом, то внутренние силы, представляющие уравновешенную систему сил, в данные уравнения не войдут. Так для схемы, приведенной на рис. 12, 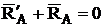 .
.
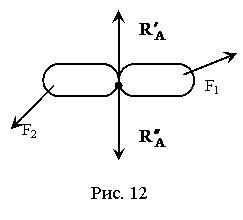 При рассмотрении равновесия сил, приложенных к системе тел, можно мысленно расчленить систему на отдельные твердые тела, добавляя при этом к внешним силам, силы взаимодействия между телами (внутренние силы) и составлять соответственно уравнения равновесия для каждого тела. Учитывая при этом, что для равнодействующей внутренних сил неизвестен не только модуль, но и направление, их обычно представляют в виде двух составляющих, направленных по двум осям координат. Таким образом, для системы, состоящей из N тел, когда на каждое тело действует плоская система сил, можно составлять 3N уравнений равновесия и, следовательно, определять 3N неизвестных.
При рассмотрении равновесия сил, приложенных к системе тел, можно мысленно расчленить систему на отдельные твердые тела, добавляя при этом к внешним силам, силы взаимодействия между телами (внутренние силы) и составлять соответственно уравнения равновесия для каждого тела. Учитывая при этом, что для равнодействующей внутренних сил неизвестен не только модуль, но и направление, их обычно представляют в виде двух составляющих, направленных по двум осям координат. Таким образом, для системы, состоящей из N тел, когда на каждое тело действует плоская система сил, можно составлять 3N уравнений равновесия и, следовательно, определять 3N неизвестных.
Задача 4
Составная балка состоит из двух участков АС и СД, соединенных в точке с шарниром (рис. 13). В точке А – неподвижная опора, в точке В – подвижная опора, конец Д балки поддерживается с помощью вертикальной тяги ДЕ. К балке СД приложена вертикальная сила F. Найти реакцию в шарнире ДЕ. Известно 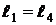 и
и 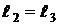 .
.
Решение: Используя принцип освобождаемости от связей, заменим действие связей соответствующими реакциями. Реакцию в шарнире А представим в виде двух составляющих XA и YA . Реакцию подвижной опоры обозначим RB , а реакцию нити – Т. В шарнире С разделим балку на два тела: стержень АС и стержень СД и для каждого участка в точке С обозначим равнодействующую внутренних сил в виде XC , YC и ![]() ,
, ![]() .
.
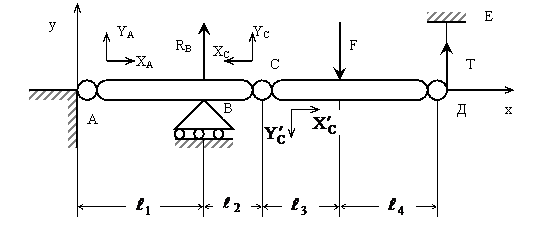

Рис. 13
Составим уравнения равновесия для участка АС
![]() (1)
(1)
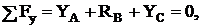 (2)
(2)
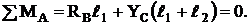 (3)
(3)
Уравнения равновесия для участка СД
![]() (4)
(4)
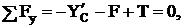 (5)
(5)
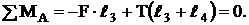 (6)
(6)
Учитывая равенства ![]() и
и ![]() получим:
получим:
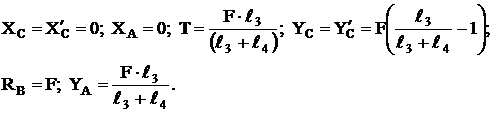
Задача 5
Для данной стержневой конструкции, представленной на рис. 14, определить величины опорных реакций.
Решение: Стержневая конструкция состоит из двух частей АС и ВС. Используя принцип освобождаемости от связей, заменим опоры их реакциями. Для жестко защемленной опоры А имеем три составляющих опорной реакции, для шарнирно подвижной опоры В – одну опорную реакцию. В точке разделения конструкции С имеем по две составляющих (для каждого участка) реакций внутренних связей, который будут попарно равны по модулю и противоположны по направлению.
Составим уравнения равновесия для участка АС.
![]() (1)
(1)
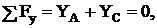 (2)
(2)
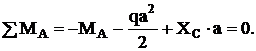 (3)
(3)
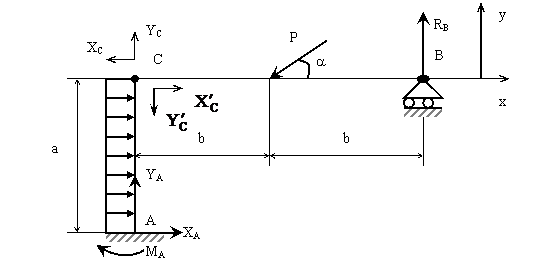

Рис. 14
Составим уравнения равновесия для участка ВС.
![]() (4)
(4)
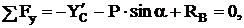 (5)
(5)
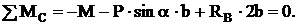 (6)
(6)
Из полученных шести уравнений, учитывая при этом равенства ![]() ,
, 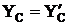 можно найти величины опорных реакций.
можно найти величины опорных реакций.
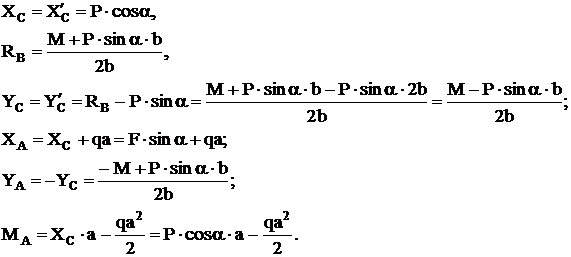
Произвольная система сил
Произвольной будем называть систему сил линии действия, которых расположены как угодно в пространстве. При изучении произвольной системы сил необходимо ознакомиться с понятием момента силы относительно оси.
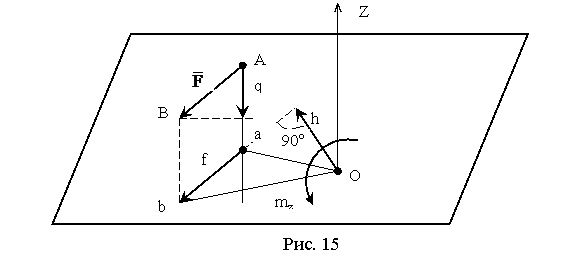
Пусть известна сила F, произвольно расположенная в пространстве. Разложим эту силу на две составляющие: одну параллельную оси Z, и другую f, лежащую на плоскости перпендикулярной оси Z. Опустим перпендикуляр на линию действия силы f и обозначим его h (рис. 15). Мерой вращательного эффекта, создаваемого силой f, будет служить момент силы относительно точки пересечения оси Z с плоскостью. Следовательно, величиной момента силы будет являться взятое с соответствующим знаком произведение mz = ±f∙h.
Из определения момента и из рис. 15 можно сделать следующие выводы:
1. Момент силы относительно оси равен нулю в том случае, когда линия действия силы пересекает ось или когда сила параллельна этой оси.
2. Момент силы относительно данной оси не изменяется при переносе точки приложения силы в любую другую точку на линии её действия.
 |
Уравнения равновесия, для произвольно расположенной в пространстве системы сил, получаются из условий, что главный вектор и главный момент равны нулю, т. е. ![]() и
и ![]() . Эти уравнения равновесия формулируются следующим образом: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций сил на каждую из трех координатных осей и суммы моментов относительно этих осей были равны нулю.
. Эти уравнения равновесия формулируются следующим образом: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций сил на каждую из трех координатных осей и суммы моментов относительно этих осей были равны нулю.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |




