При передаче вращения между телами с неподвижной осью (фрикционные без проскальзывания, зубчатые, цепные и ременные передачи) в точке контакта колес одинаковы значения VA и . Последнее позволяет, зная w и e ведущего звена 1, а также радиусы всех колес легко определить их угловые скорости и ускорения (рис. 9).

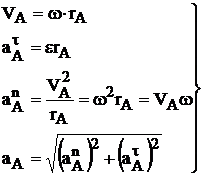(6)

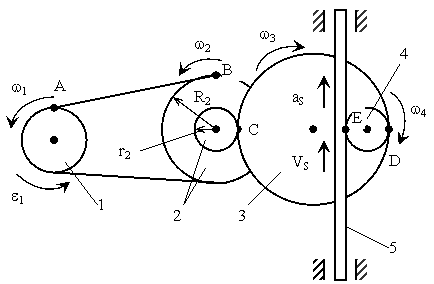
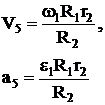
Рис. 9

Определение характеристик ведомого звена 5 осуществлялось переходом от одного звена к другому через общие точки A, B, C, D, E. При этом каждый раз угловая скорость (ускорение) ведущего звена умножалась на радиус вращения общей точки, а затем делилась на радиус вращения этой точки для ведомого колеса и т. д. При поступательном движении (участок ремня АВ и звено 5 скорости и ускорения точек одинаковы).

Плоскопараллельное движение

Движение тела называется плоскопараллельным или плоским, если тело перемещается так, что траектории всех его точек параллельны какой-то неподвижной плоскости. В качестве типичных примеров можно привести движение шатуна АВ в кривошипно-шатунном механизме или качение без проскальзывания колеса по плоскости или поверхности (рис. 10).

Для каждого момента времени и соответствующего ему положения кинематические характеристики движения произвольной точки звена, совершающего плоское движение, можно представить как векторную сумму двух характеристик: поступательного движения этой точки вместе с определенной точкой звена, выбранной за полюс и характеристиками поворота её вокруг полюса.

Обычно при решении задач, связанных с определением ускорений (скоростей), за полюс выбирают общую точку рассматриваемого звена и предыдущего, для которого движение задано или уже определено. Последнее позволяет сделать ускорение (скорость) полюса известным (на рисунках, представленных выше, за полюс выгодно взять точку А). В качестве точки, ускорение (скорость) которой необходимо найти, первоначально тоже выбирается общая точка рассматриваемого и последующего звена (точка В).

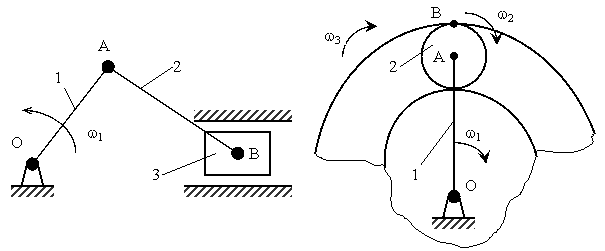Рис. 10

Последнее позволяет определить ускорение (скорость) этой точки хотя бы по направлению, что упрощает задачу. Таким образом, всегда можно получить векторные равенства

, (7)

где – характеристики искомой точки;

– характеристики для полюса;

– характеристики поворота вокруг полюса.

Далее необходимо сделать так, чтобы в уравнениях (7) осталось только два неизвестных, а затем спроецировать данное уравнение на удобно выбранные оси Х и Y и, решая полученную систему, определить их значения, т. е. решение уравнений (7) полностью аналогично аналитическому или графическому решению уравнений (5) для сложного движения точки.

Чтобы обеспечить в уравнениях (7) только два неизвестных (это всегда можно сделать), необходимо иметь в виду следующее: вектора 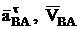всегда перпендикулярны радиусу АВ, а вектор направлен по радиусу к центру (полюсу) А и равен 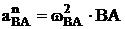. При этом, угловая скорость звена wВА, которая для выбранного положения звена не зависит от выбора полюса, может быть определена при решении уравнения для скоростей (7), т. к. , либо чаще через мгновенный центр скоростей (МЦС). МЦС это особая точка, скорость которой, в данном положении звена равна нулю. Находится он на пересечении перпендикуляров к скоростям двух точек звена, совершающего плоское движение.

Решить задачу с помощью МЦС можно, если известны скорость одной точки (например, А) по величине и направлению, а другой (например, В) по направлению (обычно это общие точки данного звена и смежных с ним звеньев). Это позволяет найти по величине, а также определить угловую скорость звена, например w2, совершающего плоское движение (рис. 11).

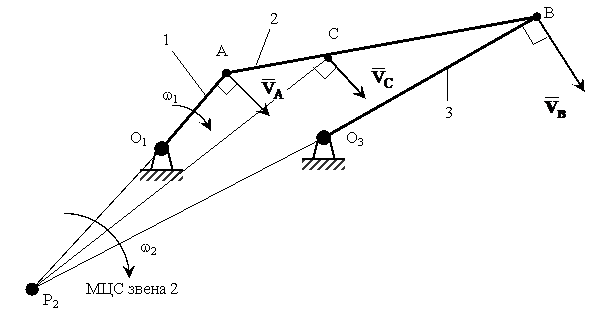
Рис. 11

Таким образом, если задано движение ведущего звена w1, размеры (длины звеньев , и ) и конкретное положение механизма (с помощью углов наклона звеньев с одной из осей), то можно найти и угловую скорость ведомого звена w3 для этого положения механизма. При этом учитывается, что точки А и В звена 2 общие со звеньями 1 и 3, совершающими вращение вокруг неподвижных осей, а значит эти скорости перпендикулярны радиусам О1А и О3В.

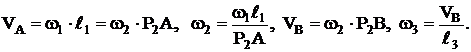(8)

Если необходимо найти скорость любой другой точки звена 2 (например, С), то её необходимо соединить с МЦС и её скорость будет перпендикулярна её радиусу, а равна VC=w2∙P2C.

Расстояния (радиусы поворота) от точек звена до МЦС определяются с помощью геометрии на основе заданных размеров и углов. Обычно они находятся в результате решения прямоугольных и остроугольных треугольников с использованием известных теорем синусов или косинусов.

В частном случае для положения механизма, когда перпендикуляры к скоростям точек А и В будут параллельны, МЦС стремится к бесконечности. Тогда и говорят, что звено 2 совершает мгновенно поступательное движение.

Рассмотрим другие частные случаи определения скоростей через МЦС, связанные с качением колес (последнее справедливо и для делительных окружностей зубчатых колес с движущимися центрами).

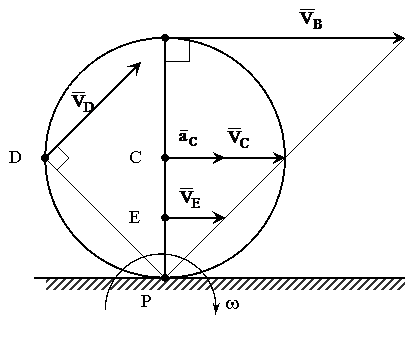Если колесо катится (без проскальзывания) по плоской или криволинейной неподвижной поверхности, то МЦС всегда будет в той точке колеса, которая касается этой поверхности (рис. 12).

Рис. 12

Если задано , радиус колеса R и другие необходимые расстояния и углы, то

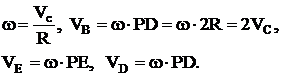(9)

Аналогично может быть определено и угловое ускорение колеса, если известно aC

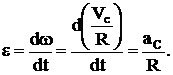(10)

Последнее справедливо, т. к. расстояние до МЦС центра колеса при движении не изменяется, т. е. не зависит от времени (для рычажных механизмов последняя формула не применяется).

Если поверхность, по которой обкатывается колесо, сама движется, то для определения положения МЦС колеса необходимо знать скорости двух точек колеса по величине и направлению (обычно это центр колеса С и точка касания движущейся поверхности, например точка В).

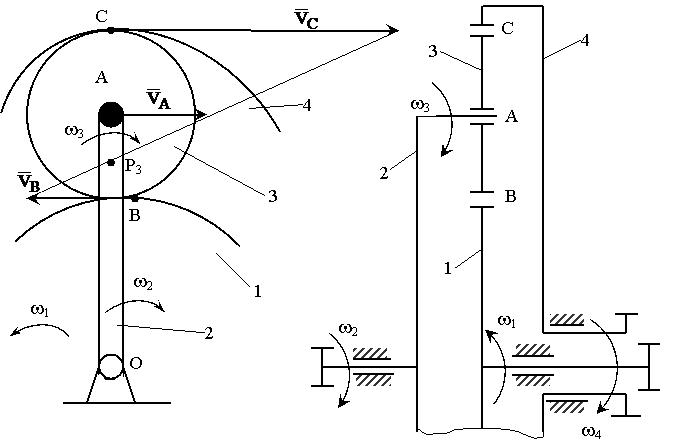
Рис. 13

На рис. 13 приведен пример дифференциального механизма, имеющего два ведущих звена (шестерня 1 и рычаг-водило 2), скорости которых w1 и w2 заданы. Промежуточным звеном является шестерня-сателит 3, совершающая плоское движение, а выходным – шестерня 4. Если заданы размеры механизма (радиусы или числа зубьев и модуль зацепления), то через МЦС колеса 3 можно определить движение ведомого звена w4 . Для точек А звена 2 и В звена 1, совершающих поворот вокруг неподвижного центра О справедливо VA=w2∙OA и VB=w2∙OB. Эти же точки принадлежат и звену 3, МЦС которого (точка Р3) может быть определен, если соединить концы векторов и . Положение этой точки на общем перпендикуляре к скоростям теперь находится из подобия треугольников, т. е.

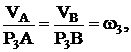(11)

где P3A=AB – P3B.

Решая последнюю систему уравнений легко определить

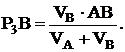(12)

Тогда можно найти w3 и далее скорость точки С этого же звена VC=w3∙P3C, а т. к. эта же точка принадлежит звену 4, вращающемуся вокруг неподвижного центра О, то для ведомого звена .

Если скорости точек А и В будут направлены в одну сторону (рис. 14), то МЦС может оказаться за пределами звена 3. В этом случае для определения его 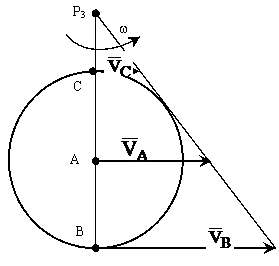тоже используются подобные треугольники и формула (11), в которой P3A=AB+P3B (рис. 14).

В частном случае, когда , получим w3 = 0 и скорости всех точек звена в этот момент одинаковы.

Если в данный момент времени известны касательные ускорения точек А и В, которые обычно находят через угловые ускорения ведущих звеньев 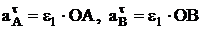или по заданному движению реек 1 и 2

(рис. 15), то аналогично w3 можно из подобия треугольников найти e3.

Рис. 14

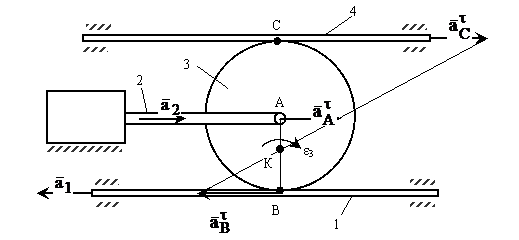
Рис. 15

Здесь

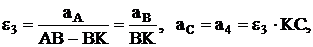
т. е. по заданному движению ведущих звеньев a1, a2 совершающих поступательное движение по прямой, получим aA = a1, aB = a2 и тогда, по выше приведенным формулам, легко найти e3 и ускорение ведомой зубчатой рейки a4.

В заключение рассмотрим на примере определения ускорений точек звеньев, совершающих плоское движение с использованием основной формулы (7) (рис. 16).

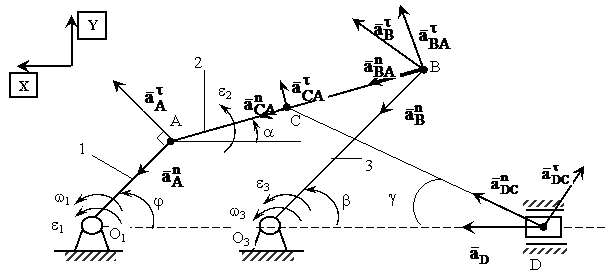
Рис. 16

Задача 3

Здесь должно быть задано или заранее определено: положение механизма в данный момент времени (углы j, a, b, g), кинематические характеристики ведущего звена (w1, e1), а также размеры звеньев и положение рассматриваемых точек . Это позволит найти ускорение всех точек звена 2, совершающего плоское движение, а также движение ведомых звеньев (w3, e3, aD). Для этого сначала определяется ускорение общей точки А и направление (прямые, по которым направлены вектора) ускорений другой общей точки В (учитывается их вращение вокруг неподвижных центров как на рис. 16, либо поступательное движение точки В вместе с ведомым звеном как на рис. 10). Тогда из выражения (7) следует

(13)

Величины нормальных ускорений вращения точки В вокруг центра О3 вместе со звеном 3 и – вращения этой точки вокруг полюса А вместе со звеном 2 найдем, используя значения w2 и w3, которые определяются через МЦС, как было рассмотрено выше в примере (см. рис. 11), т. е. 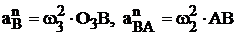. Тогда в векторном уравнении (13) остается две неизвестные и его можно спроецировать на оси Х и Y

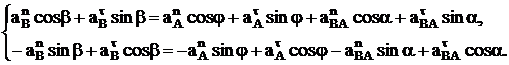(14)

Решая эту систему уравнений можно найти значения двух неизвестных 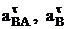, а затем 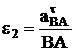и 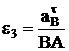. Если значение какого-то касательного ускорения окажется отрицательным, это означает, что правильное направление вектора противоположно первоначально выбранному на рис. 16 (соответственно противоположно направлено соответствующее угловое ускорение e2 или e3 ).

Зная w2 и e2 , теперь легко найти ускорение любой произвольной точки звена 2, например точки С. Для неё из уравнения (7) следует

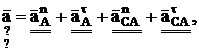(15)

где

Теперь проецируем (15) на оси

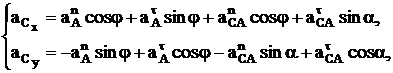(16)

и по проекциям находим модуль, а если необходимо, то и направление вектора .

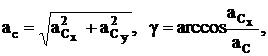(17)

где g – угол вектора с осью Х.

Если в точке С шарнирное соединение с другим звеном CD, совершающим плоскопараллельное движение, то точку С тоже можно взять за полюс и записать

. (18)

Последнее векторное уравнение решается аналогично уравнению (13).

Контрольные вопросы:

1. Чем отличаются координатный и естественный способ задания движения точки?

2. Что такое материальная точка?

3. Дать определение относительного, переносного и абсолютного движения точки.

4. Как определяется величина и направление кориолисова ускорения?

5. Определение поступательного движения тела и в чем особенности кинематики этого движения.

6. Как, зная уравнение вращения тела вокруг неподвижной оси, найти величину и направление его угловой скорости ускорения, а также линейную скорость и ускорение произвольной точки тела в любой момент времени?

7. Дать определение плоскопараллельного движения тела, и на какие два движения его можно разложить.

8. Как определить угловую скорость звена и линейные скорости его точек в плоскопараллельном движение через МЦС звена?

9. Как определяются ускорения точек звена, совершающего плоскопараллельное движение?

динамика

Динамикой называется раздел теоретической механики, в котором изучается движение тел в зависимости от действующих на них сил. Этот раздел является основным в курсе теоретической механики. Определение «теоретической» означает, что в основу разработки этого раздела положены некоторые теоретические предпосылки называемые аксиомами.

Динамика материальной точки

1. Аксиомы теоретической механики.

Во-первых, это три закона Ньютона:

– изолированная материальная точка движется равномерно и прямолинейно;

– ускорение, сообщаемое точке силой, пропорционально этой силе: ;

– тела взаимодействуют между собой с силами равными по величине и направленными в противоположные стороны по одной линии.

Во-вторых, это принцип независимости действия сил: ускорения, сообщаемые точке действующими на неё силами, независимы и могут быть сложены векторно:

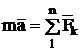. (1)

2. Дифференциальные уравнения движения материальной точки.

Спроектируем равенство (1) на декартовы оси:

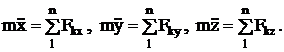(2)

Это и есть дифференциальные уравнения движения точки относительно декартовых осей координат, а если спроектировать равенство (1) на естественные оси координат:

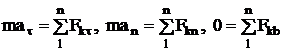
или

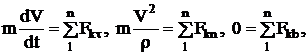(3)

то мы будем иметь дифференциальные уравнения движения точки в естественных координатах.

Динамика механической системы

Основные закономерности движения механической системы описываются общими теоремами динамики механической системы.

1. Механическая система. Силы внутренние и внешние.

Механической системой называется любая совокупность материальных точек, выделенная в данной задаче. Например, группа летящих самолётов вполне может рассматриваться как механическая система. Следует заметить, что и одна материальная точка, а также твёрдое тело могут считаться разновидностями механической системы.

Если между материальными точками существуют силы взаимодействия, то они называются внутренними и обозначаются .

Следует отметить, что геометрическая сумма (главный вектор) внутренних сил равна нулю ввиду того, что они действуют в механической системе попарно: как действие и противодействие.

Таким образом:

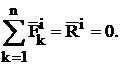
Главный момент системы внутренних сил также равен нулю в связи с тем, что внутренние силы действуют попарно по одной линии в разные стороны, следовательно, каждая пара имеет одно и то же плечо относительно любой точки. Моменты этих сил относительно любого центра будут равны по модулю, но будут иметь разные знаки.

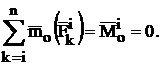
Внешними называются силы взаимодействия точек механической системы с телами или точками, не входящими в данную систему. Они обозначаются . Геометрическая сумма этих сил называется главным вектором внешних сил.

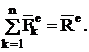
Механическая система, главный вектор внешних сил которой равен нулю, называется замкнутой.

Следует заметить, что понятие «главный вектор сил» является математической абстракцией, т. к. внешние и внутренние силы приложены к разным материальными точкам и реально сложены быть не могут.

2. Центр масс механической системы.

Центр масс механической системы это геометрическая точка, радиус–вектор которой определяется по формуле

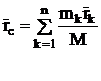. (7)

Представим эту формулу в более удобном виде:

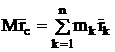(8)

или, проектируя на оси координат, запишем:

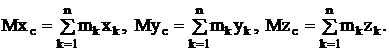(9)

Несомненным достоинством этого понятия является полная независимость от действия любых сил или систем сил. У твердого тела, находящегося в поле сил тяжести, центр масс совпадает с его центром тяжести.

3. Дифференциальные уравнения движения механической системы.

Основное уравнение движения отдельной материальной точки может быть записано в векторной форме:

(10)

а если она в составе механической системы, то, имея в виду деление сил на внешние и внутренние:

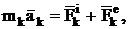(11)

где

Число таких уравнений равно числу точек системы, а в проекциях на оси координат

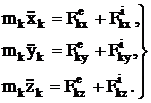(12)

Следует заметить, что внутренние силы входят в эти уравнения в весьма сложном виде. Они зависят друг от друга, от внешних сил, от координат и скоростей всех точек системы, поэтому аналитическое решение этих дифференциальных уравнений связано зачастую с непреодолимыми трудностями. Интегрирование этих уравнений численными методами с использованием ЭВМ хотя и расширяет круг решаемых задач, однако является более примитивным методом.

В то же самое время существует вполне определенный круг задач, где совершенно необязательно решать эти задачи в полном объёме относительно каждой точки. Кроме того, связи, наложенные на точки системы, позволяют сократить число неизвестных.

В механике разработаны методы, позволяющие обойти указанные трудности решения дифференциальных уравнений движения механической системы. Это дифференциальные уравнения движения механической системы в обобщенных параметрах, принципы механики и общие теоремы динамики системы: теорема о движении центра масс, теорема об изменении количества движения, теорема об изменении кинетического момента и теорема об изменении кинетической энергии.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4