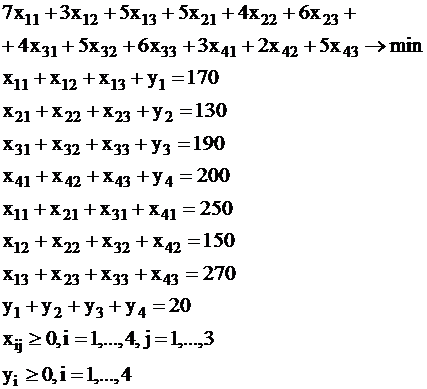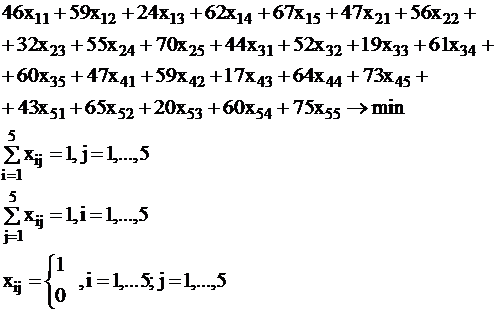Филина методы исследования в экономике: Методическое пособие (стр. 4 )

Решение:

В данной задаче количество руды, вырабатываемой в месяц четырьмя карьерами, на 20 тыс. т больше, чем мощностные возможности трех фабрик за тот же временной период. Сведем задачу к замкнутому виду, добавив фиктивного четвертого потребителя.

Модель рассматриваемой задачи выглядит так:

Заметим, что в целевую функцию не введены штрафы за нереализацию продукции в связи с их отсутствием в условии задачи.

Введем исходные данные в таблицу Microsoft Excel:

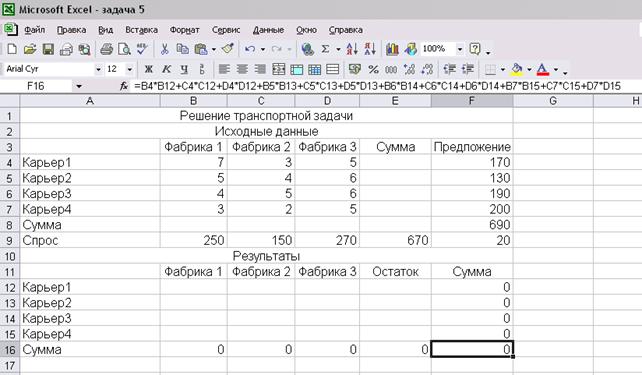
Рис. 23

Решим задачу при помощи модуля Поиск решения:

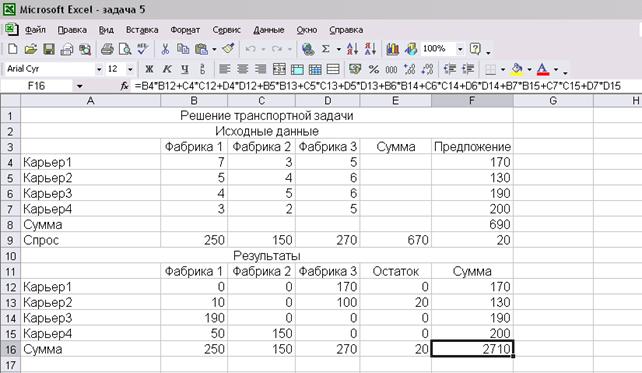
Рис. 24

Решим эту же задачу при помощи математической системы Mathcad:

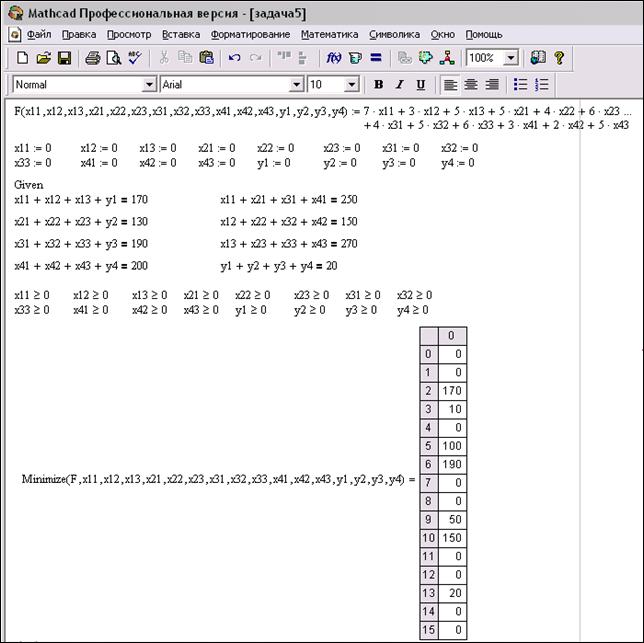
Рис. 25

Присвоив переменным полученные в ходе оптимизации значения, получим значение целевой функции равным 2710, что полностью совпадает с решением, полученным при помощи Microsoft Excel.

Это означает, что минимальные совокупные транспортные издержки в данной задаче равны 2710 тыс. руб. При этом значения переменных отражают количество руды (в тыс. т), перевозимое из карьера, определяемого первым индексом переменной, на фабрику, номер которой определяется вторым индексом.

Время, затрачиваемое на перегон состава из одного города в другой, указано в таблице (в часах).

Необходимо определить такой план доставки составов заказчикам, в соответствии с которым их перегон займет минимальное количество времени.

Задача 5.2

Четыре фермерских хозяйства, находящиеся в Рязанской, Владимирской, Тверской и Смоленской областях, направляют выращиваемые овощи и фрукты на переработку и консервацию на один из трех заводов, которые расположены в Москве, Туле и Ярославле.

Затраты на перевозку 1 т продукции представлены в таблице (в рублях):

В сезон Рязанское хозяйство производит 40 т продукции в неделю, Владимирское - 50 т, Тверское - 60 т, Смоленское - 70 т, в то время как завод в Москве может переработать в неделю 100 т продукции, в Туле - 50 т, в Ярославле - 40 т.

Составьте план перевозок продукции из фермерских хозяйств на заводы с минимальными транспортными расходами, учитывая, что в связи с ремонтом трассы Москва-Рязань в неделю по ней можно перевезти не более 20 т продукции.

Потребности фабрики А составляют 120 тыс. м3 в месяц, фабрики В - 140 тыс. м3, фабрики С - 110 тыс. м3, в то время как каждый из поставщиков вырабатывает в тот же период 75 тыс. м3 древесины.

Затраты на погрузку и разгрузку 1 тыс. м3 древесины составляют 30 руб.

Технические возможности не позволяют перевозить древесину от поставщика V на фабрику В.

Каковы минимальные затраты компании на выполнение условий контракта?

Задача 5.4

Маркетинговый отдел литейного завода прогнозирует спрос на производимые заводом детали в начале следующего года: январь - 10 тыс. шт., февраль - 14 тыс. шт., март - 16 тыс. шт., апрель - 12 тыс. шт.

При работе в одну смену можно изготавливать 12 тыс. деталей в месяц. Затраты на производство одной детали составляют 200 рублей. Если завод будет работать и во вторую смену, это позволит производить дополнительно 3 тыс. деталей в месяц, но затраты на производство одной детали во вторую смену составят уже 250 рублей.

Хранение детали на складе обходится заводу в 10 рублей в месяц.

Определите, сколько деталей нужно изготавливать каждый месяц, чтобы удовлетворить спрос с минимальными затратами.

Модель задачи в случае минимизации затрат о назначениях выглядит так:

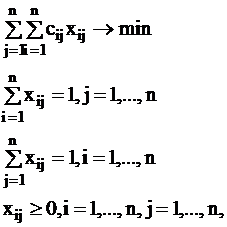(20)

где: сij - затраты на выполнение i-м рабочим j-й работы;

xij - переменная модели: xij=1, если i-й рабочий назначен на работу j, xij = 0, если i-й рабочий не назначен на работу j.

В случае максимизации эффективности использования рабочей силы за сij обозначают коэффициент, показывающий эффективность выполнения i-м рабочим j-й работы, и задача решается на максимизацию целевой функции.

Если количество рабочих не равно количеству работ, задача является открытой или несбалансированной и требует приведения к замкнутому виду путем введения недостающих рабочих или работ в необходимом количестве, для которых все сij = 0.

Пример:

Фирма получила заказ на разработку пяти программных продуктов.

Для выполнения заказа решено привлечь пятерых наиболее опытных программистов. Каждый из них должен написать одну программу. В таблице приведены оценки времени в днях, необходимого программистам для выполнения каждой из этих работ:

Как распределить работы между программистами, чтобы общее количество человеко-дней, затраченное на выполнение заказа, было минимальным?

Составим модель линейного программирования, отражающую условие:

Решим задачу при помощи Microsoft Excel:

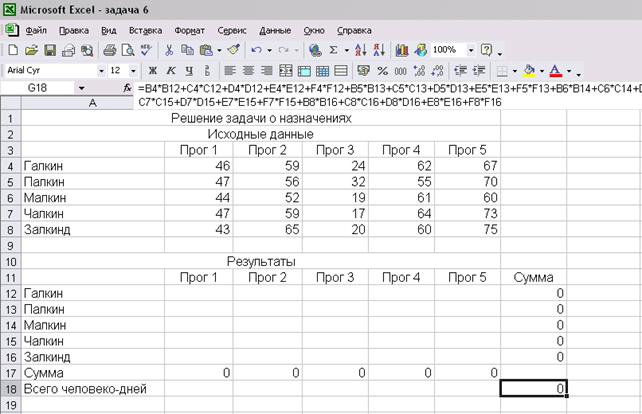
Рис. 26

При решении задач о назначении особый интерес вызывает способ ввода ограничений при заполнении формы модуля Поиск решения:

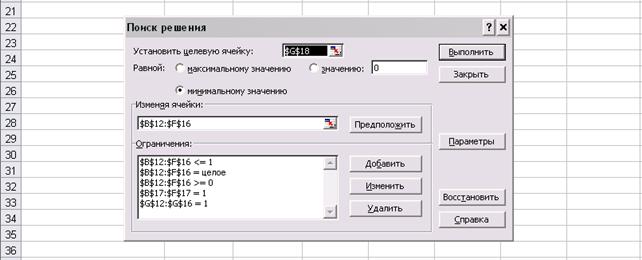
Рис. 27

Проведенные расчеты показывают, что минимальное количество человеко-дней для выполнения заказа составляет 234. Назначение программиста для создания программы определяется наличием на пересечении строки и столбца значения 1.

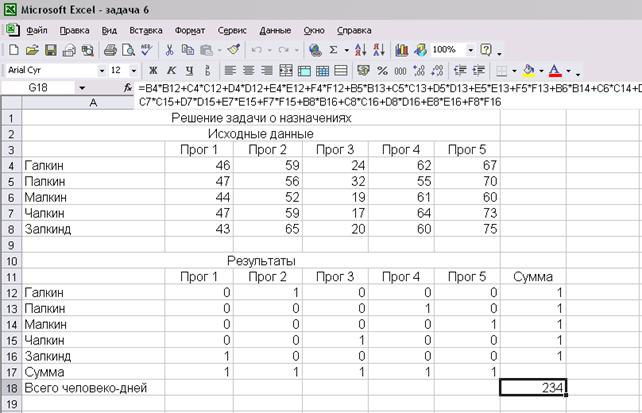
Рис. 28

Для решения задачи в Mathcad необходимо сначала задать целевую функцию, присвоить переменным их стартовые значения, а затем ввести ограничения, как показано на рис. 29.

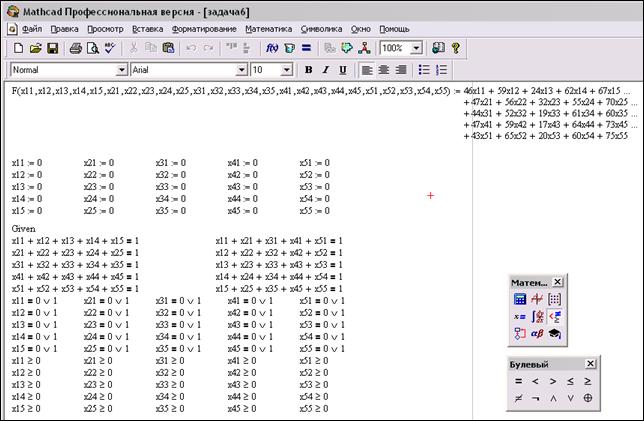
Рис. 29

Результатом вычислений с использованием функции minimize являются следующие значения переменных:

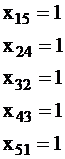
Значения остальных переменных равны нулю.

Полученное решение означает, что Галкину будет поручено выполнение работы 5, Палкину – работы 4, Малкину – работы 2, Чалкину – работы 3, Залкинду – работы 1.

Полученное решение не совпадает с решением этой задачи, полученным при помощи Microsoft Excel. Однако, присвоив переменным значения, полученные в процессе оптимизации, выясним, что значение целевой функции в данном случае равно 234. При решении задачи в Microsoft Excel значение целевой функции тоже равно 234. Это свидетельствует о наличии как минимум двух альтернативных решений задачи, при которых общее количество затраченных человеко-дней будет минимальным.

Задачи

Задача 6.1

В Центральном административном округе города Москвы открываются 4 магазина торговли по предварительным заказам - в районах Басманный, Замоскворечье, Мещанский и Таганский. Идея проекта состоит в том, что товары хранятся на четырех централизованных складах, находящихся в Северном, Северо-Восточном, Южном и Западном административных округах, и несколько раз в день по мере поступления заказов доставляются в магазины небольшими партиями.

Время, затрачиваемое на доставку продукции со складов в магазины, приведено в таблице (в минутах):

Руководство сети магазинов должно решить вопрос прикрепления магазинов к складам так, чтобы каждый склад обслуживал только один магазин, а время доставки товаров было минимальным.

Задача 6.2

Фирма получила заказ на срочный перевод четырех книг с итальянского языка. Фирма может располагать услугами 5 переводчиков, способных выполнить работу такого уровня. Время в днях, за которое каждый переводчик справится с работой, приведено в таблице:

Фирма использует повременную оплату труда. Переводчики имеют разную квалификацию, поэтому за день работы фирма платит Иванову 700 рублей в день, Петрову - 800 рублей в день, Сидорову - 600, Андрееву - 500, Васильеву - 550.

Поскольку по оценке фирмы качество переводов в итоге будет примерно одинаковым, руководство фирмы просит Вас составить такое распределение работ, которое позволит минимизировать затраты на переводы.

Задача 6.3

Компания "Евростройтур" организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию.

Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута):

Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.

Литература

1. , , Суворов задач по исследованию операций. - М.: Издательство Московского университета, 19с.

2. , Суворов операций в экономике: Учебное пособие. - М.: Экономический факультет МГУ, ТЕИС, 20с.

3. Excel, VBA, Internet в экономике и финансах. - СПб.: БХВ-Петербург, 20с.

4. , Попов методы. – М.: Форум – Инфра-М, 2005. – 464 с.

5. Салманов экономика с применением Mathcad и Excel. - СПб.: БХВ-Петербург, 20с.

6. , Нейман моделирование экономики. - М.: "Диалог-МИФИ", 20с.

7. Microsoft Office 2000 Шаг за шагом: Практическое пособие / Перевод с английского . – М: Издательство ЭКОМ, 2000 – 792 с.

Для заметок

Для заметок

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4