Задача 3.3
На лесопилку поступают доски длиной 10 м. По контракту лесопилка должна поставить клиенту не менее 100 досок длиной 5 м, не менее 200 досок длиной 4 м и не менее 300 досок длиной 3 м. Как работникам лесопилки выполнить условия контракта, разрезав наименьшее количество досок?
Задача 3.4
В цех поступила партия стержней длиной 110 и 80 см. Для дальнейшего производства требуется 50 стержней длиной 25 см и 50 стержней длиной 35 см. Как разрезать имеющиеся стержни, чтобы сократить отходы до минимума?
Оптимальное планирование финансов
Общая постановка задачи: определить виды вкладов, которые стоит использовать с целью минимизации размера целевого фонда или с целью получения максимального дохода.
Модель для решения задачи минимизации размера целевого фонда:
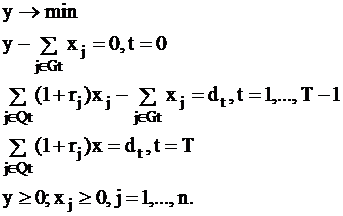 (13)
(13)
Модель для решения задачи максимизации дохода:
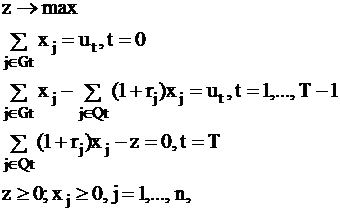 (14)
(14)
где: y - размер целевого вклада, создаваемого в момент времени 0;
t - текущий момент времени, t = 0,…,T;
dt - размер выплаты по займу, которую надо произвести в момент времени t = 1,…,T;
j - индекс срочного вклада, j = 1,…,n;
vj - момент времени вложения по срочному вкладу j;
wj - срок выплаты по срочному вкладу j;
rj - процент по вкладу j;
xj - объем вложений по срочному вкладу j;
Gt - множество индексов j, когда по вкладу j сделано вложение в момент времени t;
Qt - множество индексов j, когда по вкладу j получена выплата в момент времени t;
z - размер дохода, который может получить вкладчик в момент времени T;
ut - размер вклада в момент времени t, t = 0,…,T-1.
Пример решения задачи.
Компании необходимо выплатить поставщику оборудования 750 тыс. рублей. Из них 150 тыс. нужно выплатить через 2 месяца, а остальные 600 тыс. - через 6 месяцев после установки. Компанией принято решение образовать целевой фонд для получения дополнительных средств к моменту выплаты. Существующие возможные способы вложения денег представлены в таблице:
Тип вклада | Срок вклада (мес.) | Процент по вкладу |
A | 1 | 1,5 |
B | 2 | 3,5 |
C | 3 | 6,0 |
D | 6 | 11,0 |
Необходимо минимизировать размер целевого фонда.
Решение:
Составим таблицу, отражающую возможности вложения и возврата денег по месяцам:
Начало месяца | |||||||
Вклады | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
A1 | 1®® | 1,015 | |||||
A2 | 1®® | 1,015 | |||||
A3 | 1® | 1,015 | |||||
A4 | 1®® | 1,015 | |||||
A5 | 1®® | 1,015 | |||||
A6 | 1®® | 1,015 | |||||
B1 | 1®® | ®®® | 1,035 | ||||
B3 | 1®® | ®®® | 1,035 | ||||
B5 | 1®® | ®®® | 1,035 | ||||
C1 | 1®® | ®®® | ®®® | 1,06 | |||
C4 | 1®® | ®®® | ®®® | 0,06 | |||
D1 | 1®® | ®®® | ®®® | ®®® | ®®® | ®®® | 1,11 |
где: Ai - размер вклада типа A в месяце i;
Bi - размер вклада типа B в месяце i;
Ci - размер вклада типа C в месяце i;
Di - размер вклада типа D в месяце i.
Задача может быть описана следующей моделью:
| (15) |
Таблица исходных данных и форма Поиск решения в Microsoft Excel:
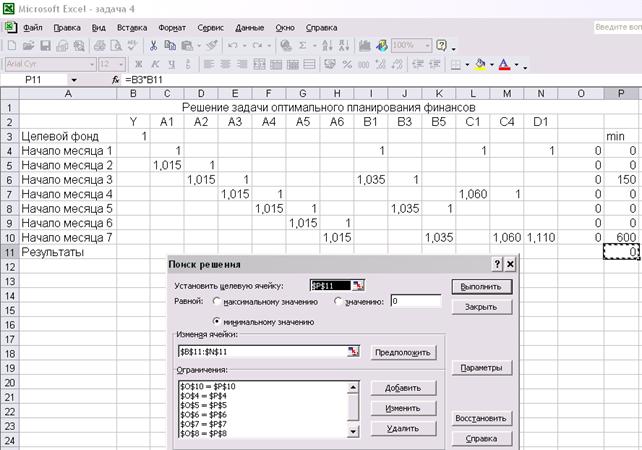
Рис. 20
Решение задачи в Microsoft Excel выглядит так:
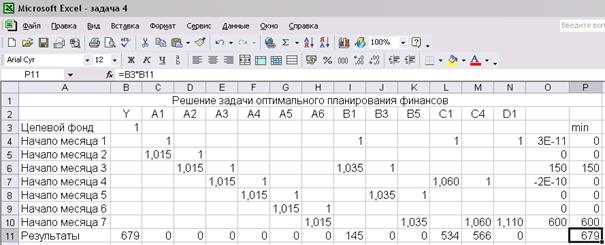
Рис. 21
Итак, минимальный размер целевого фонда, позволяющий сделать необходимые выплаты, составляет 679 тыс. руб. Для получения такого результата нужно использовать типы вкладов В и С.
Такой же результат можно получить и с помощью программы Mathcad:
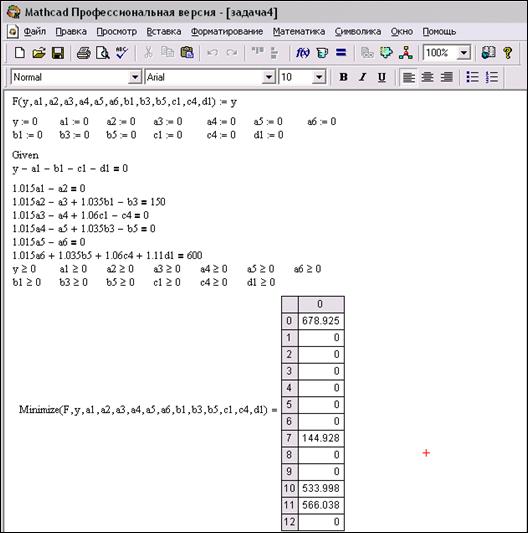
Рис. 22
Функция minimize возвращает вектор значений переменных, являющихся аргументами целевой функции, при которых ее значение будет минимальным. В первой колонке – порядковый номер переменной, начиная с нулевого, по очередности упоминания. Во второй – соответствующие значения переменных.
При необходимости, присвоив переменным полученные значения, можно рассчитать и значение целевой функции.
Задачи
Задача 4.1
Предпринимателю требуется для закупки товара 10000 рублей через 3 месяца. Сберегательный банк предлагает предпринимателю внести определенную сумму денег по одному из типов вкладов: А (сроком на 1 месяц под 2%) или В (сроком на 3 месяца под 6%). Необходимо определить тип вклада, который позволит получить требуемые средства в течение трех месяцев, вложив минимальную сумму денег.
Задача 4.2
Бендер хочет приобрести некий мебельный гарнитур, стоимость которого 100 тыс. рублей. Администрация аукциона согласна на выплату в рассрочку, с условием, что 20 тыс. руб. О. Бендер выплатит через 2 месяца, а остальную сумму - через 4 месяца.
Бендер, справедливо полагая, что найти требуемую сумму ему не удастся, хочет получить средства путем вложения денег по одному из типов вклада: А (сроком на 1 месяц под 1,5%), В (сроком на 2 месяца под 3,5%) или С (сроком на 4 месяца под 8%).
Какую сумму и по какому типу вклада нужно вложить О. Бендеру, чтобы через 4 месяца купить гарнитур?
Задача 4.3
Уезжая в длительную заграничную командировку, некий бизнесмен решил вложить в банк имеющуюся у него наличность в размере 50 тысяч рублей, воспользовавшись одним из способов:
Тип вклада | Срок вклада (мес.) | Процент по вкладу |
A | 1 | 1,5% |
B | 2 | 3,5% |
C | 4 | 8,0% |
Какую максимальную сумму денег сможет получить бизнесмен, вернувшись в Россию через 4 месяца?
Задача 4.4
Студент Иванов 31 мая получил стипендию, равную 5000 рублей. Воспользоваться полученными деньгами студент планирует не ранее 1 сентября. У студента имеется возможность инвестировать полученные средства по одному из вариантов:
Тип вклада | Срок вклада (мес.) | Процент по вкладу |
A | 1 | 2% |
B | 3 | 6% |
Каким способом инвестирования стоит воспользоваться, чтобы получить 1 сентября максимальное количество наличных средств?
Транспортная задача
Общая постановка задачи: определить маршруты доставки различных объемов продукции от производителей к потребителям, минимизируя затраты на их транспортировку.
Модель:
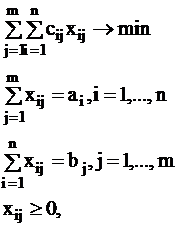 (16)
(16)
где: ai - величина предложения продукции в пункте i;
bj - величина спроса на продукцию в пункте j;
cij - затраты на транспортировку единицы продукции из пункта i в пункт j;
xij - количество продукции, перевозимое из пункта i в пункт j.
В случае, если 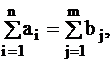 транспортная задача называется замкнутой или сбалансированной. В противном случае имеется либо перепроизводство продукции, когда
транспортная задача называется замкнутой или сбалансированной. В противном случае имеется либо перепроизводство продукции, когда  либо ее дефицит:
либо ее дефицит: 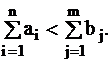
Задача с перепроизводством или дефицитом продукции должна быть обязательно сведена к замкнутому виду. При перепроизводстве вводят фиктивного m+1-го потребителя, причем 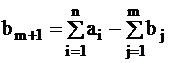 . Тогда замкнутая задача имеет вид:
. Тогда замкнутая задача имеет вид:
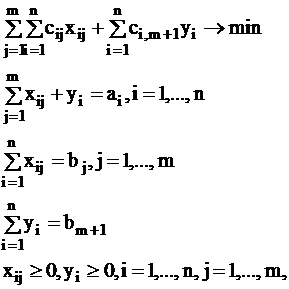 (17)
(17)
где: сi, m+1 - штраф за единицу нереализованной продукции в пункте i;
yi - количество продукции, нереализованное в пункте i.
В случае дефицита продукции действуют аналогично, вводя фиктивного n+1-го производителя, 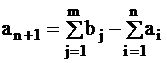 . Тогда замкнутая задача имеет вид:
. Тогда замкнутая задача имеет вид:
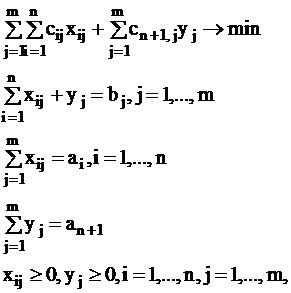 (18)
(18)
где: сn+1,j - штраф за единицу недопоставленной продукции в пункт j;
yj - количество продукции, недопоставленное в пункт j.
В условии транспортной задачи могут встречаться также дополнительные условия, например, запреты, ограничения на пропускные способности, фиксированные перевозки, введение новых мощностей и т. д.
Пример решения задачи:
Компания, занимающаяся добычей железной руды, имеет четыре карьера. Производительность карьеров составляет 170, 130, 190 и 200 тыс. т ежемесячно. Железная руда из карьеров направляется на три обогатительные фабрики, мощности которых составляют 250, 150 и 270 тыс. т в месяц. Транспортные затраты (в тыс. руб.) на перевозку 1 тыс. т руды с карьеров на фабрики указаны в таблице:
Фабрика 1 | Фабрика 2 | Фабрика 3 | |
Карьер 1 | 7 | 3 | 5 |
Карьер 2 | 5 | 4 | 6 |
Карьер 3 | 4 | 5 | 6 |
Карьер 4 | 3 | 2 | 5 |
Определите план перевозок железной руды на обогатительные фабрики, который обеспечивает минимальные совокупные транспортные издержки.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |





