Учебно-методический комплекс по дисциплине «Проектирование мостов» (стр. 4 )

2.2. Нормативные нагрузки

Главную балку рассчитывают на нагрузки, действующие в стадиях изготовления, хранения, транспортировки, монтажа и эксплуатации. В курсовом проекте разрешается не рассчитывать балку в стадиях транспортировки и монтажа. В стадии эксплуатации балку рассчитывают на постоянные нагрузки от собственного веса конструкции, от воздействия предварительного напряжения арматуры и на временную нагрузку от подвижного состава.

Нормативная постоянная нагрузка от собственного веса конструкций пролетного строения и веса тротуаров с перилами, приходящаяся на 1 м длины одной балки, кН/м (тс/м):

,

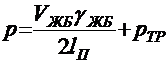где VЖБ ― объем железобетона пролетного строения, который для курсового проектирования можно принимать по прил. 1;

γЖБ = 24,5 кН/м3 (2,5 тс/м3) — объемный вес железобетона;

lП — полная длина пролетного строения, м;

рТР = 2,45 кН/м (0,25 тс/м) ― вес тротуаров с перилами.

Нормативная постоянная нагрузка от веса балласта с частями пути, приходящаяся на 1 м длины одной балки:

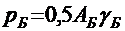, кН/м3 (тс/м3),

где АБ = 2 м2 — площадь сечения балластной призмы;

γБ = 19,4 кН/м3 (2 тс/м3) — нормативный объемный вес балласта с частями пути.

Нормативная временная вертикальная нагрузка от подвижного состава принимается в виде эквивалентной равномерно распределенной нагрузки интенсивностью ν , кН/м (тс/м), пути, значение которой определяют по прил. 4 в зависимости от класса К временной нагрузки, длины загружения ‚ и коэффициента α.

Для пролетных строений с ездой на балласте при длине загружения λ ≤ 25 м эквивалентную нагрузку определяют при α = 0,5 независимо от положения вершины линии влияния.

В стадии изготовления и хранения единственной нагрузкой

будет собственный вес конструкции без тротуаров и перил:

.

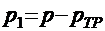2.3. Расчетные усилия

Для расчетов в стадии эксплуатации вычисляют следующие

усилия в сечениях главной балки.

Для сечения посередине пролета:

изгибающий момент для расчета по прочности

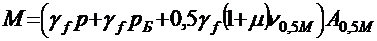; (2.1)

максимальный изгибающий момент для расчета на выносливость

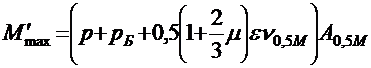; (2.2)

минимальный изгибающий момент для расчета на выносливость

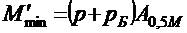; (2.3)

поперечная сила для расчета по прочности

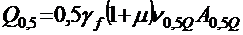; (2.4)

изгибающий момент для расчета по трещиностойкости в стадии эксплуатации

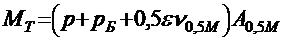; (2.5)

Для опорного сечения:

поперечная сила для расчета по прочности

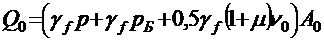; (2.6)

В приведенных формулах:

γf ― коэффициент надежности по нагрузкам (прил. 5, табл. 5.1);

ε ― коэффициент, учитывающий отсутствие тяжелых транспортеров (прил. 5, табл. 5.2);

1+μ и 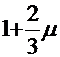― динамические коэффициенты для расчета, соответственно, по прочности и на выносливость (прил. 5, п. 5.3, в).

В стадии изготовления и хранения определяют изгибающий момент для расчета по трещиностойкости:

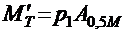; (2.7)

2.4. Подбор арматуры

Необходимую площадь рабочей арматуры в нижнем поясе балки определяют из условия прочности в стадии эксплуатации по следующей приближенной формуле:

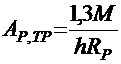; (2.8)

где М — изгибающий момент посередине пролета для расчета на прочность;

h — высота балки;

RP — расчетное сопротивление напрягаемой арматуры растяжению (прил. 8, табл. 8.1).

Нижний пояс балки армируют пучками из параллельных проволок или из арматурных канатов (см. табл. Б Задания) с натяжением арматуры на упоры. Необходимое количество проволок:

,

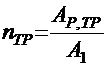где А1 ― площадь сечения одной проволоки.

В пучке проволоки размещают четырьмя прядями, в каждой из которых находится от 4 до 16 проволок или по одному арматурному (семипроволочному) канату К=7.

Принятое сечение пучка вычерчивают в масштабе 1:1 или 1:2 и определяют по чертежу его наибольший поперечный размер — диаметр dП (рис. 8, а). Количество пучков рабочей арматуры в нижнем поясе балки:

,

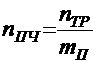где mП ― количество проволок в одном пучке.

При определении количества пучков и проволок в них рекомендуется ориентироваться на данные типовых проектов, помещенные в табл. 4. Пучки размещают горизонтальными рядами в нижнем поясе балки (рис. 8, б). Между пучками должно быть расстояние в свету не менее диаметра пучка или 6 см, наименьшая толщина защитного слоя бетона для пучков равна 4 см. После размещения пучков уточняют размеры его пояса.

Расчетная площадь напрягаемой арматуры:

в нижнем поясе ;

в верхнем поясе ,

где nПЧ — число пучков в нижнем поясе;

— то же, в верхнем поясе (не менее двух);

АР1 — площадь сечения одного пучка.

Обычно .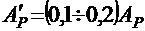

Расстояние от центра тяжести площади сечения напрягаемой арматуры в нижнем поясе до нижней грани балки:

,

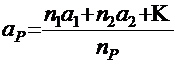где 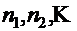— количество пучков, соответственно, в первом, втором и др. (считая снизу) горизонтальных рядах арматуры;

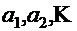— расстояния, соответственно, от оси каждого горизонтального ряда арматуры до нижней грани балки (см. рис. 8,б).

Расстояние от центра тяжести площади сечения напрягаемой арматуры в верхнем поясе до верхней грани балки:

,

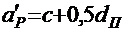где с = З см ― толщина защитного слоя бетона для плиты;

dП ― диаметр пучка.

2.5. Геометрические характеристики сечения

В курсовом проекте разрешается определять необходимые для последующих расчетов геометрические характеристики только одного сечения, расположенного посередине пролета балки. Помещенные ниже формулы относятся к балке с натяжением арматуры на упоры. При этом учтена только предварительно напряженная арматура.

Вычерчивают принятое сечение балки в масштабе 1:20 — 1:25 (рис. 9, а). Сложную форму сечения заменяют более простой двутавровой с прямоугольными полками (поясами) эквивалентной

площади. Ширину верхней полки принимают равной расстоянию между внешними гранями наружного и внутреннего бортиков.

Средняя высота верхней полки:

,

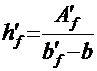где — площадь сечения наружного и внутреннего свесов верхней полки с учетом вутов (заштрихованная площадь на рис. 9, а), но без учета площадей бортиков;

b — толщина стенки балки.

Средняя высота нижнего пояса:

,

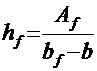где Аf ― площадь сечения нижнего пояса без учета стенки (заштрихованная площадь на рис. 5, а);

bf — ширина нижнего пояса балки.

Площадь приведенного сечения балки

.

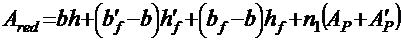Статический момент приведенного сечения относительно оси,

проходящей через нижнюю грань сечения:

.

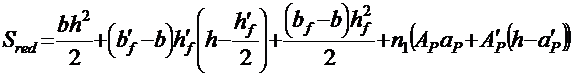Расстояние от центра тяжести площади приведенного сечения:

до нижней грани сечения ;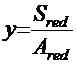

до верхней грани сечения ;

до центра тяжести нижней арматуры ;

до центра тяжести верхней арматуры .

Момент инерции приведенного сечения относительно оси, проходящей через центр тяжести:

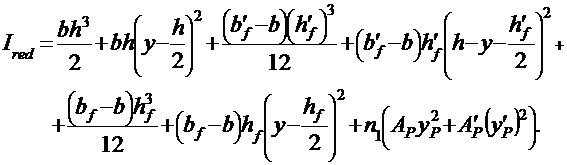
В этих формулах n1 — отношение модулей упругости арматуры к бетону EP/Eb , определяемых по примечанию 1 к табл. 9.3, прил. 9. Остальные обозначения — геометрические размеры, приведенные выше и на рис. 9, а.

2.6. Предварительные напряжения в бетоне и арматуре

Предварительное установившееся напряжение в нижней арматуре в стадии эксплуатации, минимально необходимое для удовлетворения категории 2а требований СНиП 2.05.03-84* по трещиностойкости балки:

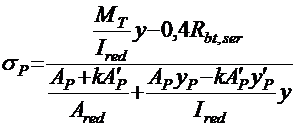; (2.9)

то же, в верхней арматуре: .

Равнодействующая усилий в напрягаемой арматуре в стадии

эксплуатации:

.

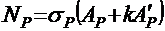Момент этой равнодействующей относительно центра тяжести приведенного сечения (рис. 9, б):

.

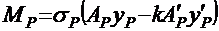Установившиеся предварительные напряжения в бетоне (рис. 9, в):

нижней грани балки

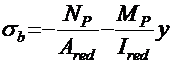; (2.10)

верхней грани балки

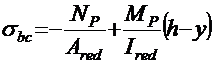. (2.11)

В приведенных формулах:

МТ ― изгибающий момент посередине пролета балки для расчета по трещиностойкости в стадии эксплуатации;

Rbt,ser — расчетное сопротивление бетона растяжению при расчетах по предельным состояниям 2-й группы (прил. 8, табл. 8.1);

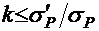— коэффициент, который в предварительных расчетах можно принимать равным 1.

Остальные обозначения — геометрические размеры, приведенные на рис. 9,а.

Потери предварительного напряжения арматуры учитывают от воздействия следующих факторов.

1. Релаксация напряжений арматуры:

,

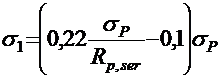где σР ― по формуле (2.9), МПа;

Rp,ser ― расчетное сопротивление арматуры растяжению при расчетах по предельным состояниям второй группы (прил. 9, табл. 9.1).

2. Температурный перепад при натяжении арматуры на упоры, МПа:

для бетона класса В40 и ниже σ2 = 1,25Δt;

для бетона класса В45 и выше σ2 = 1,0 ,

где Δt ― разность между температурой нагреваемой арматуры и неподвижных упоров, °С (при отсутствии точных данных следует принять Δt = 65°С).

3. Деформация анкеров, расположенных у натяжных устройств:

,

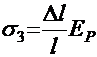где Δl — смятие и сжатие анкерных закреплений, принимаемое по 2 мм на каждый анкер;

l — длина натягиваемого арматурного элемента, мм;

ЕР — модуль упругости напрягаемой арматуры (прил. 9, табл.9,З).

4. Трение арматуры об огибающие приспособления (в курсовом проекте разрешается не учитывать, т. е. σ4 = 0).

5. Деформация стальной арматуры при изготовлении предварительно напряженных железобетонных конструкций σ5 = 30 МПа.

6. Быстронатекающая ползучесть для бетона (в курсовом проекте разрешается не учитывать, т. е. σ6 = 0).

7. Усадка бетона при натяжении на упоры с тепловой обработкой, МПа:

для бетона класса В35 и ниже σ7 = 35,

для бетона класса В40 σ7 = 40,

для бетона класса В45 и выше σ7 = 50.

8. Ползучесть бетона, МПа:

при ;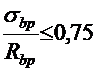

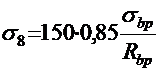при ,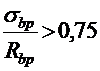

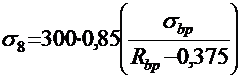где σbp― установившееся сжимающее напряжение в бетоне на уровне центра тяжести нижней напрягаемой арматуры,

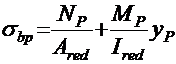; (2.12)

Rbp ― передаточная прочность бетона в момент передачи усилия обжатия на бетон, которую в курсовом проекте можно принять .

Контролируемые напряжения:

в нижней напрягаемой арматуре

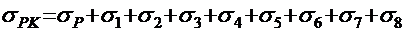; (2.13)

в верхней напрягаемой арматуре

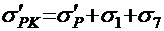. (2.14)

При этом должно соблюдаться условие ,

где RP ― расчетное сопротивление арматуры растяжению

m ― коэффициент условий работы, принимаемый равным:

m = 1,1 для арматурных элементов из высокопрочной проволоки;

m = 1,05 для арматурных канатов класса К-7.

Напряжения, передаваемые на бетон при создании предварительных напряжений:

в нижней напрягаемой арматуре

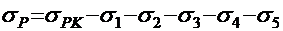; (2.15)

в верхней напрягаемой арматуре

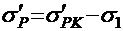. (2.16)

2.7. Расчет прочности по изгибающему моменту

Прочность балки в стадии эксплуатации проверяют по изгибающему моменту в сечении посередине пролета. В курсовом проекте допустимо не учитывать незначительное влияние ненапрягаемой арматуры (рис. 9, г).

Если соблюдается условие

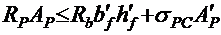, (2.17)

то граница сжатой зоны находится в верхнем поясе (полке), и расчет производится как для прямоугольного сечения с высотой сжатой зоны

.

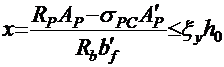Условие прочности:

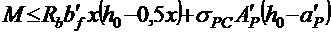. (2.18)

Если условие (2.17) не соблюдается, то граница сжатой зоны проходит в ребре.

Высота сжатой зоны:

.

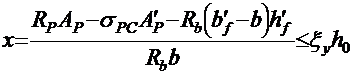Условие прочности:

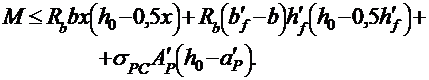(2.19)

В этих формулах:

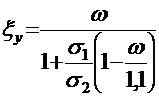― относительная высота сжатой зоны,

где ω = 0,85 – 0,008Rb (Rb в МПа);

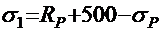, МПа ― напряжение в арматуре, где σР определяется по (2.9);

σ2 = 500 МПа ― предельное напряжение в арматуре сжатой зоны;

σРС ― расчетное напряжение в арматуре сжатой зоны, принимаемое не более 500 МПа (5100 кгс/см2).

Остальные обозначения приведены на рис. 9 и пояснены выше.

2.8. Места установки внутренних анкеров и изменения толщины стенки. Размещение хомутов.

Для определения мест установки внутренних анкеров в масштабе вычерчивают огибаю эпюру изгибающих моментов для половины балки (рис. 10, б). Изгибающий момент в сечении, расположенном на расстоянии 0,25 l от опоры, приближенно можно принять равным 0,75 М0,5.

На огибающей эпюре откладывают несущую способность балки Мнес — величину правой части формул (2.18) или (2.19), которую делят на число пучков в нижнем поясе балки. Через деления проводят горизонтальные прямые до пересечения с огибающей эпюрой моментов. Место теоретического обрыва пучка соответствует точке пересечения верхней границы полоски с огибающей эпюрой моментов. На расстоянии не менее 15 диаметров пучка от места теоретического обрыва может быть поставлен внутренний анкер (рис.10, а). Первым от середины балка заанкеривают пучок арматуры из верхнего ряда. Анкеры рекомендуется симметрично размещать относительно продольной вертикальной плоскости симметрии ребра балки. Пучки нумеруют в последовательности их обрывов и в таблице указывают расположение пучков в поперечном сечении нижнего пояса балки (рис. 10, в). Не менее 1/3 пучков доводят до торцов балки, где их заанкеривают.

Хомуты в стенке балки устанавливают с шагом, не превышающим:

10 см — на торцевых участках балки, простирающихся от ее торцов на длину, равную высоте балки, считая от осей опорных частей;

15 см — на приопорных участках, простирающихся от границ концевых участков до четвертей пролета;

20 см ― на среднем участке балки между границами приопорных участков. Наименьший диаметр хомутов на концевых участках балки составляет 10 мм, а на остальных участках ― 8 мм. Трапецеидальные хомуты в уширенных по сравнению со стенкой участках нижнего пояса размещают в соответствии с размещением хомутов в стенке.

При определении мест изменения толщины стенки вычерчивают в масштабе огибающую эпюру поперечных сил для половины балки (рис. 10, г), приближенно считая, что поперечные силы изменяются по длине балка по линейному закону (рис. 10, г). В пределах длины верхней подушки опорной части, т. е. на расстоянии 1 м от торца балки, толщину стенки принимают равной ширине нижнего пояса балки bf (рис. 6, д). В средней части балки толщина стенки может быть принята минимальной, например bmin = 15 см. В промежутке между опорой и точкой, находящейся на расстоянии

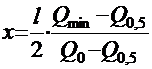
от середины балки, толщина стенки может плавно или ступенчато меняться пропорционально изменению величины поперечной силы (см. рис. 10, д). В приведенной формуле обозначено:

Q0,5 и Q0 — поперечные силы, соответственно, в середине пролета и в опорном сечении;

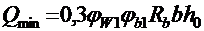― поперечная сила, соответствующая минимальной толщине стенки,

где ;

η = 5 ― при хомутах, нормальных (перпендикулярных) к продольной оси элемента;

n1 ― отношение модулей упругости арматуры хомутов и бетона;

;

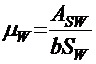АSW ― площадь сечения ветвей хомута, расположенных в одной плоскости;

b ― толщина стенки;

SW ― расстояние между хомутами;

h0 ― рабочая высота сечения;

φb1 = 1 – 0,01Rb;

Rb ― расчетное сопротивление бетона в МПа.

Толщина стенки должна быть назначена с учетом размещения в ней отогнутых пучков арматуры.

2.9 Расчет прочности по поперечной силе

В курсовом проекте прочность балки по поперечной силе разрешается проверить только в одном наклонном сечении, начинающемся на расстоянии 25–30 см от оси опирания и проведенном под углом 25–З5˚ до сжатой зоны бетона, высоту которой принимают из расчета на прочность по изгибающему моменту посередине пролета. Схему конца балки с наклонным сечением изображают в масштабе 1:20 и указывают на ней пересекаемые хомуты и отгибы (рис. 11, а).

Расчетную поперечную силу в конце наклонного сечения приближенно можно определить (рис. 11, б) по формуле:

,

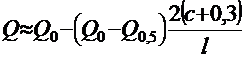где Q0,5 и Q0 — поперечные силы, соответственно, в середине пролета и в опорном сечении;

с ― длина проекции на горизонталь наклонного сечения, м;

l — пролет, м.

Условие прочности наклонного сечения по поперечной силе

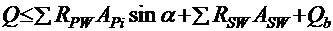, (2.20)

где RPW — расчетное сопротивление напрягаемой арматуры при расчете прочности на поперечную силу;

RSW ― то же, для ненапрягаемой арматуры;

APi — площадь стержня отогнутой напрягаемой арматуры, пересекаемой наклонным сечением;

α ― угол наклона к горизонту отогнутой арматуры;

ASW ― площадь сечения ветвей одного хомута, пересекаемого наклонным сечением;

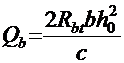(но не более 0,5 Q ) — часть поперечной силы, воспринимаемой сжатой зоной бетона в конце наклонного сечения.

Здесь Rbt — расчетное сопротивление бетона растяжению;

b — ширина ребра балки;

h0 ― рабочая высота балки;

с — длина проекции на горизонталь наклонного сечения, которую можно получить по масштабу непосредственно на чертеже (см. рис. 11, а).

Сначала проверяется прочность наклонного сечения по условию (2.20), считая, что отогнутой арматуры в балке нет. В случае невыполнения этого условия следует отогнуть часть пучков. Количество отгибов должно быть минимальным. Отогнутые пучки располагают в пределах толщины стенки. Угол наклона отгибов составляет 15–20°. Начала отгибов определяют по эпюре изгибающих моментов так же, как и место установки внутреннего анкера. Отгибы располагают симметрично относительно продольной оси балки. После размещения отгибов проверяют по условию (2.20) прочность балки на поперечную силу.

2.10. Расчет на выносливость

Формулы для расчета на выносливость:

а) арматуры растянутой зоны

;

;

;

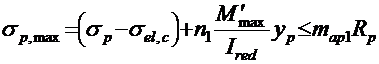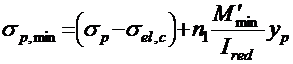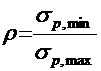б) бетона сжатой зоны

;

;

.

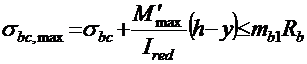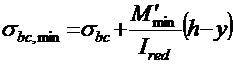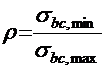В этих формулах:

σp,max и σp,min ― соответственно, максимальные и минимальные напряжения в напрягаемой арматуре;

σp ― установившееся предварительное напряжение в арматуре растянутой зоны, определяемое по формуле (2.9);

σel,c= n1σbp ― снижение напряжений в арматуре от упругого обжатия бетона, где n1 ― отношение модулей упругости арматуры и бетона, σbp ― сжимающее напряжение в бетоне на уровне центра тяжести нижней напрягаемой арматуры, определяемое по формуле (2.12);

map1= ερp ― коэффициент условий работы арматуры, учитывающий влияние многократно повторяющейся нагрузки, где ερp принимается по прил. 9, табл. 9.2;

σbc ― установившееся предварительное напряжение в бетоне сжатой зоны, определяемое по формуле (2.11);

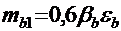― коэффициент условий работы бетона, где βb и εb ― коэффициенты, принимаемые по прил. 8, табл. 8.2 и 8.3;

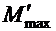и ― и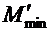згибающие моменты для расчета на выносливость, определяемые по формулам (2.2) и (2.3).

Остальные обозначения пояснены выше.

2. 11. Расчет по трещиностойкости

Предварительно напряженные конструкции железнодорожных пролетных строений должны удовлетворять требованиям по трещиностойкости, характеризующимся в зависимости от их категории значениями растягивающих и сжимающих напряжений в бетоне и расчетной шириной раскрытия трещин. В курсовом проекте достаточно выполнить только некоторые из расчетов по трещиностойкости.

Образование продольных трещин, совпадающих с направлением действия нормальных сжимающих напряжений, во всех конструкциях и на всех стадиях работы недопустимо. Расчет по предотвращению продольных трещин в обжимаемой зоне бетона (т. е. в нижнем поясе балки) в стадии эксплуатации производится по формуле:

,

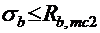где σb — установившиеся предварительные напряжения в бетоне нижней грани балки, определяемые по формуле (2.10);

Rb,mc2 ― расчетное сопротивление осевому сжатию для расчетов по предотвращению продольных трещин на стадии эксплуатации, принимаемое по прил. 8, табл.8.1.

Образование трещин, нормальных к продольной оси элемента, не допускается в конструкциях железнодорожных мостов (категории требований по трещиностойкости 2а), для чего определяют величину напряжений в бетоне:

в стадии эксплуатации у нижней грани балки посередине

пролета

;

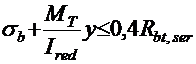в стадии изготовления и хранения у верхней грани балки посередине пролета

;

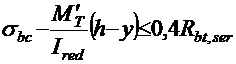где σb и σbc ― установившиеся предварительные напряжения, соответственно, в нижней и верхней гранях балки, определяемые по формулам (2.10) и (2.11);

МТ и — изгибающие моменты для расчета по трещиностойкости, соответственно, в стадиях эксплуатации и изготовления и хранения, рассчитываемые по формулам (2.5) и (2.7);

Rbt,ser ― расчетное сопротивление осевому растяжению бетона при расчетах по предельным состояниям второй группы, принимается по прил. 8, табл. 8.1.

2.12. Расчет на прогиб

Вертикальный прогиб пролетного строения от нормативной временной подвижной вертикальной нагрузки не должен превышать допустимой величины:

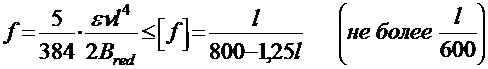
где ε — коэффициент, учитывающий отсутствие тяжелых транспортеров;

ν — нормативная эквивалентная нагрузка от подвижного состава в кН/м (тс/м) пути при длине загружения λ = l и коэффициенте α = 0,5;

l — пролет главных балок, м;

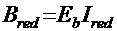― жесткость приведенного сечения одной главной балки, кН•м (тс•м).

Здесь Еb — модуль нормальной упругости бетона (см. прил. 8, табл. 8.4)

Ired ― момент инерции приведенного сечения.

3. РАСЧЕТ УСТОЯ

3.1. Схема устоя

Для расчета и конструирования принимают свайный или рамный устой при высоте насыпи и величине берегового пролетного строения из рекомендованного студентом варианта моста. Свайные устои целесообразно применять при сравнительно небольшой высоте насыпи, не превышающей 8–10 м, и грунтах, допускающих забивку свай (рис. 12, а). При большой высоте насыпи целесообразнее применять рамные устои, свободная длина стоек которых меньше свободной длины свай, с фундаментами мелкого заложения на естественном или свайном основании (рис. 12, б, в).

Конструктивную схему устоя составляют на форматке миллиметровой или клетчатой бумаги в масштабе 1:50 — 1:100 в двух проекциях: вдоль и поперек моста (рис. 13). Отметка верха горизонтальной подферменной площадки (ВП) должна быть ниже отметки подошвы рельса (ПР) на строительную высоту пролетного строения (hС) и высоту опорных частей (hОЧ), принимаемых по прил.3. На расстоянии 0,05 м от торца пролетного строения размещают вертикальную грань шкафной стенки устоя, из точки пересечения которой с проекцией опорной площадки проводят прямую с уклоном 1:10, соответствующую верхней грани ригеля (оголовка). Наименьшее расстояние от вертикальной грани шкафной стенки до грани подферменной площадки

,

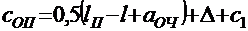где lП ― полная длина пролетного строения, м;

l — расчетный пролет, м;

Δ = 0,05 м — зазор между вертикальной гранью шкафной части устоя и торцом пролетного строения;

аОЧ — размер вдоль моста нижней подушки опорной части, м;

с1 =0,15 м — расстояние от нижней подушки до грани подферменной площадки.

Толщину ригеля (оголовка) принимают достаточной для заделки голов свай или стоек (0,8–1,2 м). Наиболее экономичными по затрате материалов являются устои с одним вертикальным (со стороны насыпи) и одним наклонным (со стороны пролета) рядом свай или стоек с уклоном 1:3 – 1:6. В одном ряду размещают от 2 до 5 свай или стоек квадратного (35х35, 40х40 см) или полого круглого (диаметром 50, 60, 80, 100 или 120 см с толщиной стенки 8–12 см) сечения. Целесообразно принимать меньшее число свай или стоек возможно большего сечения. Данные о сечении и количестве свай или стоек в типовых устоях в зависимости от высоты насыпи приведены в табл. 5.

Наибольшие вертикальные нагрузки на устой передаются через опорные части пролетного строения. Распределение этих нагрузок между рядами свай или стоек зависит от размещения оси опирания пролетного строения относительно центра тяжести площади сечения свай (стоек) в уровне подошвы ригеля (точки "0" на рис. 13). Если ось опирания смещена относительно точки "0" в сторону пролета, то наклонный ряд свай (стоек) окажется более нагруженным, а вертикальный ряд может оказаться даже растянутым, что нежелательно. Если ось опирания смещена в сторону насыпи, то более нагружен вертикальный ряд свай (стоек). Горизонтальные силы давления грунта и торможения подвижного состава направлены в сторону пролета и вызывают дополнительное сжатие свай (стоек) наклонного ряда. В соответствии с распределением усилий следует принять разное количество или сечение свай (стоек) в рядах. Минимальный размер ригеля вдоль моста равен сумме проекций на горизонталь сечений всех свай (стоек), расстояний между ними (минимальное расстояние в свету в уровне низа ригеля между вертикальными сваями или стойками — 2 толщины, а между вертикальной и наклонной сваей или стойкой — 0,5 толщины ствола) и расстояний между сваями (стойками) и гранями ригеля (минимально — 0,25 м). При этом расстоянию от грани подферменной площадки до вертикальной грани ригеля не должно быть менее 0,15 м. Для предотвращения попадания грунта на опорную площадку в пределах длины ригеля применяют защитные боковые стенки. Через точку, находящуюся на 0,5 м ниже угла шкафной части, а при наличии защитных боковых стенок — на 0,5 м ниже верха этих стенок, проводят с уклоном 1:1,5 линию откоса насыпи, а на 0,9 м ниже подошвы рельса проводят горизонтальную линию бровки насыпи. Линия пересечения поверхности конуса насыпи с гранью конструкции устоя должна быть расположена над УВВ не менее чем на 0,5 м.

Шкафная часть устоя представляет собой П–образую в плане железобетонную конструкцию, состоящую из передней шкафной стенки толщиной 0,3–0,4 м и боковых откосных крыльев толщиной 0,2–0,3 м. Верх шкафной стенки на 0,5 м, а откосных крыльев на 0,15 м расположен ниже подошвы рельса. Откосные крылья должны заходить в тело насыпи не менее 0,75 м при высоте на сыпи до 6 м и не менее 1 м — при высоте насыпи свыше 6 м.

Таблица 5

Сечение и количество свай (стоек) в устоях

по типовым проектам № 000 и № 000

*Устой с тремя рядами свай: одним вертикальным и двумя наклонными.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6