Теория поведение потребителей (стр. 3 )

Для данного случая: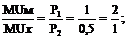

Предельные полезности должны относиться как 2:1. Таких сочетаний несколько:

I сочетание: 1 литр молока (MUм=10) и 3 буханки хлеба (MUх=5), т. е. 1-я и 3-я позиции.

II сочетание: 2 литра молока (MUм=8) и 4 буханки хлеба.

Проверим эти сочетания на бюджетное ограничение (2,5 д. ед.).

I сочетание: 1 литр молока ´ 1д. ед. + 3 буханки хлеба ´ 0,5 = 2,5 д. ед.

II сочетание: 2 литра молока ´ 1д. ед + 4 буханки хлеба ´ 0,5 = 4 д. ед.

Бюджетное ограничение позволяет уравновесить только первое сочетание

Вывод: Q М опт. =1 литр; Q м опт. = Q Хопт. = 3 буханки.

Задача №6 на количественный подход к анализу полезности и определение оптимума потребителя: Марина получает от родителей 6 д. е. в неделю на карманные расходы. Эти деньги она тратит на покупку жвачки и конфет. Каждая жвачка стоит 2 д. е., а каждая конфета – 1 д. е. Полезность для Марины каждую неделю складывается из полезности жвачки и полезности конфет. Две составляющие функции полезности представлены табличным способом:

1) Заполните пропуски в таблице. 2) Какой потребительский набор выберет Марина?

Решение:

1) Заполним таблицу

Ответы получены из простых формул:

Предельная полезность: MU = ∆TU / ∆Q = TUn - TUn – 1 / Qn – Qn – 1;

Взвешенная предельная полезность: MUЖ1/РА; MUК1/РВ и т. д.

2) Марина получит максимум полезности, если распределит свой бюджет:

I = PХ*QХ+ PY*QY так, что МUж/Pж = MUк/Pк, при этом бюджет Марины ограничен 6 д. е.

С учетом бюджетных ограничений оптимальная структура покупки для Марины – это 2 жвачки и 2 конфеты, при этом весь бюджет потребителя истрачен, а структура покупки максимально удовлетворит потребности Марины.

Задача №7 на построение кривых безразличия: Постройте кривые безразличия полезности: 1) для двух взаимодополняющих товаров в пропорции 3 : 1; 2) для двух абсолютно взаимозаменяемых товаров пропорции 3 : 1.

Решение:

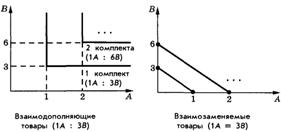
Задача №8 на определение предельной нормы замещения: Найти предельную норму замещения товара У товаром Х при переходе от набора В к набору С.

Решение:

Предельная норма замещения представляет собой то количество одного товара Y, которое потребитель готов заменить единицей другого товара X:

MRS x/y = - Qy/ Qx.

Предельная норма замещения товара У товаром Х при переходе от набора В к набору С равна:

MRS x/y = - Qy/ Qx = - (8-10) / (12-8) = 2 / 4 = 0,5.

Задача №9 на порядковый подход к определению количества благ в оптимальном наборе потребителя: Предельная полезность X для индивида отображается функцией MUХ = 40 – 5*Х, а предельная полезность Y: MUY = 20 – 3*Y. Известны цены благ и доход индивида: PХ = 5; PY=1; I=20. Какое количество каждого из благ должен купить индивид для максимизации общей полезности?

Решение:

Потребитель получит максимум полезности, если распределит свой бюджет:

I = PХ*QХ+ PY*QY так, что MUХ/PХ = MUY/PY.

Получаем систему из двух уравнений:

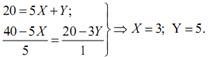
Задача №10 на порядковый подход к анализу полезности и определение цены благ в оптимальном наборе потребителя: Функция полезности для данного потребителя U = 4xy, а доход, выделенный им для покупки данных товаров, равен 24 д. е. В оптимальный набор вошли 2 единицы первого блага (Х) и 3 – второго блага (Y). Чему в этом случае равны цены первого и второго благ?

Решение.

Оптимальный набор должен соответствовать условию бюджетного ограничения:

I = PХ*QХ+ PY*QY 2*Рх + 3*Ру = 24.

Одновременно соотношение цен двух товаров в оптимальм наборе равно соотношению их предельных полезностей: MUx / MUy = Px / Py.

Предельная полезность определяется как первая производная функции полезности:

МUx = dTU / dQХ = 4y; МUy = dTU / dQy = 4x.

Отсюда, МUx = 4*3= 12, МUy = 4*2 = 8.

Поэтому Рх / Ру = 12 / 8 = 3/2.

Можно выразить Рх = 3/2 Ру.

Затем, подставив это выражение в уравнение бюджетного ограничения, получим:

2*Рх + 3*Ру = 24

2 * 3/2 Ру + 3Ру = 24

6Ру = 24

Ру = 4.

Тогда Рх = 3/2 * Ру = 3/2 * 4=6.

Задача №11 на определение уравнения бюджетной линии: Недельный доход Петрова 40 ден. ед. Он расходует его на хлеб и молоко. Вопрос: а) Если цена буханки хлеба 4, а цена литра молока 10, то каково уравнение бюджетной линии; б) как изменится уравнение бюджетной линии, если доход Петрова уменьшится до 20; в) сколько буханок хлеба смог бы купить Петров, если бы отказался от молока.

Решение:

А) Подставим данные из условия задачи в уравнение бюджетной линии:.

4 • Qх + 10 • Qм = 40.

Б) Если доход Петрова уменьшится до 20, то уравнение будет выглядеть:

4 • Qх + 10 • Qм = 20.

В) Если бы Петров отказался от молока, то уравнение будет выглядеть:

4 • Qх + 10 • 0 = 40.

Откуда Qх = 10 буханок.

Задача №12 на анализ бюджетной линии и определение дохода потребителя: На рисунке дана бюджетная линия потребителя. Цена товара Y – 10. Каков доход потребителя?

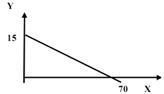
Решение:

Подставим данные из условия задачи в уравнение бюджетной линии: .

Если Х = 0, то весь доход тратится на товар У, количество которого равно 15.

Отсюда доход равен 15 • 10 = 150.

Задача №13 на анализ бюджетной линии и определение функции бюджетного ограничения: На рисунке дана бюджетная линия потребителя с доходом 120 ед. Найти уравнение бюджетной линии.

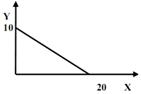
Решение:

Если Х = 0, то весь доход тратится на товар У, количество которого равно 10.

Отсюда цена товара У = 120 / 10 = 12.

Если У = 0, то весь доход тратится на товар Х, количество которого равно 20.

Отсюда цена товара Х = 120 / 20 = 6.

Подставим полученные данные в уравнение бюджетной линии: .

Уравнение бюджетной линии 12 У + 6 Х = 120.

Задача №14 на анализ сдвига бюджетной линии: 1) Чем вызван сдвиг бюджетной линии на рисунке?

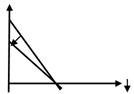
2) Допустим, потребитель имеет доход 1000 д. е. в месяц и весь он должен быть израсходован на покупку двух товаров А и Б. Товар А стоит 25 д. е., а товар Б — 50 д. е. Нарисуйте бюджетную линию (2).

3) Какой будет бюджетная линия (3), если доход потребителя вырастает до 1200 д. е.?

4) Какой будет бюджетная линия (4)при доходе 1000, но снижении цены товара А до 20 д. е.

Решение:

1) Из условия бюджетного ограничения I = PА*QА+ PБ*QБ следует, что сдвиг бюджетной линии (1) на рисунке вызван увеличением цены товара, ведь в этом случае его можно будет купить меньше.

2) Уравнение бюджетной линии (2): 1000 = 25*QА+ 50*QБ.

Бюджетную линию (2) строим по двум точкам:

Если QБ=0, то QА=40;

Если QА=0, то QБ=20.

3) Уравнение бюджетной линии (3): 1200 = 25*QА+ 50*QБ.

Бюджетную линию (3) строим по двум точкам:

Если QБ=0, то QА=48;

Если QА=0, то QБ=24.

4) Уравнение бюджетной линии (4): 1000 = 20*QА+ 50*QБ.

Бюджетную линию строим по двум точкам:

Если QБ=0, то QА=50;

Если QА=0, то QБ=20.

2. 3. 4.

А А А

40 48 50

20 Б 24 Б 20 Б

Задача №15 на порядковый подход к анализу полезности и оптимума потребителя: Предпочтения потребителя заданы в виде функции полезности U(x, y) = xy. Доход равен 800 ден. ед. Цены благ соответственно равны РX = 20, РY= 40. Чему будет равен набор для потребителя? Представьте решение и аналитически, и графически.

Решение.

Запишем задачу в общем виде: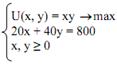

Поскольку оптимум в этом примере является внутренним, то должно выполняться условие

Таким образом, оптимальный набор должен находиться на прямой х = 2у и в то же время удовлетворять бюджетному ограничению.

Получаем систему из 2-х линейных уравнений:

Ее решение дает оптимальный набор: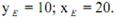

Графическая интерпретация этой задачи:

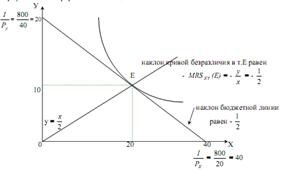
Задача №16 на анализ и построение линии «цена–потребление»: Бюджет индивида равен 200 ден. ед. При цене блага 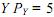его линия «цена–потребление» отображается формулой 1) На сколько единиц индивид изменит потребление каждого блага при снижении цены блага X с 5 до 4 ден. ед.? 2) Используя данные задачи, постройте кривую спроса.

Решение:

1) Ассортимент потребляемых благ определяется точкой пересечения бюджетной линии с линией «цена–потребление» (точкой касания бюджетной линии с кривой безразличия).

Системы уравнений при PX = 5 и PX = 4 соответственно:

Тогда ΔX = 20-18 = 2 ед., ΔY = 24-22 = 2 ед.

2) Пункт 2 выполните самостоятельно.

Задача №17 на анализ линии «доход–потребление» и построение кривой Энгеля: При ценах РX = 4; Рy = 5 линия «доход–потребление» индивида имеет вид: 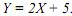1) На сколько единиц индивид увеличит потребление каждого блага при увеличении его бюджета с 333 до 375 ден. ед? 2) Постройте кривую Энгеля.

Решение:

1) Ассортимент потребляемых благ определяется точкой пересечения бюджетной линии с линией «доход–потребление» (точкой касания бюджетной линии с кривой безразличия).

Системы уравнений при бюджетах 333 и 375 ден. ед. соответственно:

Тогда потребление блага X изменится на 25-22 = 3 ед., потребление блага Y изменится на 55-49 = 6 ед.

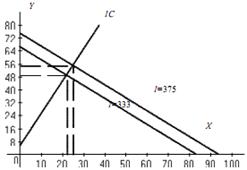
Рис. 1.2. Линия «доход–потребление»

2) Пункт 2 выполните самостоятельно.

3.7. Примеры ответов на тесты

Тест 3.1

Среди следующих утверждений одно является неправильным. Укажите на него:

а) Каждая точка на кривой безразличия означает разную комбинацию двух товаров;

б) Каждая точка на бюджетной линии означает различную комбинацию двух товаров;

в) Все точки на кривой безразличия означают одинаковый уровень удовлетворения потребностей;

г) Все точки на бюджетной линии означают одинаковый уровень денежного дохода;

д) Все точки на кривой безразличия означают одинаковый уровень денежного дохода.

Правильный ответ д).

Данное утверждение является неверным, так как по определению все точки на кривой безразличия означают различные комбинации двух товаров (а), соответствующие одинаковому уровню удовлетворения потребностей (в). Ответы б) и г) относятся к характеристике бюджетной линии и являются верными.

Тест 3.2

Увеличение дохода потребителя графически выражается в:

а) изменении наклона бюджетной линии;

б) параллельном сдвиге бюджетной линии вправо;

в) параллельном сдвиге бюджетной линии влево;

г) уменьшении наклона бюджетной линии;

д) увеличении наклона бюджетной линии.

Правильный ответ б).

Увеличение дохода потребителя означает расширение его возможностей. То есть потребитель получает возможность приобретать большие количества товаров при большем доходе и неизменном уровне цен или при неизменном доходе и снижении цен. Параллельный сдвиг бюджетной линии влево означает уменьшение дохода (в). Изменение наклона бюджетной линии (а): как уменьшение (г), так и увеличение (д) означает изменение в соотношении цен потребляемых благ.

Тест 3.3

Эффект дохода имеет место в следующем случае:

а) Если доходы людей падают, они покупают меньше данного товара;

б) Удешевление товаров приводит к тому, что потребитель может купить больше данного товара, не сокращая объем приобретения других товаров.

В) Объем покупок некоторых товаров сокращается по мере увеличения доходов людей.

Г) По мере того, как доходы людей растут, они сберегают увеличивающуюся часть дохода.

д) Во всех перечисленных случаях.

Правильный ответ б).

Эффект дохода состоит в увеличении возможности удовлетворения потребностей от приобретения товаров либо за счет увеличения дохода при неизменном уровне цен, либо за счет снижения цен при неизменном уровне дохода. Ответ а) и б) определяют сокращение возможностей удовлетворения потребностей. Ответ г) связан с проблемой распределения дохода и характеристикой динамики функции сбережения.

Тема 3.4

Цена товара Х составляет 1,5 руб. Цена товара У составляет 1 руб. Если потребитель оценивает предельную полезность товара У в 30 ютил. И желает максимизировать удовлетворение от покупки товаров Х и У, тогда он должен принять предельную полезность товара Х за:

а) 15 ютил.;

б) 20 ютил.;

в) 30 ютил.;

г) 45 ютил.;

д) В условии не содержится достаточной информации для ответа на вопрос.

Правильный ответ г).

Соотношение цен товаров равно соотношению их предельных полезностей: Mux / Muy = Px / Py. Поэтому Mux = Muy * Px / Py = 30*1,5 / 1 = 45 (ютил).

Тест 3.5

Предположим, что потребитель имеет доход в 8 долл. Цена товара А равна 1 долл., а цена товара В – 0,5 долл. Какая из следующих комбинаций товаров находится на бюджетной линии?

А) 8А и 1В;

б) 7А и 1В;

в) 6А и 6В;

г) 5А и 6В;

д) 4А и 4В.

Правильный ответ г).

Следует исходить из условия бюджетного ограничения: Ра*А + Рв*В = Y. Таким образом, 1* 5 + 0,5* 6 = 8.

Тест 3.6

Общая полезность растет, когда предельная полезность:

а) уменьшается;

б) увеличивается;

в) увеличивается в медленном темпе;

г) увеличивается или уменьшается, но является величиной положительной;
д) является величиной отрицательной.

Правильный ответ г).

Предельная полезность – это прирост общей полезности в расчете на единицу прироста потребления продукта. Общая величина будет увеличиваться до тех пор, пока предельная (прирост) будет иметь положительное значение: если она уменьшается (а) и если она растет (б), даже если растет в медленном темпе (в). Но если предельная величина является отрицательной, общая величина начинает уменьшаться (д).

Тест 3.7

Потребительское равновесие на карте безразличия – это:

а) любое пересечение бюджетной линии и кривой безразличия;

б) любая точка на самой высокой из кривых безразличия;

в) та точка, в которой наклон бюджетной линии равен наклону касательной к ней кривой безразличия;

г) любая точка, расположенная на бюджетной линии;

д) любая точка, расположенная на пространстве, ограниченном бюджетной линией.

Правильный ответ в).

Равновесием потребителя в условиях бюджетных ограничений на графике является точка касания бюджетной линии самой высокой кривой безразличия. Это означает, что в данной точке наклон бюджетной линии и наклон кривой безразличия совпадают. Любое пересечение бюджетной линии и кривой безразличия (а) не может быть равновесием хотя бы потому, что неясно, какую именно кривую безразличия из всей совокупности на карте иметь в виду. Любая точка на самой высокой кривой безразличия (б) может не соответствовать величине бюджета потребителя, а любая точка на бюджетной линии (г) может не являться наилучшей с точки зрения оптимизации потребительских предпочтений.

3.8. Вопросы для самоконтроля

1. Охарактеризуйте общую и предельную полезность: их функции и взаимосвязь. Дайте графическую интерпретацию.

2.  Ответьте на вопрос (парадокс А. Смита): "Почему вода, которая настолько необходима, что без нее невозможно жить, имеет такую низкую цену, в то время как у не столь необходимых алмазов такая высокая цена?"

3.  Почему предельная полезность снижается?

4.  Является ли рациональность естественным свойством человека? Привести примеры нерационального поведения потребителя?

5.  Кардинализм и ординализм — два направления в теории потребительского выбора. Сформулировать их общие черты и различия.

6. Что мы понимаем под кривой безразличия? Какую информацию несет в себе кривая безразличия? Почему такие кривые являются: а) нисходящими; б) выпуклыми по отношению к началу координат?

7.  Какие факторы определяют бюджетное ограничение потребителя? Какую информацию несет бюджетная линия? Как изменится положение бюджетной линии потребителя при уменьшении потребительского дохода? При удорожании блага X? Удешевлении блага У?

8.  Проанализировать, как повлияет на решения потребителей о количестве приобретаемых благ введение Правительством более высоких ставок подоходного налога? Налога с продаж на продукты питания и предметы потребления?

9.  Как можно определить (измерить) общую полезность, если известна предельная

10.  полезность товара?

11.  Каковы условия максимизации общей полезности?

12.  В чем проявляется ограниченность теории предельной полезности?

13.  Как проявляется эффект замещения в случае с гиффеновским товаром?

14.  В чем заключается эффект Веблена?

15.  «Эффект дохода» и «эффект замещения». Возможно ли их действие в противоположных направлениях?

3.9. Литература

Основная литература

1.  Микроэкономика. Теория и российская практика: Учебник / Под ред. ­
вой, . М., КНОРУС, 2004. — Гл. 5.

2.  Вэриан X. Микроэкономика. Промежуточный уровень. Современный подход. —

М.: Юнити, 1997. — Гл. 2—5.

3.  , Игнатьев СМ., Микроэкономика. В 2-х т. — СПб.:
Экономическая школа, 2003. — Т. 1 — Гл. 5.

4.  Курс экономической теории: Учебник / Под общей ред. , ­
левой. — Киров: «АСА», 2002. — Гл.5, §9.

5.  , Экономикс: Принципы, проблемы и политика: в 2-х
томах / Пер. с англ. 13-го изд. — М.: ИНФРА-М, 2001. — Т.2. —Гл.22— 23.

6.  Нуреев P.M. Курс микроэкономики. — М.: Норма-Инфра-М, 2002. — Гл.4.

7.  Общая экономическая теория (политэкономия): Учебник / Под общей ред. В. И.
Видяпина и . — М.: ПРОМО-Медия, 1995. — Гл. 17—18.

Дополнительная литература

1. Алчиан Ар. А. Значение измерения полезности // Теория потребительского поведе­
ния и спроса. — СПб.: Экономическая школа, 1993.

2.  БлаугМ. Экономическая мысль в ретроспективе. — М., 1994. — С.306—343.

3.  Дж., Рынок. Микроэкономическая модель. — СПб., 1992.

— Гл.5.

4.  , Микроэкономика. — М.: ДИС, 1997. — Гл. 5—7.

5.  Микроэкономика. — М.: Дело, 1992. — Гл. 3—4.

6.  Розанова К, Основы экономического выбора. — М.: ТЕИС, 1996.

— Гл.2—5.

7. Суверенитет и рациональность потребителя // Теория потребитель­
ского поведения и спроса. — СПб.: Экономическая школа, 1993.

8.  Франк и поведение. — М.: ИНФРА-М, 2000. — Гл. 3—8.

9.  Хайман микроэкономика: анализ и применение. В 2-х т. — М.:
Финансы и статистика, 1992. — Т.1. — Гл. 3—4.

10.  ХиксДж. Р., Д. Пересмотр теории ценности // Теория потребительского
поведения и спроса. — СПб.: Экономическая школа, 1993.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3