Теория вероятностей и математическая статистика (стр. 1 )

Комитет по образованию Санкт-Петербурга

Государственное образовательное учреждение СПО
Санкт-Петербургский колледж управления и экономики
«Александровский лицей»

ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методические указания
по выполнению расчетного задания

для студентов среднего профессионального образования
специальности 080802 «Прикладная информатика (по отраслям)»

Санкт-Петербург 2010

События A и B – несовместные.

P(A + B) = P(A )+ P(B) = 0,2 +0 ,3 = 0,5

Задача № 2

В колледже 36 карт. Наудачу выбираем карту. Какова вероятность, что выбранная карта ИЛИ Дама, ИЛИ пиковой масти?

А – событие, состоящее в том, что выбранная карта – «ДАМА»

B – событие, состоящее в том, что выбранная карта – «ПИКИ»

A + B – событие, состоящее в том, что выбранная карта ИЛИ Дама, ИЛИ пики. В данном случае А и B совместные события, т. к. наудачу выбранная карта может оказаться дамой пиковой масти.

P(A + B) = P(A) + P(B) – P(AB)

P(A) =

P(B) =

P(AB) = 1/9, т. к. во всех 9 картах пиковой масти, только 1 – дама.

P(A + B) =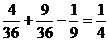

1.5. Условная вероятность

Теорема умножения вероятностей

Р(А/В) – вероятность события В при условии, что событие А уже произошло. Такую вероятность будем называть условной.

Р(А/В) =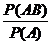

Тогда справедлива теорема умножения вероятностей для зависимых (1) и независимых событий(2)

Р(АВ) = Р(А)*(В/А), (1)

если Р(В/А) = Р(В), то событие В называется независимым от А и

Р(АВ) = Р(А)*Р(В) (2)

Задача № 3

Два стрелка делают по одному выстрелу и попадают по цели с вероятностями соответственно 0,5 и 0,7. Какова вероятность, что хотя бы один стрелок попал?

А – событие, состоящее в том, что попал 1-ый стрелок;

В – событие, состоящее в том, что попал 2-ой стрелок;

АВ – событие, состоящее в том, что И первый, И второй стрелки попали.

= – так можно описать событие, которое состоит в том, что никто не попал. Тогда событие, состоящее в том, что хотя бы один из них попал, будет противоположно событию, состоящему в том, что никто не попал. По свойству вероятностей (4), вероятность Р такого события можно вычислить:

Р = 1 – Р()

Р() = Р()Р()

Р = 1 – 0,5 * 0,3 = 0,85

1.6. Формула полной вероятности

Пусть событие А может произойти только совместно с одним из n попарно несовместимых событий Н1, Н2, …, Нn

НiНj = Æ

А = АН1 + АН2 + … + АНn

Р(А) = 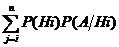– формула полной вероятности.

Hi называют гипотезами

А/Нi называют событием А при условии, что произошла Hi гипотеза

Р(Нi) – вероятность гипотез. Обязательно должно быть, чтобы 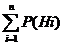= 1

Задача № 4

Пусть имеются 10 урн, в которых 5 белых и 15 черных шаров; 20 урн, в которых 15 белых и 5 черных шаров; 30 урон, в которых 10 белых и 10 черных шаров. Из наудачу выбранной урны наудачу выбрали один шар. Определить вероятность того, что выбранный шар – белый.

Событие А состоит в том, что выбранный шар – белый. Этот шар может быть из урн I типа, II или III типа. Иными словами – событие А наступает совместно с одной из гипотез.

Н1 – гипотеза, состоящая в том, что белый шар вынули из 10 урн I типа.

Н2 – гипотеза, состоящая в том, что белый шар вынули из 20 урн II типа.

Н3 – гипотеза, состоящая в том, что белый шар вынули из 30 урн III типа.

Р(Н1) = = ; Р(Н2) = = ; Р(Н3) = =

=

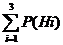Р(А/Н1) = 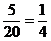– вероятность вынуть белый шар из первых 10 урн.

Р(А/Н2) = 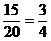, Р(А/Н3) = .

По формуле полной вероятности

Р(А) = =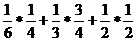

1.7. Формула Байеса (гипотез)

Очень часто необходимо вычислить вероятность гипотезы после наступления события А: Р(Hj/А)

Р(Hj/А) =

Эта формула называется формулой Байеса или формулой гипотез, т. к. позволяет вычислить вероятность гипотезы после опыта через вероятность гипотезы до опыта.

Задача № 5

Пусть комплекс условий S такой же, как в задаче 4. Вынули 1 шар. Он оказался белый. Какова вероятность, что белый шар из первых 10 урн?

До того, как стало известно, что выбранный шар – белый

Р(Н1) = , Р(Н1/А) =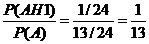

После опыта, когда стало известно, что выбрали белый шар, вероятность гипотезы, что этот шар из первых 10 урн – 1/13

ЗАДАЧА № 2

2.1. Независимые испытания. Формула Бернулли

Пусть комплекс условий S воспроизводится n раз и каждый раз событие A наступает с вероятностью p и не наступают с вероятностью q = 1- p. Для каждого из n независимых испытаний справедливо:

Такая таблица называется индикатором события A

Возникает необходимость вычислить вероятность наступления события A ровно m раз в n независимых повторных испытаниях. Такую вероятность будем обозначать Pmn.

Задача № 6

Всхожесть семян 10%. Посадили 5 семян.

Какова вероятность, что взойдет не менее трех?

A – семян взошло.

Индикатор события A:

Событие, состоящие в том, что взойдет не меньше 3-х семян – это событие, состоящее в том, что взойдет ИЛИ 3, ИЛИ 4, ИЛИ 5 семян.

Следовательно, P(m3) = P3,5 + P4,5 + P5,5

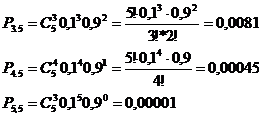
P(m3) = 0,00856 =0 ,86%

2.2. Асимптотические формулы для вычисления Pmn

При больших m и n практически пользоваться формулой Бернулли затруднительно.

Задача № 7

С вероятностью 0,6 лампа выходит из строя после T часов работы. Какова вероятность того, что из 200 ламп останутся исправными более половины?

n = 200, m = 100

P100,200 – вероятность того, что из 200 выйдут из строя 100

Индикатор события A – «ламп несправна»:

P(m>100) = P(m = ИЛИ 101, ИЛИ 102, …, ИЛИ 200) = 1 – P100,200

Вызывает затруднение расчет

В случаях, когда p отличается от нуля, а m и n велики необходимо применить асимптотическую формулу для приближенного вычисления Pmn:

,

где – малая функция Лапласа, значения которой можно найти в таблицах для каждого x.

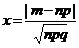
В Задаче № 7 имеем:

np =

m = 100

npq =

(2,89) = 0,0061 (учебник из списка литературы [1], Приложение 2, Таблица 1)

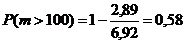
Задача № 8

Книга в 500 страниц содержит 100 опечаток. Какова вероятность того, что на случайно выбранной странице ровно 2 опечатки?

Вероятность того, что на случайно выбранной странице есть опечатка .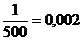

Опечаток всего 100, т. е. число испытаний (опечаток) n = 100, а m = 2.

По формуле Бернулли

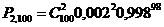
В случаях, так называемых, редких явлений, когда p достаточно мало, а n велико, более точный результат дает другая асимптотическая формула для вычисления

,

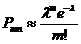Эта формула называется формулой Пуассона, а – параметром распределения. Вычислим P2,100 из задачи 8 по формуле Пуассона.

= np =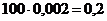

ЗАДАЧА № 3

3.1. Понятие случайной величины и её функция распределения

Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной. Универсальным способом задания случайной величины X является её функции распределения F(X), которая определяется

F(X) = P(X<x)

Функция распределения F(X) случайной величины X – это вероятность того, что случайная величина X примет значение, меньше некоторого конечного числа x.

Задача № 9

Пусть случайная величина X – число выпавших «орлов» при 3-разовом подкидывании монеты. Построить функцию распределения F(X).

Итак, X может принять значения 0, 1, 2, 3 с соответствующими вероятностями P0,3, P1,3, P2,3, P3,3.

Pmn могут быть рассчитаны по формуле Бернулли. Данные расчётов можно свести в таблицу.

Такую таблицу будем называть рядом распределения

= 1, т. к. были рассмотрены все возможные случаи выпадения «орлов» при
3-разовом подкидывании монетки.

Будем строить F(X).

Получилась ступенчатая прерывная (изменяющаяся «скачком» справа) неубывающая функция. Справедливо

P(x1Xx2) = F(x2)-F(x1)

3.2. Дискретная случайная величина и её числовые характеристики

Случайная величина, которая может принимать только конечное или счетное множество значений, называется дискретной. F(X) для дискретной случайной величины имеет график в виде ступенчатой линии, всюду непрерывная слева функция.

Кроме F(X) для описания случайной величины X существуют числовые характеристики.

Математическое ожидание – это среднее значение, которое может принимать случайная величина X по распределению вероятностей обозначается M(X).

Количественно вычисляется по формуле M(X)=

Справедливы следующие свойства математического ожидания

1.  M(C) = C (C – некоторая константа)

2.  M(CX) = CM(X)

3.  M(XY) = M(X) M(Y)

4.  M(XY) = M(X)M(Y)

Задача № 10

Найти среднее значение числа выпавших «орлов» при 3-х разовом подкидывании монетки.

Воспользуемся результатами задачи 9. Из таблицы к задаче 9 можно вычислить

M(X) = =

Дисперсия D(X) – важнейшая числовая характеристика случайной величины X.

D(X) характеризует разброс случайной величины вокруг среднего значения.

D(X) = M(X – M(X))2

Здесь [X – M(X)] – отклонение случайной величины X от M(X). Так как X может отклоняться и в большую, и в меньшую сторону от M(X), то для количественного оценивания D(X), чтобы не учитывать знак, рассматривают «квадрат отклонения».

Удобно пользоваться формулой:

D(X) = M(X2) – [M(X)]2

Рассмотрим свойства дисперсии:

1.  D(C) = 0

2.  D(CX) = C2D(X)

3.  D(X+Y) = D(X) + D(Y)

Задача № 11

Вычислить D(X) для случайной величины X – случайного выпадения числа «орлов» при 3-х разовом подкидывании монетки.

Воспользуемся результатами решения задачи 9. Так как X распределена в соответствии с таблицей к задаче 9,то X2 расположена так же, т. е.

Xi2	0	1	4	9
Pi	1/8	3/8	3/8	1/8

M(X2) = 0 * +

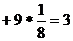
D(X) = M(X2) – [M(X)]2 = 3 –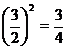

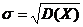– среднеквадратичное отклонение.

Это числовая характеристика введена для вычисления разброса (отклонения) в той же размерности, что и сама случайная величина X.

ЗАДАЧА № 4

4.1. Случайные величины непрерывного типа

Если случайная величина X имеет всюду непрерывно дифференцируемую функцию распределения F(X), то такая случайная величина X называется непрерывной.

F(X)=p(x) Производная от F(X) называется плотностью распределения вероятности.

Непрерывная случайная величина X может быть задана и через функцию распределения, и через ее производную. Очевидно, что

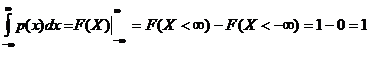
Так как p(x) – это производная от F(X), то F(X)=.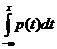

Задача № 12

Плотность распределения непрерывной случайной величины X задана

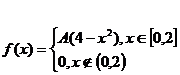
Найти А, F(X) и P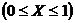

Построим график функции

Для того чтобы распределение было корректно, необходимо чтобы площадь S заштрихованной фигуры равнялась бы 1. Тогда,

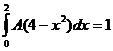
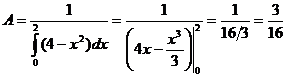
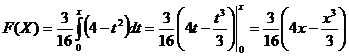
Построим F(X)

X	0	1	2
F(X)	0	11/16	1

4.2. Числовые характеристики непрерывных случайных величин

Если непрерывная случайная величина X принимает любые значения на числовой прямой, то

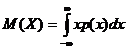
Задача № 13

Вычислить M(X) и D(X) для непрерывной случайной величины X, заданной в задаче 12.

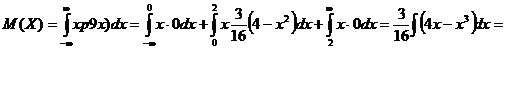
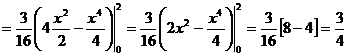
ЗАДАЧА № 5

5.1. Нормальный закон распределения и его характеристики

Случайная величина Х называется распределенной нормально, если плотность распределения вероятностей задается

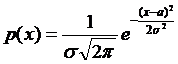
и называются параметрами распределения, причём

M(X)= , D(X)=

Задача № 14

Случайная величина X распределена нормально с параметрами ,=.

Написать функцию p(x),которая является плотностью распределения вероятностей.

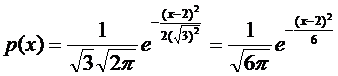
Задание № 15

Случайная величина X задается через плотность распределение вероятностей.

Найти M(X), D(X), A

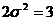Здесь ,следовательно M(X) = –3, , т. е , следовательно D(X) =

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3