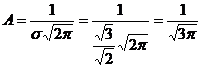Теори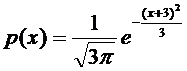я вероятностей и математическая статистика (стр. 2 )

,тогда

5.2. Связь нормального закона распределения с функцией Лапласа

Функцией Лапласа называется функция

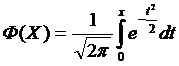
Значение Ф(Х) для любого Х можно найти в учебнике [1] из списка литературы, Приложение 2, Таблица 3.

Функция распределения F(X) для нормальной случайной величины можно вычислить через функцию Лапласа Ф(Х).

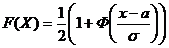
Для вычисления p() также можно пользоваться функцией Лапласа:

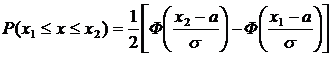
Иногда может быть полезно следующее равенство:

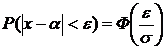
Задача № 16

Случайная величина Х задана плотностью распределения вероятностей в следующем виде

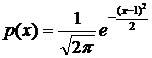
Вычислить вероятность попадания случайной величины на интервал (–3; 3)

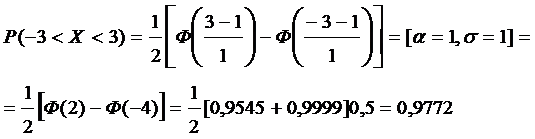
СПИСОК ЛИТЕРАТУРЫ

1.  , , «Теория вероятностей и математическая статистика», Минск.: «Высшая школа», 2003.

2.  Сборник задач по теории вероятностей математической статистике и теории случайных функций, под ред. – М.: Наука, 2000.

3.  , , Кожевникова математика в упражнениях и задачах. М.: «Высшая школа», 2007.

Приложение

Варианты расчетных заданий

Вариант № 1

1. В двух одинаковых урнах содержатся черные и красные шары: в первой – 2 черных и 7 красных, во второй – 5 черных и 10 красных. Из наудачу выбранной урны наудачу извлечен шар, который оказался красным. Найти вероятность того, что извлеченный шар оказался из первой урны.

2. Найти вероятность наступления события в двадцати независимых испытаниях не менее шести раз, если вероятность наступления его в каждом испытании равна 0,8.

3. Определить математическое ожидание М(х), дисперсию D(x), вероятность попадания в интервал (-3,2] (P(-3<X≤2)), если закон распределения дискретной случайной величины Х задан таблицей

Построить график функции распределения F(x)

4. Непрерывная случайная величина Х задана плотностью распределения f(x).Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (0;/2)

f(x)=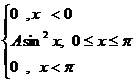

5. Считая, что X – нормально распределенная случайная величина, которая задается функцией плотности распределения

,

найти А, P(|x|>0,5), M(x) ,D(x)

Вариант № 2

1. На складе 200 деталей, из которых 100 изготовлено цехом № 1, 60 – цехом № 2 и 40 – цехом № 3. Вероятность брака для цеха № 1 – 3%, для цеха № 2 – 2% и для цеха № 3 – 1%. Наудачу взятая со склада деталь оказалась бракованной. Найти вероятность того, что эта деталь изготовлена цехом № 2.

2. Вероятность выхода из строя каждого элемента в течение часа равна 0,002. Найти вероятность того, что в течение часа из пятисот элементов выйдут из строя три элемента.

3. Определить математическое ожидание М(х), дисперсию D(x), вероятность попадания в интервал (-3,5] (P(-3<X≤5)), если закон распределения дискретной случайной величины Х задан таблицей

Построить график функции распределения F(x).

4. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (0;1)

f(x)=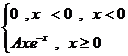

5. Считая, что X – нормально распределенная случайная величина, которая задается функцией плотности распределения

,

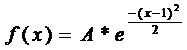найти A, M(x), D(x), P(|x-1|<1,5).

Вариант № 3

1. Предприятие выпускает за смену изделия трёх типов в количестве 160, 430 и 360 штук каждого типа. ОТК ставит штамп либо «БРАК» либо «ЭКСПОРТ». Найти вероятность того, что наудачу взятое изделие пойдёт на экспорт, если вероятности этого для каждого изделия вида I, II или III соответственно равны 0,9, 0,8 и 0,6.

2. Вероятность каждого попадания при выстреле по движущейся мишени равна 0,6. Какова вероятность того, что из 25 выстрелов 10 окажутся удачными?

3. Определить математическое ожидание М(х), дисперсию D(x), вероятность попадания в интеграл 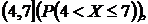если закон распределения дискретной случайной величины Х задан таблицей

Построить график функции распределения F(x).

4. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интеграл (0,1).

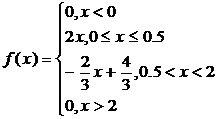
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения

,

найти A, M(x), D(x), P(0<Х<5)

Вариант № 4

1.С двух швейных фабрик поступают на базу внешне одинаковые изделия. С первой фабрики поступает втрое больше изделий, чем со второй. Вероятность брака для изделий первой фабрики 0,1, для изделий второй фабрики – 0,5. Найти вероятность того, что наудачу взятое на базе изделие оказывается не бракованным.

2.Вероятность того, что лампа останется исправной после 1000 часов работы равна 0,2. Найти вероятность того, что хотя бы одна из тех ламп останется исправной после 1000 часов работы.

3. Определить математическое ожидание М(х), дисперсию D(x), вероятность попадания в интервал если закон распределения дискретной случайной величины Х задан таблицей

Построить график функции распределения F(x).

4. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интеграл (1,2).

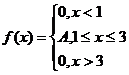
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения

,

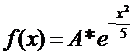найти A, M(x), D(x), P(|x-М(х)|<2).

Вариант № 5

1. С трех конвейеров поступили на склад детали в количестве 150, 300 и 350 штук соответственно. Вероятность брака для детали с первого конвейера – 0,3, со второго – 0,2, и с третьего – 0,2. Наудачу взятая деталь оказалась не бракованной. Найти вероятность того, что эта деталь поступила с третьего конвейера.

2. Вероятность попадания в цель из скорострельного орудия при каждом выстреле равна 0,8. Найти вероятность того, что число попаданий при 900выстрелах будет от 690 до 740.

3. Определить математическое ожидание M(x), дисперсию D(x), вероятность попадания интервал (6,9] (Р(6<Х9)), если закон распределения дискретной случайной величины Х задан таблицей

Построить график функции распределения F(x).

4. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (0,3).

f(x) =

5. Считая, что величина Х – нормально распределенная случайная величина, которая задается функцией распределения

,

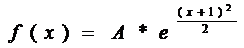найти А, М(х), D(х), P(-3<X<0)

Вариант № 6

1. В классе 30 учеников, из которых 8 отличников и два отстающих. Вероятность решить предложенную задачу для отличника – 0,9, а для отстающего – 0,3, для остальных учеников – 0,7. Наудачу вызванный ученик решил задачу. Какова вероятность того, что это был отличник?

2. Вероятность брака для каждого изделия равна 0,2. Какова вероятность того что, из 6 отобранных изделий число не бракованных будет меньше 3?

3. Определить математическое ожидание М(х), дисперсию D(x), вероятность попадания в интервал (-3,0] (Р(-3<X0)), если закон распределения дискретной случайной величины Х задан таблицей

Построить график функции распределения F(x).

4. Непрерывная случайная величина Х задается плотностью распределения f(x). Найти неизвестный коэффициент A, математическое ожидание, дисперсию интегральную функцию распределения и вероятность попадания Х в интервал (0,/4)

f(x) = ,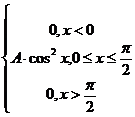

5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения

f(x) = A,

найти A, M(x), D(x), P(1.5<X<3).

Вариант № 7

1. В группе спортсменов 20 лыжников, 6 бегунов и 4 велосипедиста. Вероятность выполнить квалификационную норму для лыжника – 0.8, для бегуна – 0.9, для велосипедиста – 0.8. Наудачу выбранный спортсмен выполнил норму. Найти вероятность того, что спортсмен – лыжник.

2. Вероятность попадания по мишени при каждом выстреле 0.6. Найти вероятность того, что при 30 выстрелах число попаданий будет от 15 до 20.

3. Определить математическое ожидание M(x), дисперсию D(x), вероятность попадания в интервал (-2; 3] (P(-2<X3)), если закон распределения дискретной случайной величины X задан таблицей

Построить график функции распределения F(x)

4. Непрерывная случайная величина X задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (0; 2)

f(x) =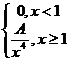

5. Считая, что X – нормально распределенная случайная величина, которая задается функцией распределения

f(x) = A,

найти A, M(x), D(x), P(-2<X<3).

Вариант № 8

1. В двух урнах содержится по 6 белых и 4 красных шара в каждой, в трех других урнах по 5 белых и 3 красных шара в каждой. Из наудачу выбранной урны, наудачу извлекли шар, который оказался красный. Найти вероятность того, что шар оказался из урны первого состава.

2. Прибор состоит из 1000 элементов. Вероятность отказа каждого элемента 0.001. Какова вероятность отказа трех элементов.

3. Определить математическое ожидание M(x), дисперсию D(x), вероятность попадание в интервал (1; 4] (P(1<X4)), если закон распределения дискретной случайной величины Х задан таблицей.

Построить график функции распределения F(x).

4. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (0;.

f(x) =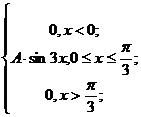

5. Считая, что Х – нормально распределенная случайная величина которая задается функцией распределения

f(x) = A,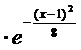

найти A, M(x), D(x) вероятность того, что при трех независимых испытаниях Х дважды попадет в интервал (0; 2).

Вариант № 9

1. Из 14 стрелков пять попадают в мишень с вероятностью 0,8, шесть с вероятностью 0,6 и три с вероятностью 0,7. Наудачу выбранный стрелок произвел выстрел, но в мишень не попал. Какова вероятность того, что стрелок принадлежал ко второй группе стрелков?

2. Всхожесть семян оценивается вероятностью 0,8. Какова вероятность того. Что из пяти посеянных семян взойдет не менее четырех?

3. Определить математическое ожидание M(x), дисперсию D(x), вероятность попадания в интервал (0, 6] (P(0<X6)), если закон распределения дискретной случайной величины Ч задан таблицей

Построить график функции распределения F(x)

4. Непрерывная случайная величина X задана плотностью распределения f(x). Найти математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (1; 2).

f(x)=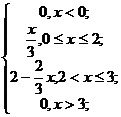

5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения

f(x) = ,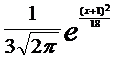

найти M(x), D(x), вероятность того, что при трех независимых испытаниях Х хотя бы раз попадает в интервал (–2; 3)

Вариант № 10

1.На чемпионате по хоккею учреждён приз «лучший бомбардир». Участвуют четыре команды по 12 форвардов в каждой. Вероятность получения приза для форварда из первой команды – 1/2,из второй – 1/3,из третьей – 1/4 и из четвёртой – 1/6.Какова вероятность, что обладатель приза представляет команду № 2?

2. По данным ОТК ан сотню металлических брусков, заготовленных для обработки, 30 приходится с зазубринами. Найти вероятность того, что из случайно отобранных 7 брусков без дефекта окажутся не более двух.

3. Определить математическое ожидание M(x), дисперсию D(x), вероятность попадания интервал (-5; 2] (P(-5<X2)), если закон распределения дискретной случайной величины X задан таблицей.

Построить график функции распределения F(x).

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3