4. Непрерывная случайная величина X задана плотностью распределения f(x). Найти неизвестный коэффициент A, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (0,2).
f(x)=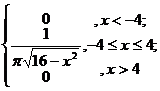
5. Считая, что X – нормально распределённая случайная величина, которая задаётся функцией распределения
f(x)=
,
найти A, M(x), D(x), вероятность того, что при четырёх независимых испытаниях X ни разу не попадет в интервал (0, 2).
Вариант № 11
1. Вероятность попадания при каждом выстреле для трёх стрелков равны соответственно 4/5, 3/4, 2/3. При одновременном выстреле всех трёх стрелков имелось два попадания. Определить вероятность того, что промахнулся третий стрелок.
2. Вероятность появления события A в каждом испытании постоянна и равна 0,6. Найти вероятность того, что в результате 7 опытов событие A появилось не менее двух раз.
3. Определить математическое ожидание M(x), дисперсию D(x), вероятность попадания интервал (-7, 4] (P(-7<X
4)), если закон распределения дискретной случайной величины X задан таблицей
X | –8 | –3 | 0 | 1 | 5 |
P | 0,2 | 0,1 | 0,3 | 0,2 | 0,2 |
Построить график функции распределения F(x).
4. Непрерывная случайная величина X задана плотностью распределения f(x). Найти неизвестный коэффициент A, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (5; 6).
f(x)=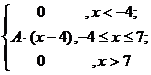
5. Считая, что X – нормально распределённая случайная величина, которая задаётся функцией распределения
,
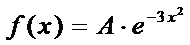найти A, M(x), D(x), P(|X|<0,5).
Вариант № 12
1. Три зенитки выстрелили одновременно по самолету, и в результате произошло одно попадание. Найти вероятность того, что самолет сбит второй зениткой, если вероятности попадания для каждого орудия равны соответственно 0,2, 0,3, 0,4.
2. Стрелок стреляет по мишени 7 раз. Вероятность попадания при отдельном выстреле 0,8. Определить вероятность того, что произошло не менее 2 и не более 5 попаданий.
3. Определить математическое ожидание M(x), дисперсию D(x), вероятность попадания интервал (-3; 4] (P(-3<x4)), если закон распределения дискретной величины X задан таблицей
X | -5 | -2 | -1 | 0 | 4 |
P | 0,1 | 0,1 | 0,4 | 0,3 | 0,1 |
Построить график функции распределения F(x).
4. Непрерывная случайная величина X задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (2; 4).
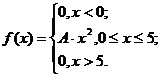
5. Считая, что X нормально распределенная случайная величина, которая задается функцией распределения
,
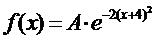найти A, M(x), D(x), P(
<0,5).
Вариант № 13
1. В трех одинаковых ящиках – шары двух цветов: в первом – 10 шаров, из них 7 зеленых, во втором –зеленых), в третьем –зеленых). Из наудачу выбранного ящика взяли два шара. Определить вероятность того, что они одного цвета.
2. Игральная кость бросается 6 раз. Определить вероятность того, что грань с тремя очками выпадет не менее двух и не более четырех раз.
3. Определить математическое ожидание M(x), дисперсию D(x), вероятность попадания интервал 
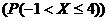, если закон распределения дискретной случайной величины X задан таблицей
X | –2 | –1 | 0 | 4 | 6 |
P | 0,2 | 0,3 | 0,2 | 0,1 | 0,2 |
Построить график функции распределения F(x).
4. Непрерывная случайная величина X задана плотностью распределения f(x). Найти неизвестный коэффициент A, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал 
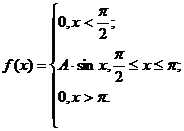
5. Считая, что X – нормально распределенная случайная величина, которая задается функцией распределения
,
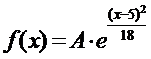найти A, M(x), D(x), P(-10<X<3).
Вариант № 14
1. Стрелок делает столько выстрелов, сколько «орлов» выпадет на двух монетах. Вероятность попадания при каждом выстреле у него равна 0,8. Какова вероятность того, что он не попадет ни разу?
2 .Для поражения цели достаточно двух попаданий. Произведено три выстрела. Определить вероятность поражении цели, если при одном выстреле вероятность попадания 0,8.
3. Определить математическое ожидание M(x), дисперсию D(x), вероятность попадания интервал (-8; 0]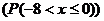 
, если закон распределения дискретной случайной величины X задан таблицей
X | –10 | –8 | –5 | 0 | 6 |
P | 0,2 | 0,2 | 0,3 | 0,1 | 0,2 |
Построить график функции распределения F(x).
4. Непрерывная случайная величина X задана плотностью распределения f(x). Найти неизвестный коэффициент A, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (-1; 0).
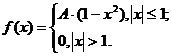
5. Считая, что X– нормально распределенная случайная величина, которая задается функцией распределения
,
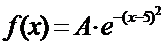найти A, M(x), D(x),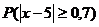 
Вариант № 15
1. Имеется 3 одинаковых урны. В первой 11 белых и 7 красных шаров, во второй 4 белых и 5 красных, в третьей 8 белых и 10 красных шаров. Из наудачу выбранной урны взяли 2 шара. Они оказались белыми. Найти вероятность того, что извлечение произведено из первой урны.
2. Вероятность брака для каждого изделия равна 0,3. Какова вероятность, что при проверке серии изделий первое бракованное изделие окажется шестым из проверенных?
3. Определить математическое ожидание М(х), дисперсию D(x), вероятность попадания интервал (-7,4] (Р(-7<Х 14)), если закон распределения дискретной случайной величины X задан таблицей
X | –7 | 2 | 3 | 4 | 5 |
P | 0,1 | 0,3 | 0,4 | 0,1 | 0.1 |
Построить график функции распределения F(x).
4. Построить график функций распределения f(x). Непрерывная случайная величина X задана плотностью распределения f(х). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (π/2; 3π 4).
f(x) =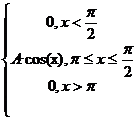 
5.Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения
f(x)=A·e x2,
найти А, М(х), D(x), p(-1<X<1).
Вариант № 16
1. Стрелок сделал столько выстрелов, сколько «орлов» выпало на двух монетах, и попал ровно 1 раз. Вероятность попадания у него равна 0,7. Какова вероятность, что был сделан только 1 выстрел?
2. Какова вероятность, что в записи семизначного числа содержится ровно 3 единицы?
3. Определить математическое ожидание М(х), дисперсию D(x), вероятность попадания в интервал (0; 7] (Р(0<Х≤7)), если закон распределения дискретной случайной величины X задан таблицей
X | –1 | 0 | 2 | 4 | 7 |
р | 0,2 | 0,1 | 0,1 | 0,3 | 0,3 |
Построить график функции распределения F(x).
4. Непрерывная случайная величина X задается плотностью распределения f(х). Найти неизвестный коэффициент А. математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (1; 3).
f(x)=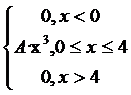 
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения
f(x)=A·
,
найти А, М(х), D(x), P(0<X<3).
Вариант № 17
1. Баскетболист, бросив игральную кость, делает столько бросков по корзине, сколько очков выпало на игральной кости. Какова вероятность того, что при этом будет ровно три попадания, если вероятность попадания при каждом броске равна 0,6?
2. Баскетболист делает 6 бросков по корзине. Вероятность попадания при каждом броске 0,8. Определить вероятность того, что произошло не менее двух попаданий?
3. Определить математическое ожидание М(х). дисперсию D(x), вероятность попадания в интервал (-1; 5] (Р(-1<X
)), если закон распределения дискретной случайной величины Х задан таблицей
X | -3 | -1 | 2 | 4 | 5 |
P | 0,4 | 0,3 | 0,1 | 0,1 | 0,1 |
Построить график функции распределения F(x).
4. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (0; 2).
f(x) =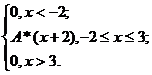 
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения
F(x) = A *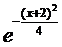 
,
найти А, М(х), D(x), P(-3<X<-1).
Вариант № 18
1. С первого автомата поступает 45% деталей, со второго – 30%;. с третьего – 25%. Среди деталей первого автомата 5% негодных, второго – 10%, третьего – 8%. Поступившая на сборку деталь годная. Какова вероятность, что шестерка выпадет 25 или 21 раз?
2. Игральную кость бросают 125 раз. Какова вероятность, что шестерка выпадет 25 или 21 раз?
3. Определить математическое ожидание М(х), дисперсию D(х), вероятность попадания на интервал (3,8] (Р(3<X
), если закон распределения дискретной случайной величины Х задан таблицей
X | 1 | 3 | 4 | 7 | 8 |
P | 0,5 | 0,1 | 0,1 | 0,2 | 0,1 |
Построить график функции распределения F(X).
4. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (-2; 0).
f(x)=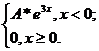
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения
F(x) = A*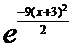
,
найти А, М(х), D(x), P(-3<X<3).
Вариант № 19
1. Бросили три монеты. Стрелок делает столько выстрелов, сколько выпало на них «орлов». Вероятность попадания при одном выстреле равна 0,6. Какова вероятность, что стрелок попадет ровно два раза?
2. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,8. Найти вероятность того, что 21-е попадание будет ровно в 26-м выстреле.
3. Определить математическое ожидание М(х), дисперсию D(х), вероятность попадания интервал (2; 5] (Р(2<X5)), если закон распределения случайной величины Х задан таблицей
X | 0 | 2 | 3 | 5 | 6 |
P | 0,3 | 0,2 | 0,1 | 0,2 | 0,2 |
Построить график функции распределения F(x)
4. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (0; 4).
f(x) =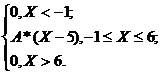 
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения
f(x) = A *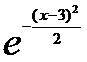 
,
найти А, М(х), D(x), Р(о<X<2).
Вариант № 20
1. Вероятности попадания при каждом выстреле для трех стрелков равны соответственно 0,4, 0,5, 0,6. При одновременном выстреле всех трех стрелков имелось два промаха. Определить вероятность того, что попал третий стрелок.
2. Игральную кость бросают 5 раз. Какова вероятность того, что «двойка» выпадет меньше двух раз?
3. Определить математическое ожидание М(х), дисперсию D(х), вероятность попадания на интервал (-4; 5] (Р(-4<Х)), если закон распределения дискретной случайной величины Х задан таблицей
X | -4 | -3 | 0 | 5 | 7 |
P | 0,2 | 0,1 | 0,3 | 0,3 | 0,1 |
Построить график функции распределения F(x).
4. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (-3; -2).
f(x) =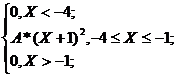 
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения
f(x)= A*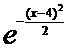 
,
найти А, M(x), D(x), P(|X|<3).
Вариант № 21
1. Имеются три одинаковые урны. В первой 12 зеленых и 8 красных шаров, во второй 8 зеленых и 8 красных шаров, в третьей 12 зеленых и 4 красных шара. Из наудачу выбранной урны взяли 2 шара. Они оказались разноцветными. Найти вероятность того, что извлечение произведено из второй урны.
2. Для поражения танка достаточно трех попаданий. Произведено 5 выстрелов. Определить вероятность поражения танка, если вероятность попадания при одном выстреле 0,6.
3. Определить математическое ожидание M(x), дисперсию D(х), вероятность попадания интервал (1; 5] (P(1<X5)), если закон распределения дискретной случайной величины Х задан таблицей
X | 1 | 4 | 5 | 8 | 10 |
P | 0,4 | 0,3 | 0,1 | 0,1 | 0,1 |
Построить график функции распределения F(x)
4. Непрерывная случайная величина X задана плотностью распределения f(x). Найти неизвестный коэффициент A, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (
).
f(x)=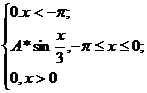
5. Считая, что X – нормально распределенная случайная величина, которая задается функцией распределения
f(x)=A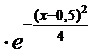
,
найти A, M(x), D(x), P(|X|<2).
Вариант № 22
1. В урне 5 белых и 15 черных шаров. Стрелок вытаскивает 2 шара, затем делает столько выстрелов; сколько среди них белых. Вероятность попадания при отдельном выстреле для него 0,8. Определить вероятность того, что он не попал ни раз.
2. Вероятность попадания в корабль при одном выстреле равна 0,05. Для поражения корабля необходимо 4 попадания. Произведено 100 выстрелов. Какова вероятность того, что корабль остался на плаву?
3. Определить математическое ожидание М(x), дисперсию D(x), вероятность попадания в интервал (-5; 4] (Р(-5<X4)), если закон распределения дискретной случайной величины X задан таблицей
Х | –9 | –5 | –3 | 0 | 4 |
Р | 0,3 | 0,3 | 0,2 | 0,1 | 0,1 |
Построить график функции распределения F(x).
4. Непрерывная случайная величина Х задается плотностью распределения f(x). Найти неизвестный коэффициент А., математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервал (1; 1,5).
f(x)=
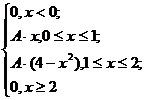
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения
,
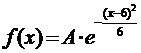найти А, М(х), D(x), P(1<X<4).
Вариант № 23
1.В трех одинаковых ящиках шары двух цветов: в первом ящике 8 шаров, из них 5 белых, во втором – 7 (4 белых), в третьем 9 (6 белых). Из них наудачу выбранного ящика взяли 2 шара разного цвета. Найти вероятность того, что шары из третьего ящика.
2. Какова вероятность, что при бросании шести монет «орел» откроется более чем на двух?
3. Определить математическое ожидание М(х), дисперсию D(х), вероятность попадания интервал (3; 9] (Р(3<Х9)), если закон распределения дискретной случайной величины Х задан таблицей
Х | 1 | 3 | 4 | 7 | 9 |
Р | 0,2 | 0,4 | 0,2 | 0,1 | 0,1 |
Построить график функций распределения F(x).
4. Непрерывная случайная величина Х задана полностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (-
,0).
f(x)=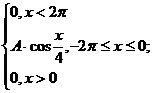
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения
,
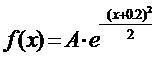найти А, М(х), D(x), P(-1<X<2).
Вариант № 24
1. Два автомата производят детали, поступающие на общий конвейер. Вероятность изготовления дефектной детали первым автоматом равна 0,15, а вторым 0,2. Производительность второго автомата вдвое больше первого. Найти вероятность того, что поступившая на конвейер деталь годная.
2. Электронный экзаменатор задает 5 вопросов. Вероятность правильного ответа на любой из них равна 0,8. Какова вероятность, что будут правильные ответы более чем на три вопроса?
3. Определить математическое ожидание М(х), дисперсию D(х), вероятность попадания в интервал (-5; 4] (P(-5<X4)), если закон распределения дискретной случайной величины Х задан таблицей
Х | -5 | -3 | 0 | 4 | 6 |
Р | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
Построить график функций распределения F(x).
4. Непрерывная случайная величина Х задается плотностью распределения f(x). Найти неизвестный коэффициент А., математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания Х в интервал (-3; 2).
f(x)=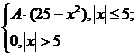
5. Считая, что Х – нормально распределенная случайная величина, которая задается функцией распределения
,
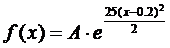найти A, M(x), D(x), P(-0.1<X<0.4).
Вариант № 25
1. Бросили три монеты. Баскетболист сделал столько бросков, сколько на них выпало «орлов». Вероятность попадания при одном броске 0,6. Какова вероятность того, что баскетболист попал 1 раз?
2. Производятся испытания прибора. При каждом из них прибор может дать отказ с вероятностью 0,1. После первого отказа прибор ремонтируется, после второго признается негодным. Найти вероятность того, что прибор будет признан негодным на шестом испытании.
3. Определить математическое ожидание М(x), дисперсию D(x), вероятность попадания в интервал (1; 4] (P(1<X≤4)), если закон распределения дискретной случайной величины X задан таблицей
X | –3 | –1 | 2 | 4 | 8 |
P | 0,1 | 0,3 | 0,2 | 0,1 | 0,3 |
Построить график функции распределения F(x).
4. Непрерывная случайная величина X задана плотностью распределения f(x). Найти неизвестный коэффициент А, математическое ожидание, дисперсию, интегральную функцию распределения и вероятность попадания X в интервале (0; 1)
f(x)=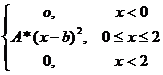 
5. Считая, что X – нормально распределенная случайная величина, которая задается функцией плотности распределения
f(x)=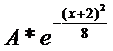
,
найти A, M(x), D(x), P(|x|)<3).
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 |
