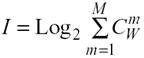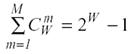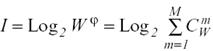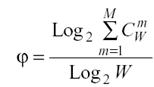Вертикальный портал | Федеральный образовательный портал | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Элементы ИС, рассмотренные в матрице:
1. Доступ
2. Язык программирования
3. Информация
4. Каталогизация
5. Защита информации
6. Взаимодействие
7. Программные продукты
8. Администрирование
9. Управление
10. Поиск
Сравнивалась проектируемая ИС с порталом www. *****
Рис.1.1.1. Матрица Александера (фрагмент)
Количество элементов, подлежащих полной замене | 0 |
Количество элементов, подлежащих модернизации | 39 |
Количество элементов, не подлежащих замене | 57 |
ВСЕГО: | 96 |
Таблица 1. Элементы соответствия-несоответствия
Таким образом, из таблицы 1 видно, что коэффициент абсолютной добротности системы по отношению к контенту равен 57/96 = 0,59. Коэффициент относительной добротности равен (57+39)/96 = 1.
Полученные значения существенно превышают величину относительной энтропии контента, равную 0,47, подсчитанную на предыдущей стадии полного менеджмента проекта. Следовательно, контент проектируемой системы релевантен по отношению к опорному базовому Федеральному образовательному порталу.
1.3. Эмерджентность системы
В классической теории информации Шеннона, созданной на основе обобщения результатов Больцмана, Найквиста и Хартли, само понятие информации определяется на основе теоретико-множественных и комбинаторных представлений на основе анализа поведения классического макрообъекта, который может переходить только в четко фиксированные альтернативные редуцированные состояния. Однако, квантовые объекты и сложные активные рефлексивные системы могут оказываться одновременно в двух и более альтернативных для классических объектов состояниях. Такие состояния будем называть смешанными. Таким образом наблюдается картина последствий, не сводящаяся к простой сумме последствий альтернативных вариантов, т. е. очень напоминающая квантовое физическое явление, которое называется интерференцией плотности вероятности. Это явление, безусловно имеющее системный характер, предлагается называть "интерференция последствий выбора".
Предлагается обобщение классической теория информации Хартли-Шеннона путем рассмотрения квантовых и активных объектов в качестве объектов, на основе анализа которых формируется само основополагающее понятие информации. Обобщенную таким образом теорию информации предлагается называть системной или эмерджентной теорией информации. Основным отличием эмерджентной теории информации от классической является учет свойства системности, как фундаментального и универсального свойства всех объектов, на уровне самого понятия информации, а не только в последующем изложении, как в классической теории.
Классическая формула Хартли имеет вид:
| (3. 1) |
Будем искать ее системное обобщение в виде:
| (3. 2) |
где:
W – количество чистых (классических) состояний системы.
j – коэффициент эмерджентности Хартли (уровень системной организации объекта, имеющего W чистых состояний);
Учитывая, что возможны смешанные состояния, являющиеся нелинейной суперпозицией или одновременной реализацией чистых (классических) состояний "из W но m", всего возможно 
состояний системы, являющихся сочетаниями классических состояний.
Таким образом, примем за аксиому, что системное обобщение формулы Хартли имеет вид:
| (3. 3) |
Так как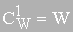 
, то при M=1 выражение (3.3) приобретает вид (3.1), т. е. выполняется принцип соответствия, являющийся обязательным для более общей теории.
Рассмотрим подробнее смысл выражения (3.3), представив сумму в виде ряда слагаемых:
| (3. 4) |
Первое слагаемое в (3.4) дает количество информации по классической формуле Хартли, а остальные слагаемые – дополнительное количество информации, получаемое за счет системного эффекта, т. е. за счет наличия у системы иерархической структуры или смешанных состояний. По сути дела эта дополнительная информация является информацией об иерархической структуре системы, как состоящей из ряда подсистем различных уровней сложности.
Учитывая, что при M=W:
| (3.5) |
Т. к. при W>4 ошибки незначительна, то получаем:
|
Приравняв правые части выражений (3.2) и (3.3):
| (3.8) |
получим выражение для коэффициента эмерджентности Хартли:
| (3. 9) |
или при M=W и больших W, учитывая (3.4 – 3.6):
|
Коэффициент эмерджентности Хартли представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем, системы запретов и т. п.) над количеством информации без учета системности, то есть этот коэффициент отражает уровень системности объекта. Коэффициент эмерджентности Хартли отражает уровень системности объекта и изменяется от единицы (системность минимальна, то есть отсутствует) до отношения W/LogW по основанию 2, где W - количество чистых классических (вне запретов) состояний системы (системность максимальна). Очевидно, для каждого количества элементов системы существует свой максимальный уровень системности, который никогда реально не достигается из-за правил запрета на реализацию в системе ряда подсистем различных уровней иерархии в ансаблях уровней иерархии системы.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |
