Кодирование текстовой информации

Для удобства представления информации в компьютере все возможные виды информации переводятся в числовую форму, и эти числа хранятся в компьютере в двоичном виде, т. е. кодируются.

Кодирование информации — процесс преобразования информации из формы, удобной для непосредственного использования, в форму, удобную для передачи, хранения или автоматической переработки.

Кодирование текстовой информации

Для записи текстовой (знаковой) информации всегда используется какой-либо язык (естественный или формальный).

Всё множество используемых в языке символов называется алфавитом. Полное число символов алфавита N называют его мощностью. При записи текста в каждой очередной позиции может появиться любой из N символов алфавита, т. е. может произойти N событий. Следовательно, каждый символ алфавита содержит i бит информации, где i определяется из неравенства (формула Хартли): 2i ≥ N. Тогда общее количество информации в тексте определяется формулой:

V = k * i , 

где V – количество информации в тексте; k – число знаков в тексте (включая знаки препинания и даже пробелы),  i- количество бит, выделенных на кодирование одного знака.

Так как каждый бит – это 0 или 1, то любой текст может быть представлен последовательностью нулей и единиц. Именно так  текстовая информация хранится в памяти компьютера. Присвоение символу алфавита конкретного двоичного кода - это вопрос соглашения, зафиксированного в кодовой таблице. В настоящее время широкое распространение получили кодовые таблицы ASCII и Unicode.

ASCII (American Standart Code for Informational Interchange - Американский стандартный код информационного обмена) используется достаточно давно. Для хранения кода одного символа выделено 8 бит, следовательно, кодовая таблица поддерживает до 28 = 256символов. Первая половина таблицы (128 символов) - управляющие символы, цифры и буквы латинского алфавита. Вторая половина отводится под символы национальных алфавитов. К сожалению, в настоящее время существует целых пять вариантов кодовых таблиц для русских букв (КОИ-8, Windows-1251, ISO, DOS, MAC), поэтому тексты созданные в одной кодировке неверно отображаются в другой. (Наверное, Вы встречали русскоязычные сайты, тексты которых выглядят как бессмысленный набор знаков?).

Unicode - получил распространение в последние годы. Для хранения кода одного символа выделено 16 бит, следовательно, кодовая таблица поддерживает до 216 = 65536 символов. Такого пространства достаточно, чтобы в одном стандарте объединить все "живые" официальные (государственные) письменности. Кстати, стандарт ASCII вошел в состав Unicode.

Если кодирование – это перевод информации с одного языка на другой (запись в другой системе символов, в другом алфавите), то декодирование – обратный перевод.

При кодировании один символ исходного сообщения может заменяться одним символом нового кода или несколькими символами, а может быть и наоборот – несколько символов исходного сообщения заменяются одним символом в новом коде (китайские иероглифы обозначают целые слова и понятия), поэтому кодирование может быть равномерное и неравномерное. При равномерном кодировании все символы кодируются кодами равной длины, при неравномерном кодировании разные символы могут кодироваться кодами разной длины, что затрудняет декодирование.

Закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова. Закодированное сообщение можно однозначно декодировать с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова. Условие Фано – это достаточное, но не необходимое условие однозначного декодирования.

Решение задач на кодирование текстовой информации

1.Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке длиной в 20 символов, первоначально записанного в 2-байтном коде Unicode, в 8-битную кодировку КОИ-8. На сколько бит уменьшилась длина сообщения? В ответе запишите только число.

Решение:

1)  при 16-битной кодировке объем сообщения – 16*20 бит

2)  когда его перекодировали в 8-битный код, его объем стал равен– 8*20 бит

3)  таким образом, сообщение уменьшилось на 16*20 – 8*20 = 8*20 = 160 бит

Ответ: 160

2. Определите информационный объем текста в битах

Бамбарбия! Кергуду!

Решение:

1)  в этом тексте 19 символов (обязательно считать пробелы и знаки препинания)

2)  если нет дополнительной информации, считаем, что используется 8-битная кодировка (чаще всего явно указано, что кодировка 8- или 16-битная), поэтому в сообщении 19*8 = 152 бита информации

Ответ: 152

3. В таблице ниже представлена часть кодовой таблицы ASCII:

Каков шестнадцатеричный код символа «q»?

Решение:

1)  в кодовой таблице ASCII все заглавные латинские буквы A-Z расставлены по алфавиту, начиная с символа с кодом 65=4116

2)  все строчные латинские буквы a-z расставлены по алфавиту, начиная с символа с кодом 97=6116

3)  отсюда следует, что разница кодов букв «q» и «a» равна разнице кодов букв «Q» и «A», то есть, 5116 – 4116=1016

4)  тогда шестнадцатеричный код символа «q» равен коду буквы «a» плюс 1016

5)  отсюда находим 6116 + 1016=7116.

Ответ: 71

4. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–00, Б–010, В–011, Г–101, Д–111. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.

1) для буквы Б –это невозможно

3) для буквы В –для буквы Г – 01

Решение (1 способ - проверка условий Фано):

1)  для однозначного декодирования достаточно, чтобы выполнялось одно из условий Фано: прямое или обратное условие Фано;

2)  проверяем последовательно варианты 1, 3 и 4; если ни один из них не подойдет, придется выбрать вариант 2 («это невозможно»);

3)  проверяем вариант 1: А–00, Б–01, В–011, Г–101, Д–111.

«прямое» условие Фано не выполняется (код буквы Б совпадает с началом кода буквы В);

«обратное» условие Фано не выполняется (код буквы Б совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит;

4)  проверяем вариант 3: А–00, Б–010, В–01, Г–101, Д–111.

«прямое» условие Фано не выполняется (код буквы В совпадает с началом кода буквы Б);

«обратное» условие Фано не выполняется (код буквы В совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит;

5)  проверяем вариант 4: А–00, Б–010, В–011, Г–01, Д–111.

«прямое» условие Фано не выполняется (код буквы Г совпадает с началом кодов букв Б и В); но «обратное» условие Фано выполняется (код буквы Г не совпадает с окончанием кодов остальных буквы); поэтому этот вариант подходит;

Ответ: 4

Решение (2 способ, дерево):

1)  построим двоичное дерево, в котором от каждого узла отходит две ветки, соответствующие выбору следующей цифры кода – 0 или 1; разместим на этом дереве буквы А, Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах, составляющих путь от корня до данной буквы (красным цветом выделен код буквы В – 011):

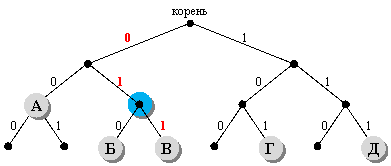
2)  здесь однозначность декодирования получается за счёт того, что при движении от корня к любой букве в середине пути не встречается других букв (выполняется условие Фано);

3)  теперь проверим варианты ответа: предлагается перенести одну из букв, Б, В или Г, в узел с кодом 01, выделенный синим цветом

4)  видим, что при переносе любой из этих букв нарушится условие Фано; например, при переносе буквы Б в синий узел она оказывается на пути от корня до В, и т. д.; это значит, что предлагаемые варианты не позволяют выполнить прямое условие Фано

5)  хочется уже выбрать вариант 2 («это невозможно»), но у нас есть еще обратное условие Фано, для которого тоже можно построить аналогичное дерево, в котором движение от корня к букве дает её код с конца (красным цветом выделен код буквы В – 011, записанный с конца):

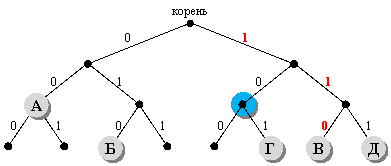
видно, что обратное условие Фано также выполняется, потому что на пути от корня к любой букве нет других букв

6)  в заданных вариантах ответа предлагается переместить букву Б, В или Г в синий узел; понятно, что Б или В туда перемещать нельзя – перемещённая буква оказывается на пути от корня к букве Г; а вот букву Г переместить можно, при этом обратное условие Фано сохранится

Ответ: 4

5. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код: А–1, Б–000, В–001, Г–011. Укажите, каким кодовым словом должна быть закодирована буква Д.. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования.

1)) 010

Решение:

7)  заметим, что для известной части кода выполняется условие Фано – никакое кодовое слово не является началом другого кодового слова

8)  если Д = 00, такая кодовая цепочка совпадает с началом Б = 000 и В = 001, невозможно однозначно раскодировать цепочку 000000: это может быть ДДД или ББ; поэтому первый вариант не подходит

9)  если Д = 01, такая кодовая цепочка совпадает с началом Г = 011, невозможно однозначно раскодировать цепочку 011: это может быть ДА или Г; поэтому второй вариант тоже не подходит

10)  если Д = 11, условие Фано тоже нарушено: кодовое слово А = 1 совпадает с началом кода буквы Д, невозможно однозначно раскодировать цепочку 111: это может быть ДА или ААА; третий вариант не подходит

11)  для четвертого варианта, Д = 010, условие Фано не нарушено;

Ответ: 4.

6. Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится

1) 4B16BACD16

Решение:

1)  из условия коды букв такие: A – 00, Б –01, В – 10 и Г – 11, код равномерный;

2)  последовательность БАВГ кодируется так:= 1001011

разобьем такую запись на тетрады справа налево и каждую тетраду переведем в шестнадцатеричную систему (то есть, сначала в десятичную, а потом заменим все числа от 10 до 15 на буквы A, B, C, D, E, F); получаем 1001011 = 0= 4B16

Ответ: 1

7. Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв из двух бит, для некоторых – из трех): A – 000, B – 01, C – 100, D – 10, E – 011. Определить, какой набор букв закодирован строкой - ?

1) EBCEA 2) BDDEA 3) BDCEA 4) EBAEA

Решение (вариант 1, декодирование с начала):

1)  здесь используется неравномерное кодирование, при котором декодирование может быть неоднозначным, то есть, заданному коду может соответствовать несколько разных исходных сообщений;

2)  попробуем декодировать с начала цепочки, первой буквой может быть B или E, эти случаи нужно рассматривать отдельно;

3)  пусть первая буква – E с кодом 011, тогда остается цепочка

·  для кода первой буквой может быть только B с кодом 01, тогда остается ( начало исходной цепочки – EB?)

·  для кода первой буквой может быть только A с кодом 000, тогда остается 11000, а эта цепочка не может быть разложена на заданные коды букв

·  поэтому наше предположение о том, что первая буква – E, неверно

4)  пусть первая буква – B с кодом 01, тогда остается цепочка

·  для кода первой буквой может быть только D с кодом 10, тогда остается (можно полагать, что начало исходной цепочки – BD?)

·  для кода первой буквой может быть только С с кодом 100, тогда остается 011000 (начало исходной цепочки – BDC?)

Несмотря на то, что среди ответов есть единственная цепочка, которая начинается с BDC, здесь нельзя останавливаться, потому что «хвост» цепочки может «не сойтись»

·  для кода 011000 на первом месте может быть B (код 01) или E (011); в первом случае «хвост» 1000 нельзя разбить на заданные коды букв, а во втором – остается код 000 (буква А), поэтому исходная цепочка может быть декодирована как BDCEA

Ответ: 3

Решение (вариант 2, декодирование с конца):

1)  для кода последней буквой может быть только А (код 000), тогда остается цепочка

2)  для последней может быть только буква E (011), тогда остается цепочка 0110100

3)  для 0110100 последней может быть только буква C (100), тогда остается цепочка 0110

4)  для 0110 последней может быть только буква D (10), тогда остается 01 – это код буквы B

5)  таким образом, получилась цепочка BDCEA

Ответ: 3

Решение (вариант 3, кодирование ответов):

1)  в данном случае самое простое и надежное – просто закодировать все ответы, используя приведенную таблицу кодов, а затем сравнить результаты с заданной цепочкой

2)  получим

1) EBCEA – BDDEA –

3) BDCEA – EBAEA –

3)  сравнивая эти цепочки с заданной, находим, что правильный ответ – 3.

Ответ: 3

8. Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность ). Определите, какое число передавалось по каналу в виде ?

1) 5902

Решение:

1)  сначала разберемся, как закодированы числа в примере; очевидно, что используется код равномерной длины; поскольку 2 знака кодируются 10 двоичными разрядами (битами), на каждую цифру отводится 5 бит, то есть 2 → 00101 и 3 → 00110

2)  как следует из условия, четыре первых бита в каждой последовательности – это двоичный код цифры, а пятый бит (бит четности) используется для проверки и рассчитывается как «сумма по модулю два», то есть остаток от деления суммы битов на 2; тогда:

2 = 00102, бит четности (0 + 0 + 1 + 0) mod 2 = 1

3 = 00112, бит четности (0 + 0 + 1 + 1) mod 2 = 0

3)  но бит четности нам совсем не нужен, важно другое: пятый бит в каждой пятерке можно отбросить!

4)  разобъем заданную последовательность на группы по 5 бит в каждой:

01010, 10010, 01111, 00011.

5)  отбросим пятый (последний) бит в каждой группе:

0101, 1001, 0111, 0001.

это и есть двоичные коды передаваемых чисел:

01012 = 5, 10012 = 9, 01112 = 7, 00012 = 1.

6)  таким образом, были переданы числа 5, 9, 7, 1 или число 5971.

Ответ: 2

Задачи для тренировки:

1)  Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку
КОИ-8. При этом информационное сообщение уменьшилось на 800 бит. Какова длина сообщения в символах?

2)  В таблице ниже представлена часть кодовой таблицы ASCII:

Каков шестнадцатеричный код символа «p» ?

3)  Текстовый документ, состоящий из 3072 символов, хранился в 8-битной кодировке КОИ-8. Этот документ был преобразован в 16-битную кодировку Unicode. Укажите, какое дополнительное количество Кбайт потребуется для хранения документа. В ответе запишите только число.

4)  Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов ГБАВ и записать результат в шестнадцатеричной системе счисления, то получится:

1) 13D 2D16

5)  Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв - из двух бит, для некоторых - из трех). Эти коды представлены в таблице:

a b c d e

0

Определите, какой набор букв закодирован двоичной строкой

1) baade 2) badde 3) bacde 4) bacdb

6)  Для кодирования букв А, В, С, D используются трехразрядные последовательные двоичные числа, начинающиеся с 1 (от 100 до 111 соответственно). Если таким способом закодировать последовательность символов CDAB и записать результат в шестнадцатеричном коде, то получится:

1) А5СD16 4) DE516

7)  Для 6 букв латинского алфавита заданы их двоичные коды (для некоторых букв из двух бит, для некоторых – из трех). Эти коды представлены в таблице:

А В С D Е F

00 1

Определите, какая последовательность из 6 букв закодирована двоичной строкой .

1) DEFBAC 2) ABDEFC 3) DECAFB 4) EFCABD

8)  Для кодирования сообщения, состоящего только из букв А, Б, В и Г, используется неравномерный по длине двоичный код:

А Б В Г

00

Если таким способом закодировать последовательность символов ГАВБВГ и записать результат в шестнадцатеричном коде, то получится:

1) 62DD2) 6213316

9)  Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный по длине код: A=1, Б=01, В=001. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?

1) 0

10)  Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность ). Определите, какое число передавалось по каналу в виде ?

1) 662

11)  Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–10, Б–11, В–000, Г–001, Д–011. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.

1) это невозможно 2) для буквы Б – 1

3) для буквы Г –для буквы Д – 01

12)  Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код: А–111, Б–110, В–100, Г–101. Укажите, каким кодовым словом может быть закодирована буква Д. Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.

14) 000

13)  Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный по длине код: A=1, Б=000, В=001. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?

1)4) 010

Кодирование графической информации

Преобразование графической информации из аналоговой формы в дискретную производится путем дискретизации, т. е. разбиения непрерывного графического изображения на отдельные элементы. В процессе дискретизации производится кодирование, т. е. присвоение каждому элементу конкретного значения в форме кода.

Дискретизация – это преобразование непрерывного изображения в набор дискретных значений в форме кода.

В процессе кодирования изображения производится пространственная дискретизация. Пространственную дискретизацию изображения можно сравнить с построением изображения из мозаики. Изображение разбивается на отдельные мелкие фрагменты (точки), каждому из которых присваивается код цвета.

В результате пространственной дискретизации графическая информация представляется в виде растрового изображения. Растровое изображение состоит из определённого количества строк, каждая из которых содержит определённое количество точек (пиксел).

Качество изображения зависит от разрешающей способности.

Разрешающая способность растрового изображения определяется количеством точек по горизонтали (X) и количеством точек по вертикали (Y) на единицу длины изображения.

Чем меньше размер точки, тем больше разрешающая способность (больше строк растра и точек в строке) и, соответственно, выше качество изображения.
Величина разрешающей способности выражается в (dot per inch - точек на дюйм), т. е. в количестве точек в полоске изображения длиной в 1 дюйм ( 1дюйм = 2,54 см). Оцифровка графических изображений с бумаги или плёнок производится с помощью сканера. Сканирование производится путём перемещения светочувствительных элементов вдоль изображения. Характеристики сканера выражаются двумя числами, например 1200х2400 dpi. Первое число определяет количество светочувствительных элементов на одном дюйме полоски и является оптическим разрешением. Второе - является аппаратным разрешением и определяет количество микрошагов при перемещении на один дюйм вдоль изображения.

В процессе дискретизации могут использоваться различные палитр цветов. Каждый цвет можно рассматривать как возможное состояние точки. Количество цветов N в палитре и количество информации для кодирования цвета каждой точки связаны между собой известной формулой Хартли: N=2I, где I – глубина цвета, а N – количество цветов (палитра).

Количество информации, которое используется для кодирования цвета точки изображения, называется глубиной цвета. Наиболее распространёнными значениями глубины цвета являются значения из таблицы:

Таблица. Глубина цвета и количество отображаемых цветов.

Качество изображения на экране монитора зависит от величины пространственного разрешения и глубины цвета. Пространственное разрешение экрана монитора определяется как произведение количества строк изображения на количество точек в строке. Разрешение может быть: 800х600, 1024х768, 1152х864 и выше. Количество отображаемых цветов может изменяться  от 256 цветов до более чем 16 миллионов.

Рассмотрим пример формирования на экране монитора растрового изображения, состоящего из 600 строк по 800 точек в каждой строке (всего точек) и глубиной цвета 8 битов. Двоичный код цвета всех точек хранится в видеопамяти компьютера, которая находится на видеокарте.

Периодически, с определённой частотой, коды цветов точек считываются из видеопамяти и точки отображаются на экране монитора. Частота считывания изображения влияет на стабильность изображения на экране. В современных мониторах обновление изображения происходит с частотой 75 и более раз в секунду, что обеспечивает комфортность восприятия пользователем.

Информационный объём требуемой видеопамяти можно рассчитать по формуле:

 V =I · X · Y, 

где V - информационный объём видеопамяти в битах;
X · Y - количество точек изображения (разрешение экрана);
 I - глубина цвета в битах на точку.

Например, необходимый объём видеопамяти для графического режима с разрешением 800х600 точек и глубиной цвета 24 бита равен:

V =I · X · Y= 24 х 800 х 600 =бит = 1 байт.

Цветное изображение на экране монитора формируется за счет смешивания базовых цветов: красного, зеленого и синего (палитра RGB). Для получения богатой палитры цветов базовым цветам могут быть заданы различные интенсивности. Например, при глубине цвета в 24 бита на каждый из цветов, выделяется по 8 бит, т. е. для каждого из цветов возможны N=28=256 уровней интенсивности, заданные двоичными кодами от минимального до максимального .

Таблица. Формирование некоторых цветов при глубине цвета 24 бита.

Часто цвет записывается в виде - #RRGGBB, где RR – шестнадцатеричный код красной цветовой компоненты, GG - шестнадцатеричный код зеленой цветовой компоненты, BB - шестнадцатеричный код синей цветовой компоненты. Чем больше значение компоненты, тем больше интенсивность свечения соответствующего базового цвета. 00 – отсутствие свечения, FF – максимальное свечение (FF16=25510), 8016 – среднее значение яркости. Если компонента имеет интенсивность цвета <8016 , то это даст темный оттенок, а если >=8016 , то светлый.

Например,

#FF0000 – красный цвет (красная составляющая максимальная, а остальные равны нулю)

#000000 – черный цвет (ни одна компонента не светится)

#FFFFFF – белый цвет (все составляющие максимальны и одинаковы, наиболее яркий цвет)

#404040 – темно-серый цвет (все составляющие одинаковы и значения меньше среднего значения яркости)

#8080FF – светло-синий (максимальная яркость у синий составляющей, а яркости других компонент одинаковые и равны 8016 ).

Решение задач на кодирование графической информации

1. Для хранения растрового изображения размером 32×32 пикселя отвели 512 байтов памяти. Каково максимально возможное число цветов в палитре изображения?

1) 4

Решение: При кодировании с палитрой количество бит на 1 пиксель (K) зависит от количества цветов в палитре N, они связаны формулой: 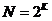(1); объем памяти на все изображение вычисляется по формуле 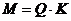(2), где – число бит на пиксель, а – общее количество пикселей.

1)  находим общее количество пикселей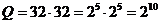

2)  находим объем памяти в битах байтбайтбитбит

3)  определяем количество бит на пиксель: 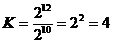бита на пиксель

4)  по таблице степеней двойки находим, что 4 бита позволяют закодировать 24 = 16 цветов

Ответ: 3

2. Для кодирования цвета фона интернет-страницы используется атрибут bgcolor="#ХХХХХХ", где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной RGB-модели.

К какому цвету будет близок цвет страницы, заданный тэгом <body bgcolor="#992299">?

1) белый 2) серый 3)желтый 4) фиолетовый

Решение: Самая высокая интенсивность цвета (99) у составляющих красного и синего цветов. Это дает фиолетовый цвет.

Ответ: 4

3. Какова ширина (в пикселях) прямоугольного 64-цветного неупакованного растрового изображения, занимающего на диске 1,5 Мбайт, если его высота вдвое меньше ширины?

1) 24

Решение: Так как объем памяти на все изображение вычисляется по формуле (1), где – число бит на пиксель, а – общее количество пикселей, которое определяется разрешением, т. е. произведением ширины на высоту изображения.

Примем ширину изображения за x, тогда Q=.

64=26 . Отсюда K=6.

Подставим эти значения в формулу (1), получим:

*6=1.5*220*23. После сокращения: x2=222. Отсюда: x=211=2048.

Ответ: 4

Задачи для тренировки:

1. Для хранения растрового изображения размером 128 x 128 пикселей отвели 4 килобайта памяти. Каково максимально возможное число цветов в палитре изображения?

1) 4

2. Для кодирования цвета фона страницы Интернет используется атрибут bgcolor="#ХХХХХХ", где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной RGB-модели. К какому цвету будет близок цвет страницы, заданной тэгом <body bgcolor="#FF8080">?

1) желтый 2) розовый 3) светло-зеленый 4) светло-синий

3. Какова ширина (в пикселях) прямоугольного 16-цветного неупакованного растрового изображения, занимающего на диске 1 Мбайт, если его высота вдвое больше ширины?

1) 24

Кодирование звуковой информации

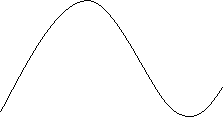
Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче, чем больше частота, тем выше тон. Для того, чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).

В процессе кодирования непрерывного звукового сигнала производится его временная дискретизация. При этом звуковая волна разбивается на мелкие временные участки, для каждого из которых устанавливается значение амплитуды.

Временная дискретизация – процесс, при котором, во время кодирования непрерывного звукового сигнала, звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина амплитуды. Чем больше амплитуда сигнала, тем громче звук.

На графике (см. рис.) это выглядит как замена гладкой кривой на последовательность ”ступенек”, каждой из которых присваивается значение уровня громкости. Чем большее количество уровней громкости будет выделено в процессе кодирования, тем более качественным будет звучание.

Рис. Временная дискретизация звука

Глубина звука (глубина кодирования) - количество бит на кодировку звука.

Уровни громкости (уровни сигнала) - звук может иметь различные уровни громкости. Количество различных уровней громкости рассчитываем по формуле Хартли: N= 2I где I – глубина звука, а N – уровни громкости.

Современные звуковые карты обеспечивают 16-битную глубину кодировки звука. Количество различных уровней сигнала можно рассчитать по формуле: N=216=65536. Т. о., современные звуковые карты обеспечивают кодирование 65536 уровней сигнала. Каждому значению амплитуды присваивается 16-ти битный код.

При двоичном кодировании непрерывного звукового сигнала он заменяется последовательностью дискретных уровней сигнала. Качество кодирования зависит от количества измерений уровня сигнала в единицу времени, т. е. частотой дискретизации. Чем большее количество измерений проводится в 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования.

Частота дискретизации – количество измерений уровня входного сигнала в единицу времени (за 1 сек). Чем больше частота дискретизации, тем точнее процедура двоичного кодирования. Частота измеряется в герцах (Гц).

1 измерение за 1 секунду -1 ГЦ, 1000 измерений за 1 секунду 1 кГц.

Обозначим частоту дискретизации буквой F. Для кодировки выбирают одну из трех частот: 44,1 КГц, 22,05 КГц, 11,025 КГц.

Считается, что диапазон частот, которые слышит человек, составляет от 20 Гц до 20 кГц.

Качество двоичного кодирования звука определяется глубиной кодирования и частотой дискретизации.

Частота дискретизации аналогового звукового сигнала может принимать значения от 8 кГц до 48 кГц. При частоте 8 кГц качество дискретизованного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц – качеству звучания аудио-CD. Следует также учитывать, что возможны как моно-, так и стереорежимы.

Аудиоадаптер (звуковая плата) – устройство, преобразующее электрические колебания звуковой частоты в числовой двоичный код при вводе звука и обратно (из числового кода в электрические колебания) при воспроизведении звука.

Характеристики аудиоадаптера: частота дискретизации и разрядность регистра.

Разрядность регистра -число бит в регистре аудиоадаптера. Чем больше разрядность, тем меньше погрешность каждого отдельного преобразования величины электрического тока в число и обратно. Если разрядность равна I, то при измерении входного сигнала может быть получено 2I =N различных значений.

Размер цифрового моноаудиофайла ( A) измеряется по формуле:

A=F*T*I/8,

где F –частота дискретизации (Гц), T – время звучания или записи звука, I разрядность регистра (разрешение). По этой формуле размер измеряется в байтах.

Размер цифрового стереоаудиофайла ( A) измеряется по формуле:

A=2*F*T*I/8,

сигнал записан для двух колонок, так как раздельно кодируются левый и правый каналы звучания.

Пример. Попробуем оценить информационный объем стереоаудиофайла длительностью звучания 1 секунда при высоком качестве звука (16 бит, 48 кГц). Для этого количество битов нужно умножить на количество выборок в 1 секунду и умножить на 2 (стерео):

16 бит*48 000 *2 = 1 536 000 бит = 192 000 байт = 187,5 Кбайт

В таблице1 показано, сколько Мб будет занимать закодированная одна минута звуковой информации при разной частоте дискретизации:

Примеры задач:

1. Определить размер (в байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при частоте дискретизации 22,05 кГц и разрешении 8 бит. Файл сжатию не подвержен.

Решение:

Формула для расчета размера (в байтах) цифрового аудио-файла: A=F*T*I/8.

Для перевода в байты полученную величину надо разделить на 8 бит.

22,05 кГц =22,05 * 1000 Гц =22050 Гц

A=F*T*I/8 = 22050 х 10 х 8 / 8 = 220500 байт.

Ответ: 220500

2. В распоряжении пользователя имеется память объемом 2,6 Мб. Необходимо записать цифровой аудиофайл с длительностью звучания 1 минута. Какой должна быть частота дискретизации и разрядность?

Решение:

Формула для расчета частоты дискретизации и разрядности: F* I =А/Т

(объем памяти в байтах) : (время звучания в секундах):

2, 6 Мбайт= 26 байт

F* I =А/Т= 26 байт: 60 = 45438,3 байт

F=45438,3 байт : I

Разрядность адаптера может быть 8 или 16 бит. (1 байт или 2 байта). Поэтому частота дискретизации может быть либо 45438,3 Гц = 45,4 кГц ≈ 44,1 кГц –стандартная характерная частота дискретизации, либо 22719,15 Гц = 22,7 кГц ≈ 22,05 кГц - стандартная характерная частота дискретизации

Ответ:

3. Объем свободной памяти на диске — 5,25 Мб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 22,05 кГц?

Решение:

Формула для расчета длительности звучания: T=A/F/I

(объем памяти в байтах) : (частота дискретизации в Гц) : (разрядность звуковой платы в байтах):

5,25 Мбайт = 5505024 байт

5505024 байт: 22050 Гц : 2 байта = 124,8 сек
Ответ: 124,8

4. Вычислить, сколько байт информации занимает на компакт-диске одна секунда стереозаписи (частота 44032 Гц, 16 бит на значение). Сколько занимает одна минута? Какова максимальная емкость диска (считая максимальную длительность равной 80 минутам)?

Решение:

Формула для расчета объема памяти A=F*T*I:
(время записи в секундах) * (разрядность звуковой платы в байтах) * (частота дискретизации). 16 бит -2 байта.
1) 1с х 2 х 44032 Гц = 88064 байт (1 секунда стереозаписи на компакт-диске)
2) 60с х 2 х 44032 Гц = 5283840 байт (1 минута стереозаписи на компакт-диске)
3) 4800с х 2 х 44032 Гц = байт=412800 Кбайт=403,125 Мбайт (80 минут)

Ответ: 88064 байт (1 секунда), 5283840 байт (1 минута), 403,125 Мбайт (80 минут)

Задачи для тренировки:

1)  Производится одноканальная (моно) звукозапись с частотой дискретизации 22 кГц и глубиной кодирования 16 бит. Запись длится 2 минуты, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1 10

2)  Производится двухканальная (стерео) звукозапись с частотой дискретизации 48 кГц и глубиной кодирования 24 бита. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 0,332

3)  Проводилась одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. В результате был получен файл размером 3 Мбайт, сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к времени, в течение которого проводилась запись?

1) 30 сексексексек

4)  Производится одноканальная (моно) звукозапись с частотой дискретизации 128 Гц. При записи использовались 64 уровня дискретизации. Запись длится 6 минут 24 секунд, её результаты записываются в файл, причём каждый сигнал кодируется минимально возможным и одинаковым количеством битов. Какое из приведённых ниже чисел наиболее близко к размеру полученного файла, выраженному в килобайтах?

1)

5) Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 32 бит. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1)4) 90