Рис. 5. Алгоритм исследования характеристик ЭСМО

2.  Цель работы

Нахождение экспериментальной зависимости T(l, m0) для элементарной системы массового обслуживания с бесконечным буфером.

3.  Порядок выполнения работы

1.  Выбрать вариант задания из таблицы 6.

2.  В соответствии с вариантом составить и отладить моделирующую программу.

3.  Провести моделирование для тестового примера. Отладить программу на тестовом примере. Подобрать объем моделирования N так, чтобы относительная погрешность экспериментальных данных для тестового примера не превосходила 10%;

4.  Провести моделирование для получения требуемой экспериментальной зависимости при 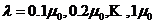. Полученные данные внести в таблицу 5.

Таблица 5 – Зависимость среднего времени пребывания запроса от интенсивности входного потока

4.  Варианты заданий

Таблица 6 – Варианты заданий к лабораторной работе №4

Для равномерного закона распределения вероятностей границы интервала значений случайной величины выбрать так, чтобы длина интервала равнялась 0.1m0.

5. Содержание отчета

1. Цель работы.

2. Формулы и графики законов распределения вероятностей для интервалов между заявками и времени обслуживания заявок.

5.  Описание разработанной программы: список использованных переменных, список использованных функций, блок-схема, листинг.

6.  Теоретический и экспериментальный графики зависимости среднего времени пребывания заявки в системе от интенсивности входного потока для тестового примера.

7.  Данные таблицы 5 и построенный по ним график.

8.  Выводы.

6.  Вопросы для самопроверки

1.  Назовите основные элементы СМО и их характеристики.

2.  Как оценивается КПД для системы массового обслуживания?

3.  Как связаны средняя длина очереди и среднее время пребывания заявки в очереди?

4.  Как связаны средняя длина очереди и среднее число заявок в СМО?

5.  Как связаны среднее время пребывания заявок в СМО и среднее число заявок в СМО?

6.  Приведите формулу для среднего времени пребывания заявки в системе, когда входной поток заявок – пуассоновский а поток обслуживания – рекуррентный.

7.  Список рекомендованной литературы

1.  Вентцель вероятности. М.: Наука. 1969 г.

2.  , , Имитационное моделирование. М.: Издательство МГТУ им. Баумана, 2008 г.

3.  Плакс моделирование систем массового обслуживания. СПб.: Издательство СПбГААП, 1995.

Лабораторная работа № 5.

Моделирование элементарной СМО с конечным буфером

1.  Необходимые теоретические сведения

Для СМО с конечным буфером размер буфера N влияет на все основные характеристики функционирования СМО. В такой системе средняя задержка всегда ограничена, т. к. средняя длина очереди запросов ограничена сверху величиной N . С другой стороны, когда буфер заполнен, поступление очередного запроса на вход СМО приводит к потере либо этого запроса, либо какого-то запроса из буфера. Поэтому даже при < производительность системы Q < . Справедливо выражение

где Pотк - вероятность потери запроса из-за переполнения буфера. Величина Pотк максимальна при N = 0 и стремится к нулю при неограниченном увеличении N. Рассчитать эту зависимость в общем случае довольно сложно. В частном случае для ЭСМО с пуассоновским входным потоком и экспоненциально распределенным временем обслуживания зависимость имеет вид

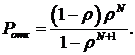
Очевидно, что и в общем случае вероятность отказа уменьшается к нулю при увеличении объема буфера. Среднее время отклика системы на запрос с увеличением объема буфера возрастает. Это объясняется тем, что сокращение объема буфера приводит к укорочению средней длины очереди запросов за счет того, что увеличивается доля запросов, получающих отказ в обслуживании. В общем случае зависимость Lсист от N является сложной.

Приведенные зависимости основных характеристик ЭСМО от N обычно используются для отладки логики моделирующей программы.

2.  Рекомендации по моделированию СМО

Алгоритм, моделирования работы СМО с буфером объема N , отличается от алгоритма на рис. 5 лишь небольшой модификацией. Перед увеличением значения m (числа заявок в буфере) необходимо сравнить его с N и при m=N пропустить операции увеличения m и формирования случайного числа tз. Это будет соответствовать отказу в обслуживании поступившей заявке, когда буфер заполнен.

3.  Цель работы

Нахождение экспериментальных зависимосте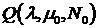й и 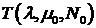для элементарной системы массового обслуживания с буфером объема N.

4. Порядок выполнения работы

1. Выбрать вариант задания из таблицы 8.

2. В соответствии с вариантом составить и отладить моделирующую программу.

3. Провести моделирование для тестового примера. Отладить программу на тестовом примере. Подобрать объем моделирования M так, чтобы относительная погрешность экспериментальных данных для тестового примера не превосходила 10%.

4. Провести моделирование для получения требуемых экспериментальных зависимостей при . Полученные данные занести в таблицу 7.

Таблица 7 – Зависимость среднего времени пребывания запроса в системе и производительности системы от интенсивности входного потока

5. Варианты заданий

Таблица 8 – Варианты заданий к лабораторной работе №5

Для равномерного закона распределения вероятностей границы интервала значений случайной величины выбрать так, чтобы длина интервала равнялась .

6. Содержание отчета

1. Цель работы.

2. Формулы и графики законов распределения вероятностей интервалов между заявками и времени обслуживания заявок.

3. Описание разработанной программы: список использованных переменных, список использованных функций, блок-схема, листинг.

4. Теоретический и экспериментальный графики зависимостей производительности СМО и среднего времени задержки запроса от интенсивности входного потока для тестового примера.

5. Экспериментальные графики зависимостей производительности СМО и среднего времени задержки запроса в СМО от интенсивности входного потока для своего варианта.

6.  Выводы.

7.  Вопросы для самопроверки

1.  Назовите основные элементы СМО и их характеристики.

2.  Как оценивается КПД для системы массового обслуживания?

3.  Как связаны средняя длина очереди и среднее время пребывания заявки в очереди?

4.  Как связаны средняя длина очереди и среднее число заявок в СМО?

5.  Как связаны среднее время пребывания заявок в СМО и среднее число заявок в СМО?

6.  Приведите верхнюю оценку для среднего времени пребывания заявки в системе, когда входной поток заявок – пуассоновский а поток обслуживания – рекуррентный.

8. Список рекомендованной литературы

1. Вентцель вероятности. М.: Наука. 1969 г.

2. , , Имитационное моделирование. М.: Издательство МГТУ им. Баумана, 2008 г.

3. Плакс моделирование систем массового обслуживания. СПб.: Издательство СПбГААП, 1995.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4