Важнейшим частным случаем рекуррентного потока является так называемый пуассоновский поток, для которого плотность распределения вероятностей fu(x) задается формулой экспоненциального распределения:
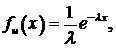
где l – интенсивность пуассоновского потока. Для пуассоновского потока su = mu, и, следовательно, vu = 1, т. е. по уровню случайности пуассоновский поток можно считать антиподом к детерминированному потоку. Пуассоновский поток достаточно хорошо аппроксимирует большинство потоков, встречающихся в социальных и технических систем (например, интервалы времени между приходящими к врачу пациентами или встающими в очередь покупателями в магазине)
В ряде практических приложений входной поток заявок является эрланговским. Эрланговские потоки по уровню случайности являются промежуточными между детерминированными и пуассоновскими. Эрланговский поток порядка k получается из пуассоновского потока, в котором оставляется лишь каждый k-ая заявка, а остальные выбрасываются. Такая операция называется прореживанием потока. Примером подобного потока является поток проходящих через турникет метрополитена людей. Исходный поток людей, входящих в вестибюль метро, является пуассоновским и делится примерно поровну между всеми N турникетами.
Функция fu(x) для эрланговского потока порядка k > 1 в общем виде вычисляется довольно сложно, но коэффициент вариации найти несложно. Можно показать, что для эрланговского потока , т. е. с увеличением k vu убывает к нулю.
Стохастические нестационарные потоки заявок.
В реальных системах интенсивность потока запросов редко бывает строго постоянной. Например, интенсивность потока покупателей в течение суток может изменяться в несколько раз. Это явление отражено в понятиях «часы максимальной нагрузки» и «часы минимальной нагрузки». В большинстве случаев можно считать, что нестационарность потока обусловлена только тем, что его интенсивность изменяется во времени.
Однородные и неоднородные потоки заявок.
Различие между однородными и неоднородными потоками заключается в том, что в однородных потоках все заявки имеют равный приоритет на обслуживание в ОУ, в то время как в неоднородном потоке приоритеты могут различаться. Например, во многих социальных организациях висят объявления о том, что граждане, принадлежащие к льготным категориям, обслуживаются вне очереди.
Распространенной причиной неоднородности потока заявок является то, что в заявках содержится информация, которая учитывается при обслуживании запроса в буфере и в ОУ, и от которой, следовательно, зависят характеристики этого обслуживания. Так, например, в системах сбора данных, где заявками являются приходящие сообщения, такой информацией является время создания сообщения, и чем более актуально сообщение, тем скорее оно должно быть обработано.
1.3 Моделирование входного потока заявок
Современные вычислительные средства обладают высокой производительностью. Умение пользоваться их ресурсами позволяет нивелировать недостатки имитационного моделирования по сравнению с классическими методами анализа. За одну секунду реального времени можно промоделировать работу системы в течение нескольких часов. В настоящее время при имитационном моделировании СМО, как правило, применяется подход, называемый «моделирование по событиям». Кратко опишем ключевые особенности такого подхода.
Состояние системы описывается набором из нескольких переменных (например, количество заявок в очереди, занятость ОУ и т. д.). Также вводится переменная, хранящая системное время. Характерной чертой СМО является то, что состояние системы остается постоянным в интервале между двумя соседними произошедшими событиями. Моменты времени, в которые происходит смена состояния системы, называются особыми. Таким образом, можно имитировать систему только в особые моменты времени. При этом, системное время будет изменяться скачкообразно – от момента к моменту.
Воспользуемся описанным подходом для построения имитационной модели, с помощью которой необходимо оценить интенсивность входного потока. Введем следующие переменные:
· N – количество поступивших заявок;
· tc - текущее системное время.
При анализе только входного потока заявок имеется три вида особых моментов: начало времени моделирования (tc = 0), момент прихода заявки и момент окончания моделирования. Моделирование должно осуществляться до тех пор, пока не поступит заданное число заявок N. Предположим, для этого потребовалось T единиц системного времени. Тогда оценку интенсивности можно вычислить по формуле:
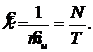
Для оценки коэффициента вариации помимо математического ожидания mu необходимо знать также среднеквадратическое отклонение su. Для оценки su можно воспользоваться формулой для нахождения выборочной дисперсии:
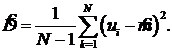
где ui - значение i-го интервала между заявками. Тогда ![]() , а
, а 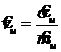 .
.
Величина N выбирается, исходя из требуемой точности оценивания. Как было сказано выше, для интервалов между заявками максимальное значение коэффициента вариации равно единице и среднеквадратическое отклонение не может быть больше математического ожидания: smax = mu (в противном случае, существует ненулевая вероятность того, что интервал между заявками будет отрицательным, что физически невозможно). Тогда при оценке математического ожидания длительности интервала по одному измерению среднеквадратическое значение ошибки не больше smax = mu. При оценке по выборке объема N среднеквадратическая ошибка не больше, чем ![]() (см. лабораторную работу №1). Тогда относительная среднеквадратическая ошибка оценки средней длительности интервала между заявками не больше
(см. лабораторную работу №1). Тогда относительная среднеквадратическая ошибка оценки средней длительности интервала между заявками не больше 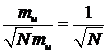 . На основании этих рассуждений можно предложить инженерное правило, позволяющее выбрать объем выборки, достаточный для обеспечения ошибки оценивания не более 1%. Начальное значение объема выборки выбирается равным 10000. Производится оценка интенсивности и коэффициента вариации. Затем объем выборки удваивается и снова проводится оценка. Если оценка изменились не более чем на 1%, то считается, что требуемая точность достигнута. Если нет, то объем выборки снова удваивается и т. д. Стоит отметить, что данный способ можно использовать только когда оцениваемые параметры заведомо отличны от нуля.
. На основании этих рассуждений можно предложить инженерное правило, позволяющее выбрать объем выборки, достаточный для обеспечения ошибки оценивания не более 1%. Начальное значение объема выборки выбирается равным 10000. Производится оценка интенсивности и коэффициента вариации. Затем объем выборки удваивается и снова проводится оценка. Если оценка изменились не более чем на 1%, то считается, что требуемая точность достигнута. Если нет, то объем выборки снова удваивается и т. д. Стоит отметить, что данный способ можно использовать только когда оцениваемые параметры заведомо отличны от нуля.
С учетом всего вышесказанного, представим алгоритм моделирования.
1. Начальные условия tс = 0, N = 10000, k = 0, ![]() ,
, ![]() .
.
2. k = k + 1.
3. Формировать случайное число uk, распределенное по заданному закону fu(x).
4. tс = tс + uk.
5. Если k < N, то переход в пункт 2.
6. 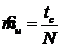 .
.
7. 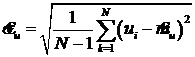 .
.
8. 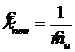 .
.
9. 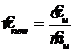 .
.
10. Если 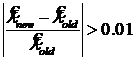 или
или 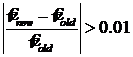 , то
, то 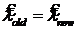 ,
, 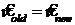 , tс = 0, k = 0, N = 2N и переход к пункту 2.
, tс = 0, k = 0, N = 2N и переход к пункту 2.
11. 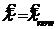 ,
, 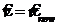 .
.
2. Цель работы
Исследование основных характеристик входных потоков заявок, а также базовых принципов моделирования СМО по событиям.
3. Порядок выполнения работы
1. Выбрать из таблицы 4 в соответствии с вариантом закон распределения интервалов между двумя соседними заявками.
2. Рассчитать теоретическое значение интенсивности l и вариации vu.
3. Написать программу, реализующую методику оценки интенсивности потока, описанную в п. 1.3 .
4. При помощи программы произвести оценку интенсивности и коэффициента вариации заданного потока;
5. Построить график зависимости оценок ![]() и
и ![]() от величины N.
от величины N.
4. Варианты заданий
Таблица 4 – Варианты заданий к лабораторной работе №2
Номер варианта | Порядок эрланговского потока | Параметр l |
1 | 1 | 1 |
2 | 2 | 2 |
3 | 3 | 3 |
4 | 4 | 4 |
5 | 1 | 5 |
6 | 2 | 6 |
7 | 3 | 7 |
8 | 4 | 8 |
9 | 1 | 9 |
10 | 2 | 10 |
11 | 3 | 11 |
12 | 4 | 12 |
13 | 1 | 13 |
14 | 2 | 14 |
15 | 3 | 15 |
16 | 4 | 16 |
17 | 1 | 17 |
18 | 2 | 18 |
19 | 3 | 19 |
20 | 4 | 20 |
21 | 1 | 21 |
22 | 2 | 22 |
23 | 3 | 23 |
24 | 4 | 24 |
25 | 5 | 25 |
5. Содержание отчета
1. Цель работы.
2. Формула и график закона распределения интервалов.
3. Описание разработанной программы: список использованных переменных, список использованных функций, блок-схема, листинг.
4. Графики зависимости оценок интенсивности и коэффициента вариации от M. На графиках уровнем отметить теоретические значения эти величин;
5. Выводы.
6. Вопросы для самопроверки
1. В чем отличие детерминированных потоков от стохастических? Приведите примеры.
2. Приведите характеристики потоков событий.
3. Что такое стационарные и нестационарные стохастические потоки? Приведите примеры.
4. Что такое рекуррентные и нерекуррентные потоки?
5. В чем заключается свойство рекуррентности потока?
6. Как экспериментально вычисляется оценка интенсивности потока?
7. Как экспериментально проверить отсутствие последействия в потоке?
8. Как проверяется гипотеза о нестационарности потока?
7. Список рекомендованной литературы
1. Вентцель вероятности. М.: Наука. 1969 г.
2. , , Имитационное моделирование. М.: Издательство МГТУ им. Баумана, 2008 г.
3. Плакс моделирование систем массового обслуживания. СПб.: Издательство СПбГААП, 1995.
Лабораторная работа № 4.
Моделирование элементарной СМО с бесконечным буфером
1. Необходимые теоретические сведения
1.1 Введение
К системам массового обслуживания (СМО) можно отнести любую систему, способную выполнять некоторые запросы, поступающие извне. Примером может служить обслуживание покупателей продавцом, прохождение посетителей метрополитена через турникет, обработка центральным процессором запросов пользователя компьютера и т. д. Таким образом, источником запросов (ИЗ) может быть и явление природы, и технический объект. Часть системы, непосредственно выполняющую запрос, принято называть обслуживающим устройством (ОУ).
Одной из характерных черт СМО является то, что запросы, которые не могут быть обслужены немедленно (из-за занятости ОУ), могут быть помещены в очередь на обслуживание. По этой причине СМО часто называют системами с очередями. Место, отводимое для очереди запросов, в теории СМО называют буфером. Типичный пример буфера – приемная перед кабинетом начальника.
В простейшем случае СМО состоит только из одного ОУ. Но в этой системе отсутствуют очереди запросов и для приложений она не очень интересна. Поэтому в качестве элементарной СМО (ЭСМО) будем рассматривать СМО, содержащую одно ОУ и один буфер.
Основные модели входного потока заявок были рассмотрены в предыдущей лабораторной работе. Остановимся подробней на моделях буфера и обслуживающего устройства.
1.2 Модель буфера
Буфер, как правило, характеризуется объемом, определяющим максимальное количество запросов, которые могут помещаться в очередь, а также правилом обслуживания очереди. Это правило позволяет указать, какой запрос из очереди поступает для обслуживания на освободившееся ОУ.
По объему буферы делятся на конечные и бесконечные. Частным случаем конечного буфера является буфер объема 0, что в действительности соответствует отсутствию буфера.
При поступлении запроса на вход заполненного буфера возможны 2 варианта действий: либо поступивший запрос получит отказ в обслуживании и не будет впущен в СМО, либо из буфера будет удален другой запрос, а на его место будет помещен поступивший. Во втором случае должен быть сформулирован алгоритм, позволяющий однозначно определять удаляемый запрос. Возможны случаи, когда запрос удаляется из буфера без каких-либо внешних факторов просто потому, что он потерял актуальность. Например, очередь в железнодорожную кассу может значительно уменьшиться после отхода очередного поезда. В подобных случаях бывает целесообразно для таких «нетерпеливых» запросов устанавливать повышенный приоритет, чтобы ускорить их обслуживание.
Порядок обслуживания запросов, находящихся в буфере, может значительно влиять на характеристики работы СМО. Как правило, используется одно из следующих правил.
1). Информация о запросах игнорируется, а выбор следующего обрабатываемого запроса осуществляется на основе равновероятного распределения.
2). Руководящей информацией является время поступления запроса. Тогда выбирается либо запрос, поступивший ранее остальных (правило FIFO: first in – first out, первым пришел - первым вышел), либо запрос, поступивший последним (правило LIFO: last in – first out, последним пришел - первым вышел).
3). Выбор осуществляется, исходя из приоритета запросов. В ОУ поступает запрос с наибольшим приоритетом.
4). Если для каждого запроса известно время его выполнения, то можно выбирать либо запрос с минимальным, либо запрос с максимальным временем выполнения.
5). Если для каждого запроса известно предельное время его жизни в СМО (время, после которого его выполнение уже не актуально), то можно выбирать запрос, которому жить осталось меньше, чем другим.
Каждое из сформулированных правил выбора запроса из буфера может в зависимости от ситуации оказаться оптимальным с точки зрения повышения производительности СМО или улучшения других ее характеристик.
1.3 Модель обслуживающего устройства
Чтобы описать модель ОУ, необходимо для поступающих запросов задать трудоемкости их выполнения. Если производительность ОУ одинакова для всех запросов, то задание трудоемкости выполнения запроса эквивалентно заданию времени выполнения запроса. В ряде случаев время выполнения запроса может быть вычислено или оценено на основе информации, содержащейся в самом запросе.
Времена выполнения (обслуживания) запросов могут быть либо одинаковыми (в простейшем случае), либо разными, но фиксированными, либо случайными. В последнем случае для их задания могут применяться распределения вероятностей. Пусть s1,s2,… - случайные времена обслуживания запросов, которые попарно статистически независимы и все имеют одну и ту же плотность распределения вероятностей gs(x). Интенсивностью обслуживания называется величина ![]() , где
, где ![]() - математическое ожидание случайной величины s. Интенсивность обслуживания m равна среднему числу обслуживаемых запросов на промежутке времени, выбранном за единицу (1сек., 1мин., 1час и т. д.). Для характеристики случайного обслуживания также важную роль играет коэффициент вариации
- математическое ожидание случайной величины s. Интенсивность обслуживания m равна среднему числу обслуживаемых запросов на промежутке времени, выбранном за единицу (1сек., 1мин., 1час и т. д.). Для характеристики случайного обслуживания также важную роль играет коэффициент вариации ![]() , равный отношению среднеквадратического значения к среднему значению случайной величины s.
, равный отношению среднеквадратического значения к среднему значению случайной величины s.
Если поток запросов неоднороден, и складывается из однородных потоков с разными приоритетами, то для каждого однородного подпотока может быть задано свое распределение вероятностей времени обслуживания. При наличии разноприоритетных запросов необходимо указать правило, которым руководствуется ОУ, когда во время обслуживания низкоприоритетного запроса, поступает высокоприоритетный запрос. Возможны следующие варианты:
· обслуживание низкоприоритетного запроса прекращается; в этом случае говорят о том, что приоритеты абсолютны;
· обслуживание низкоприоритетного запроса не прекращается; в этом случае говорят о том, что приоритеты относительны.
В случае прерывания обслуживания необходимо оговорить, возвращать ли недообслуженный запрос в буфер для дальнейшего дообслуживания или отказывать ему в обслуживании и удалить из СМО.
1.4 Основные характеристики ЭСМО
Для оценки эффективности работы СМО используется ряд характеристик. При этом интересы владельца СМО и ее пользователя могут не совпадать. В частности, для владельца важны такие характеристики как производительность системы и ее стоимость, в то время как для пользователя представляют интерес оперативность системы и вероятность отказа в обслуживании.
Производительность системы Q равна среднему числу запросов, обслуживаемых системой в единицу времени. Производительность СМО не может быть больше интенсивности входного потока запросов l, так как не может быть обслужено больше запросов, чем их поступило в СМО. Кроме того, производительность СМО не превосходит интенсивности обслуживания m, так как в предельном случае, когда сервер работает без простоев, его производительность m как раз и определяет производительность СМО. Таким образом, верна оценка
![]()
С точки зрения эксплуатации системы важной характеристикой является коэффициент загрузки системы
![]()
который показывает, насколько эффективно используется система, т. е. какую долю времени система действительно обрабатывает запросы, а не простаивает.
Для системы с бесконечным буфером все заявки поступают в буфер и в конечном итоге обслуживаются, поэтому вероятность отказа в обслуживании для такой системы равна нулю.
Оперативность СМО (т. е. время ее реакции на запрос) обычно характеризуют средним значением времени пребывания запроса в системе. Это время T складывается в общем случае из времени ожидания запроса в буфере и времени обработки запроса в сервере. Среднее время пребывания запроса в системе связано со средним числом запросов в системе Lсист простой формулой, известной как теорема Литтла:
![]()
Если входной поток запросов является пуассоновским, то для вычисления T можно воспользоваться формулой Поллачека–Хинчина:
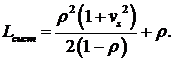
Стоимость ЭСМО в простейшем случае представляется в виде суммы стоимостей буфера и сервера, причем, стоимость буфера считается линейной функцией от объема буфера N, а стоимость сервера считается линейной функцией от его производительности m. Тогда формула для стоимости СМО имеет вид:
![]()
где Aбуф и Aсерв - некоторые коэффициенты. Отметим, что на практике зависимость Cсмо от аргументов может быть более сложной, но в любом случае она должна оставаться монотонно не убывающей от величин m и N.
1.5 Рекомендации по моделированию СМО
Для увеличения скорости моделирования СМО целесообразно использовать, подход, называющийся «моделированием по событиям». Основные принципы этого подхода были изложены во вводной части к третьей лабораторной работе. Итак, в ЭСМО присутствуют следующие особые события: поступление заявки в СМО, прием заявки на обслуживание, окончание обслуживания заявки.
Тогда состояние СМО будет описываться следующим набором переменных:
1. tс - системное время.
2. zan – переменная, равная единице, если ОУ занят, и нулю, если ОУ свободен.
3. tз - следующий момент поступления заявки.
4. tосв - следующий момент освобождения ОУ.
5. n – количество заявок, поступивших к данному моменту в СМО.
6. k – количество заявок, обслуженных к данному моменту в ОУ.
7. m – количество заявок в буфере.
Программа должна заданное число раз выполнить следующий перечень действий: определение момента следующего особого события, имитация события, корректировка результатов. Обобщенный алгоритм исследования различных параметров СМО представлен на рис. 5.
Существует ряд подходов к выбору условия окончания моделирования. Один из них заключается в построении гистограмм распределения входного потока заявок и времени обслуживания. Как только для гистограмм этих распределений выполнятся условия, приведенные в лабораторной работе №2, моделирование можно считать выполненным. Можно так же воспользоваться правилом, предложенным в лабораторной работе №3.
Для оценки правильности составленной модели необходимо провести тестовое испытание при пуассоновском входном потоке. Полученный результат T(l, m0) можно проверить при помощи формулы Поллачека-Хинчина.


|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |




