Применение методов интервальной арифметики к задаче построения псевдотраектрий

, аспирант факультета Мат-Мех
СПбГУ, *****@***ru

В работе описан алгоритм, поиска псевдотраекторий[1], основанный на использовании аппарата интервальных вычислений. Приводится описание некоторых технических особенностей реализации, позволивших ускорить процесс вычислений.

1. Введение

При реализации алгоритма решалась следующая задача: рассматриваются некоторая динамическая система f, точки , значение параметра k – количества шагов. Необходимо найти псевдотраектории, проходящие сначала через точку , а потом – через точку , при вычисленном, в процессе построения точной траектории, значении параметра ε, по следующей формуле , где ρ – евклидово расстояние.

Алгоритм реализован с использованием библиотеки интервальных вычислений[6]. Такой подход позволяет частично снять проблему с ошибками округления, так как мы работаем не числом, с некоторой окрестностью этого числа.

При использовании интервальной арифметики может возникнуть проблема завышения результата. Как показано в [6],этой проблемы не возникает, если интервальная функция удовлетворяет условию Липшица[6].

В реализации алгоритма, взаимодействие с динамической системой осуществляется на основе смешанных вычислений[2]. При таком подходе для исходной системы строится ее объектная аппроксимация в виде экземпляра некоторого класса, созданного динамически, хранящего основные свойства системы (размерность и границы фазового пространства, и. т. д.) и позволяющего эффективно манипулировать ими(Например, вычислять состояния системы ).

2. Интервальная арифметика

И Интервалом будем называть множество вида:

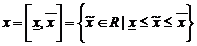
За IR обозначим пространство всех интервалов над R.

Пусть 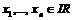. Тогда интервальным вектором будем называть

За обозначим пространство всех интервальных векторов.

Вводится операция "□" ― построения оболочки множества в R. Пусть ― непустое ограниченное множество. Тогда

□

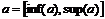
Т. е. операция "□" является операцией построения минимального интервала, содержащего множество a.

Операцию " □" можно ввести для множества из

Пусть ― непустое ограниченное множество. Тогда

□

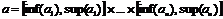
где ― проекция множества a на i-ую ось,

Обозначим через Ω множество операций, которые допустимы в интервальной арифметике.

Ω ={ +, –, ·, / }.

Определим действие операции "◦" следующим образом:

Пусть , тогда

x◦y=□{◦| }

Пусть 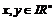, тогда

x◦y=□{[◦]×…[◦]| }

Рассмотрим множество функций Φ

Φ = { sqr, sqrt, ln, exp, sin, cos }.

Для функции можно определить ― расширение φ на интервальный вектор. Такое расширение будем называть интервальной функцией.

Пусть

=□

Таким образом, можно включить в Φ любую вещественную функцию, непрерывную на замкнутом интервале своего задания. Функция на интервальных векторах определяется аналогично[6].

3. Алгоритм построения псевдотраекторий

1.  Обозначим за m индекс, при котором указанное выше расстояние минимально. Т. е. . В случае, когда m<k количество шагов уменьшается, значение параметра m становится новым значением количества шагов.

2.  Определим, существуют ли другие псевдотраектории с таким же ε, проходящие сначала через точку , а потом – через точку . Обозначим, workingSet – множество, хранящие результаты промежуточных вычислений, полученные в процессе построения псевдотраектории.

a.  Пусть функция является расширением функции f на интервальный аргумент.

b.  Построим ε–окрестность начальной точки :

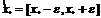
c.  Введем логический 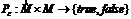, который определяется следующим образом: , если ε – окрестность точки x содержит в себе интервал I. Иначе – false.

d.  Если , тогда

e.  Если , тогда □

f.  Иначе

Если множество 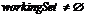. Тогда оно имеет следующий вид: .

В этом случае результатом работы алгоритма будет любая псевдотраектория E, построенная по следующему правилу:

.

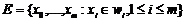Иначе считаем, что результатом работы алгоритма будет псевдотраектория, которая имеет следующий вид:

и других псевдотраекторий с таким ε нет.

4. Реализация

Алгоритм поиска псевдотраекторий реализован на языке C# Поддержка "смешанных вычислений" реализована с использованием технологий ".Net reflection", и ".Net Code Document Object Model". [7]

Визуализация результата реализована с помощью GNUPLOT технологии[8]. Пользовательский интерфейс реализован с помощью технологии ".Net Windows Forms" [7].

4.1. Пользовательский интерфейс

На сегодняшний день, графический пользовательский интерфейс(GUI) является очень важной частью большинства программ, ориентированных на взаимодействие с пользователем, потому что предоставляет возможность удобного использования всех их возможностей путем манипуляций над некоторым набором видимых экранных элементов.

В реализации алгоритм поиска псевдотраекторий используется GUI, реализованный на языке C# с помощью технологии GNUPLOT[8], предоставляеющий возможность ввода данных через специальную форму, визуализации результата работы алгоритма и сохранении графического результата на диск.

На рисунке 1. изображен результат поиска псевдотраектоий системы Хенона[1].

4.2. Смешанные вычисления

При реализации алгоритма поиска псевдотраекторий использовалась технология MCP[4], предоставляющая библиотеку, содержащую в себе средства для создания объектной аппроксимации исходной системы в виде некоторого экземпляра класса, созданного динамически, хранящего основные свойства системы (размерность и границы фазового пространства, и. т. д.) и позволяющего эффективно манипулировать ими(Например, вычислять состояния системы ). [2] При таком подходе используется описание динамической системы (ДС) на языке DSDL[4] [5], которое подается на вход специальному анализатору[5], который сначала его разбирает, а затем специальный генератор[5], по построенному дереву разбора, создает класс, реализующий интерфейс ISystem<Type>[4], Реализация созданного класса может основываться на использовании не только традиционной вещественной арифметики, но и на интервальной.

Процесс создания объектной аппроксимации исходной системы условно можно разбить на следующую последовательность действий:

1.  Представление описания ДС в виде абстрактного дерева.

2.  Дифференцирование (если правая часть системы задана дифференцируемой функцией).

3.  Генерация текста класса.

4.  Создание экземпляра класса.

5.  Сохранение данного объекта на диск в XML-формате.

Нам удобен способ сохранения объектной аппроксимации исходной ДС в XML-формате по следующим причинам:

1.  Обеспечение совместимости программных комплексов, при совестном использовании ОА исходной ДС.

2.  Возможность использования валидации ОА исходной ДС, перед повторным использованием.

3.  Возможность использования XSLT-трансформации в некоторую XML-структуру, традиционно используемую другими программными средствами при решении схожих задач.

4.3. Вычисление константы Липшица

Константа Липшица используется для оценки роста функции и как следствие – завышении результата[6].

Пусть 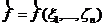- арифметическое выражение от формальных переменных

Константа Липшица вычисляется по следующей формуле:

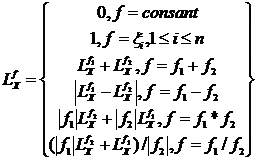, где

При вычислении нормы функции используется многопоточный распределенный алгоритм, а также объектное представление арифметических выражений, созданных динамически, позволяют ускорить процесс вычисления значения функции в некоторой точке.

Литература

1. , . Введение в символический анализ динамических систем. изд. СПбГУ, 2005.

2. . Смешанные вычисления. "В мире Науки", 14.02.1984. с..

3. , . Применение методов интервальной арифметики к задаче построения символического образа. Электронный журнал “Дифференциальные уравнения и процессы управления”,(http://www. *****/journal), номер 4, 2006.

4. Терентьев и реализация программного комплекса для компьютерного моделирования и исследования ДС. Научное программное обеспечение в образовании и научных исследованиях: Труды научно-технической конференции. Спб. Изд. Политех. Ун-та, 20с.

5. А. Ахо, Р. Сети, Дж. Ульман. Компиляторы: принципы, технологии, инструменты. — М., Издательский дом "Вильямс", 2003. —768 с.

6. Neumaier A., Interval Methods for systems of equations, Cambridge University Press 1990.

7. MSDN (http://msdn. /library/).

8. GNUPLOT (http://gnuplot. /).