Дюрация и показатель выпуклости облигации

Дюрация и показатель выпуклости облигации

Основной фактор риска на рынках инструментов с фиксированными доходами, не имеющих кредитного риска – процентный риск.

Процентный риск – возможность изменения цены облигации вследствие изменения безрисковых процентных ставок. Цены различных облигаций по разному реагируют на изменения процентных ставок.

Чувствительность цены облигации к изменению процентных ставок, т. е. процентный риск облигации характеризуется величиной .

Оценим величину при заданном изменении процентных ставок.

Рассмотрим облигацию, по которой через t1, t2,…,tn лет от текущего момента времени t=0 выплачиваются денежные суммы С1, С2,…,Сn соответственно.

Предположим, временная структура процентных ставок такова, что безрисковые процентные ставки для всех сроков одинаковы и равны r. Тогда рыночная стоимость облигации равна

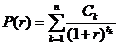
Предположим, временная структура процентных ставок мгновенно изменилась так, что безрисковые процентные ставки для всех сроков изменились на одну и ту же величину . Тогда стоимость облигации станет равной .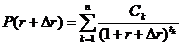

Приращение стоимости облигации в результате изменения процентных ставок равно .

Оценим величину , не производя точных вычислений. Считая достаточно малым по абсолютной величине, получим по формуле Тейлора

.

С учетом членов разложения второго порядка

.

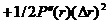Члены более высокого порядка считаются незначительными при оценке чувствительности цены облигации к изменению процентных ставок на рынке. Для относительных приращений цены облигации получаем

И

+.

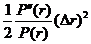Так как , то .

.

Тогда ; .

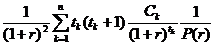Определение: число D=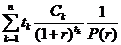 называется дюрацией облигации, или дюрацией Маколея.

Дюрация облигации представляет собой средневзвешенный срок выплат по облигации, где веса – это текущие стоимости выплат по облигации, деленные на рыночную цену облигации. Таким образом, коэффициент 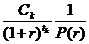выражает долю рыночной цены облигации, которая будет получена через лет, k=1,2,…,n. Сумма коэффициентов в D равна единице:

Определение: число C=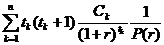 называется показателем выпуклости облигации.

Таким образом, ; .

Тогда из формул или

+.

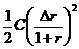Все полученные выражения верны при условии горизонтальности временной структуры процентных ставок и параллельности ее перемещений.

Т. о., дюрация облигации оценивает чувствительность цены облигации к изменению временной структуры процентных ставок: 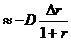. Чем больше дюрация облигации, тем больше величина по модулю, т. е., тем больше процентный риск облигации. Значит, при определенных условиях дюрацию облигации можно рассматривать как меру процентного риска облигации.

С другой стороны, из +следует, что чем больше выпуклости С, тем менее точным является приближенное равенство , значит тем хуже дюрация облигации оценивает величину . Следовательно, показатель выпуклости облигации можно рассматривать как показатель того, насколько точно дюрация облигации оценивает величину .

В момент t=0 дюрация облигации является мерой ее процентного риска при следующих условиях:

1)  в начальный момент времени безрисковые процентные ставки для всех сроков одинаковы и равны r (кривая доходностей является горизонтальной);

2)  процентные ставки для всех сроков изменились мгновенно в этот же момент на одну и ту же величину (кривая доходностей переместилась параллельно самой себе);

3)  мало;

4)  Показатель выпуклости облигации мал, т. е. справедлива формула .

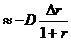Определим стоимость облигации после изменения процентных ставок P(r+) от . Из выведенных формул получим, что эта зависимость может быть

1)  Точной ,

2)  Линейной ,

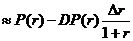3)  Квадратичной +.

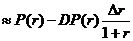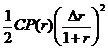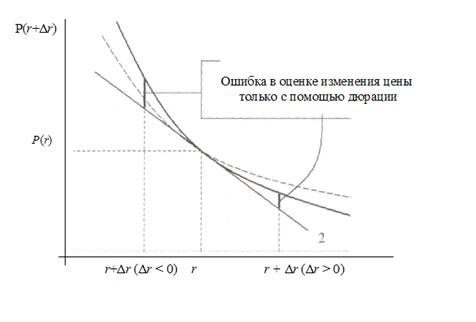
На рисунке показана зависимость стоимости облигации P(r+) от .

Кривая 1 построена для точного поведения цены, является убывающей и выпуклой. Кривая 2 определяет изменение цены только с помощью дюрации облигации и является линейной относительно . Кривая 3 определяет изменение цены облигации с помощью дюрации и показателя выпуклости, является квадратичной относительно .

Замечание. Дюрация Маколея – одно из фундаментальных понятий теории финансовых инвестиций. Как было сказано дюрация Маколея определяется при условии горизонтальности кривой доходностей
и параллельности ее сдвигов. В реальности кривая доходностей не является горизонтальной и ее сдвиги не обязательно параллельны. Однако, исследования показывают, что трудно делать прогнозы более точными, чем по модели с неизменной процентной ставкой. Введение понятия дюрации привело к развитию техники управления пакетами облигаций, которая известна под названием иммунизации.

Свойства дюрации и показателя выпуклости облигации

Рассмотрим облигацию с купонами. Безрисковые процентные ставки для всех сроков одинаковы.

Справедливы следующие утверждения:

1. Дюрация облигации не превосходит срока до ее погашения Т.

2. Дюрация чисто дисконтной облигации равна сроку до ее погашения.

3. Если облигация не является чисто дисконтной
, то чем больше внутренняя доходность облигации, тем меньше ее дюрация и показатель выпуклости.

4. Если все платежи по облигации отсрочить на t0 лет, не изменяя ее внутренней доходности r, то дюрация облигации увеличится на t0 лет, а показатель выпуклости – на (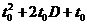) лет.

5. Если до погашения облигации
остается больше одного купонного периода, то при заданном значении внутренней доходности r дюрация облигации и показатель выпуклости тем больше, чем меньше купонная ставка.

6. Зависимость дюрации облигации от срока до погашения при неизменных g и r cформулируем в виде следующих утверждений:

6.а ;

6b Если g≥r, то последовательность {Dn} является возрастающей;

6с Если g<r, то можно указать число n0 такое, что для облигаций с числом периодов до погашения n< n0 последовательность { Dn} является возрастающей.

Докажем несколько свойств:

1.  Доказательство:

D=≤==.

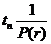
2.  Доказательство:

Покажем, что дюрация и показатель выпуклости облигации – это убывающие функции r.

Рассмотрим производную

=

Покажем, что выражение в квадратных скобках отрицательно. Имеем:

=

- - = -
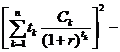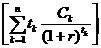
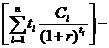
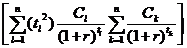