ГОУ Гимназия № 000
«Московская городская педагогическая гимназия-лаборатория»
Реферат
Периодические движения бильярдного шара.
автор: ученица 9 класса «А»
Кузнецова Катя
Руководитель:
Москва
2013
Оглавление:
Введение 3
Глава №1 4
Глава №2 4
Заключение 6
Список литературы 6
Введение.
Тема «Периодические движения бильярдного шара» заинтересовала меня, так как методы исследования бильярдных систем (например, анализ поведения бильярдных траекторий), с одной стороны, примыкают к традиционной геометрии, а с другой — лежат на стыке отраслей современной математики и теоретической механики. Будучи, как правило, вполне элементарными, эти методы позволяют получить далеко не элементарные выводы.
Общая математическая проблема бильярда заключается в том, чтобы описать возможные типы бильярдных траекторий в данной области Q. Простейший принцип такого описания — разделение траекторий на периодические, или замкнутые, и остальные — непериодические.
Интерес представляют и такие вопросы: Какое число звеньев может иметь периодическая траектория? Какие периоды имеют периодические траектории в данной области?
Бильярд, родиной которого считается Китай, имеет многовековую историю. Первые известия о его появлении в Европе относятся к XVI веку, а в Россию бильярд был завезен из Голландии Петром I. Новинка быстро завоевала популярность. ( XVII-XVIII вв). В настоящее время эта игра увлекает многих людей разных профессий и возрастов. Современная теория бильярдов является одним из актуальных направлений математической физики. Ее основы были заложены советским математиком и его школой.
Проблемы существования периодических траекторий, исследования их динамических и геометрических свойств продолжают интенсивно обсуждаться в настоящее время. Подобно тому, как игра в кости вызвала в жизни «исчисление вероятностей», бильярдная игра послужила источником серьезных научных исследований по механики и математики.
Впервые о математическом базисе бильярдной игры заговорил Гаспар Густав Кориолис в своей книге «Математическая теория явлений бильярдной игры» в 1835 году. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа. Однако особого интереса у современников книга не вызвала: ни у математиков, ни у бильярдистов.
Одной из классических динамических систем является бильярд Биркгофа - задача об исследовании движения точки в плоской области, ограниченной гладкой замкнутой выпуклой кривой. Внутри области точка движется прямолинейно, а отскок криво! Происходит по закону "угол падения равен углу отражения". Биркгроф обнаружил такое важное свойство выпуклого бильярда, как наличие бесконечного количества периодических траекторий.
В своей работе я рассмотрю вопросы периодических движений бильярдного шара, теорему Биркгофа и различные поведения бильярдной траектории.
Глава 1.
Бильярдная игра – источник научных исследований по механике и математике. Но в математических исследованиях реальный бильярд заменяют его моделью «математический бильярд», представляющая собой стол без луз с упругими бортами, где шар – это точка, движущаяся без трения и отражающаяся от стенок по закону «угол падения равен углу отражения».
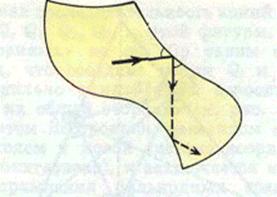
Шар движется вдоль ломаной, которая называется бильярдная траектория. Периодическая бильярдная траектории – это траектории, которые после некоторого числа отражений от границы повторяют сами себя. Например, в круглом бильярде периодическая траектория - это вписанный в круг правильный пятиугольник или правильная пятиконечная звезда.
Глава 2.
Изучение замкнутых, периодических бильярдных траекторий – классическая задача, впервые поставленная Джорджем Биркгофом. Он доказал нижнюю оценку на количество замкнутых бильярдных траекторий данной длины в любой плоской области.
В выпуклой ограниченной фигуре Q с гладкой границей можно обнаружить периодическую траекторию из двух звеньев. Для этого возьмем 2 наиболее удаленные точки А и В фигуры Q и соединим их отрезком. Получится замкнутая ломаная АВА – это дважды пройденный отрезок АВ, т. е. АВ и есть периодическая траектория.
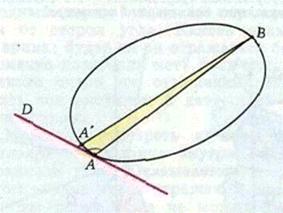
Для того, чтобы определить есть ли траектории с большим числом звеньев, надо построить треугольник АВС, с наибольшим периметром и вписанным в фигуру Q. Американский математик (1доказал, что n-угольник, имеющий наибольший периметр среди вписанных в Q n-угольников, является периодической бильярдной траекторией. Из этого мы можем сделать вывод, что АВС – это периодическая траектория.
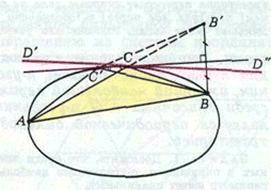
Но метод Биркгофа не «работает», если бильярдный стол имеет точки излома. ,т. к вершины вписанного многоугольника наибольшего периметра могут попасть в угловые точки границы. Но для остроугольного треугольника есть выход, и он заключается в замене максимального периметра на минимальный. Поиск бильярдных траекторий среди вписанных ломаных, максимальной и минимальной длины отражает общематематический принцип: во многих задачах полезно и важно рассматривать экстремальные значения подходящих величин.
Устойчивые траектории при малом изменении угла разрушаются, но в тупоугольном треугольнике такого недостатка нет. Т. е. периодические траектории в треугольных бильярдах весьма чувствительны к форме треугольника. Прохождение через угловую точку границы – причина разрушения или появления периодической траектории при деформации треугольника.
В произвольном прямоугольном треугольнике существуют периодические траектории со сколь угодно большим числом звеньев. Для остроугольных треугольников это не известно, хотя и доказано, что для любого заданного числа n найдется остроугольный треугольник, в котором имеются периодические траектории более чем n звеньев.
Заключение.
В своей работе я рассмотрела теорему Биркгофа, поведение бильярдного шара и наличие периодических траекторий в различных фигурах бильярдного стола, используя статью из журнала «Квант». Бильярдная игра, как и игра в кости, - это интересный источник научных исследований по механике и математике.
Список литературы:
Периодические движения бильярдного шара. Журнал «Квант». 1989



