В частности, если ![]() , то отображение A*: V→V называется сопряженным к оператору A, если (Ax, y) = (x, A*y)
, то отображение A*: V→V называется сопряженным к оператору A, если (Ax, y) = (x, A*y) 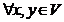 .
.
Теорема о линейности сопряженного оператора
Оператор, сопряженный к линейному оператору, также является линейным оператором.
Теорема о существовании и единственности сопряженного оператора
Для любого оператора ![]() существует, и притом единственный, сопряженный оператор.
существует, и притом единственный, сопряженный оператор.
Свойства сопряженного оператора
Операция сопряжения линейного оператора обладает следующими свойствами:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Данные свойства выполнены для любых операторов, для которых определены данные операции.
Биортогональные базисы
Две системы векторов ![]() и
и 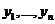 в унитарном (или евклидовом) пространстве называют биортогональной системой, если
в унитарном (или евклидовом) пространстве называют биортогональной системой, если ![]() , где
, где ![]() - символ Кронекера, т. е.
- символ Кронекера, т. е. 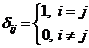 .
.
Биортогональная система двух базисов линейного пространства 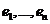 и
и ![]() называется биортогональной парой базисов.
называется биортогональной парой базисов.
Теорема о матрицах двух сопряженных операторов в паре биортогональных базисов
В паре биортогональных базисов ![]() и
и ![]() унитарного (евклидова) пространства
унитарного (евклидова) пространства ![]() матрицы операторов
матрицы операторов 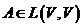 и
и ![]() связаны соотношением: (A*)f = (Ae)H.
связаны соотношением: (A*)f = (Ae)H.
То есть, матрица сопряженного оператора в базисе ![]() равна сопряженной матрице исходного оператора в базисе
равна сопряженной матрице исходного оператора в базисе ![]() .
.
(Напомним, что сопряженная к матрице A получается в результате ее транспонирования и комплексного сопряжения всех элементов: AH = ![]() ).
).
Самосопряженный оператор
Линейный оператор ![]() , действующий в унитарном (или евклидовом) пространстве, называется самосопряженным, если
, действующий в унитарном (или евклидовом) пространстве, называется самосопряженным, если ![]() , то есть,
, то есть, ![]()
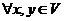 .
.
В евклидовом пространстве такой оператор называют самосопряженным (или симметрическим), а в унитарном пространстве – эрмитовым.
Свойства самосопряженного оператора
1) Самосопряженный оператор нормален.
2) Оператор самосопряжен тогда и только тогда, когда в любом ортонормированном базисе он имеет самосопряженную матрицу
3) Определитель самосопряженного оператора вещественен.
4) Если подпространство ![]() инвариантно относительно самосопряженного оператора
инвариантно относительно самосопряженного оператора ![]() , то подпространство
, то подпространство ![]() тоже инвариантно относительно этого оператора
тоже инвариантно относительно этого оператора
5) Самосопряженный оператор в любом инвариантном подпространстве индуцирует самосопряженный оператор.
Спектральная характеристика самосопряженного оператора
Нормальный оператор в унитарном (евклидовом) пространстве самосопряжен тогда и только тогда, когда все корни его характеристического многочлена вещественны (действительны).
Таким образом, у самосопряженного оператора все корни его характеристического многочлена являются вещественными (действительными).
Каноническая форма матрицы самосопряженного оператора
Оператор, действующий в унитарном (евклидовом) пространстве, самосопряжен тогда и только тогда, когда существует ортонормированный базис, в котором его матрица имеет вещественна (действительна) и диагональна. Любая такая матрица самосопряженного оператора называется его канонической матрицей.
Нормальный оператор
Пусть ![]() - унитарное или евклидово пространство. Линейный оператор
- унитарное или евклидово пространство. Линейный оператор ![]() называется нормальным оператором, если
называется нормальным оператором, если ![]()
Теорема о собственных векторах нормального и сопряженного к нему оператора
Собственный вектор нормального оператора, соответствующий собственному значению ![]() , является собственным вектором сопряженного оператора, соответствующим собственному значению
, является собственным вектором сопряженного оператора, соответствующим собственному значению ![]() .
.
Теорема о собственных векторах нормального оператора, соответствующих различным собственным значениям
Собственные векторы нормального оператора, соответствующие различным собственным значениям, попарно ортогональны.
Критерий нормальности оператора в унитарном пространстве
Оператор, действующий в унитарном пространстве, нормален тогда и только тогда, когда существует ортонормированный базис из его собственных векторов.
Лекция № 14. Раздел 7. Линейные операторы в евклидовом (унитарном) пространстве
Темы:
7.2. Ортогональный (унитарный) оператор
7.3. Эрмитов оператор
7.2. Ортогональный (унитарный) оператор
Ортогональный (унитарный) оператор
Линейный оператор ![]() , действующий в унитарном (или евклидовом) пространстве, называется унитарным (соответственно, ортогональным) оператором, если
, действующий в унитарном (или евклидовом) пространстве, называется унитарным (соответственно, ортогональным) оператором, если ![]() , где
, где ![]() - единичный оператор.
- единичный оператор.
Ортогональная (унитарная) матрица
Матрица U из Сnxn называется унитарной, если ![]() .
.
Матрица Q из Rnxn называется ортогональной, если ![]() .
.
Замечание: обозначение ![]() обозначает комплексное сопряжение, т. е. матрицу U транспонируют, и все элементы полученной матрицы заменяют на комплексно сопряженные.
обозначает комплексное сопряжение, т. е. матрицу U транспонируют, и все элементы полученной матрицы заменяют на комплексно сопряженные.
Три свойства унитарного и ортогонального операторов
Пусть дан унитарный (ортогональный) оператор 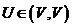 . Тогда
. Тогда
1) ![]()
2) Его матрица в любом ортонормированном базисе ортогональна.
3) Оператор U сохраняет скалярное произведение: ![]()
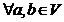 . В частности, он сохраняет длину. Иногда именно это свойство постулируют в качестве определения унитарного (ортогонального) оператора.
. В частности, он сохраняет длину. Иногда именно это свойство постулируют в качестве определения унитарного (ортогонального) оператора.
Критерий унитарности оператора
В унитарном (евклидовом) пространстве ![]() следующие утверждения равносильны:
следующие утверждения равносильны:
1) Оператор ![]() унитарен (ортогонален)
унитарен (ортогонален)
2) ![]()
3) ![]()
4) Оператор ![]() сохраняет скалярное произведение:
сохраняет скалярное произведение: ![]()
![]()
5) Оператор ![]() сохраняет длину:
сохраняет длину: 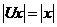
![]()
6) Оператор ![]() переводит любой ортонормированный базис в ортонормированный базис
переводит любой ортонормированный базис в ортонормированный базис
7) Оператор ![]() переводит хотя бы один ортонормированный базис в ортонормированный базис
переводит хотя бы один ортонормированный базис в ортонормированный базис
Спектральная характеристика унитарного оператора
Нормальный оператор в унитарном пространстве унитарен тогда и только тогда, когда все его собственные значения по модулю равны единице: ![]() .
.
Таким образом, у унитарного оператора все корни его собственные значения по модулю равны единице.
В частности, у ортогонального оператора в евклидовом пространстве все его собственные значения равны ![]() .
.
Каноническая форма матрицы унитарного оператора
В пространстве ![]() существует ортонормированный базис
существует ортонормированный базис ![]() , в котором матрица унитарного оператора
, в котором матрица унитарного оператора ![]() имеет диагональную форму:
имеет диагональную форму:
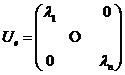 , где
, где ![]() .
.
Такая форма матрицы называется канонической формой матрицы унитарного оператора.
Каноническая форма матрицы ортогонального оператора
Для любого ортогонального оператора ![]() в евклидовом пространстве существует ортонормированный базис, в котором его матрица имеет квазидиагональную форму с клетками вида:
в евклидовом пространстве существует ортонормированный базис, в котором его матрица имеет квазидиагональную форму с клетками вида:
![]() ,
, ![]() на главной диагонали.
на главной диагонали.
7.3. Эрмитов оператор
Эрмитов оператор
Самосопряженный оператор в унитарном пространстве называется эрмитовым.
Эрмитова матрица
Эрмитовой матрицей U называют комплексную самосопряженную матрицу - такую, для которой 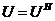 .
.
Лекция № 15. Раздел 8. Евклидовы и унитарные пространства.
Темы:
8.1. Скалярное произведение
8.2. Евклидово пространство
8.1. Скалярное произведение
Скалярное произведение
Пусть ![]() - вещественное (действительное) или комплексное пространство (с основным полем P = R или P = C).
- вещественное (действительное) или комплексное пространство (с основным полем P = R или P = C).
Отображение ![]() называют скалярным произведением, если оно удовлетворяет следующим аксиомам: для
называют скалярным произведением, если оно удовлетворяет следующим аксиомам: для 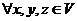 и
и ![]() :
:
1) ![]() (в случае, когда V - действительное пространство, выполняется равенство (x, y) = (y, x))
(в случае, когда V - действительное пространство, выполняется равенство (x, y) = (y, x))
2) ![]()
3) ![]()
4) ![]() , причем
, причем 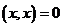 , когда
, когда ![]()
Длина вектора
Длиной вектора ![]() называется арифметическое (неотрицательное) значение квадратного корня из его скалярного квадрата:
называется арифметическое (неотрицательное) значение квадратного корня из его скалярного квадрата: 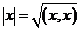
Теорема. Неравенства треугольника
В евклидовом (унитарном) пространстве для любых векторов из этого пространства имеют место неравенства:
![]()
Очевидные следствия:
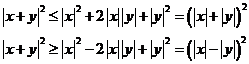
8.2. Евклидово пространство
Вещественное (действительное) евклидово пространство
Вещественное линейное пространство со скалярным произведением называют евклидовым пространством. Как правило, евклидовы пространства обозначаются буквой E.
Комплексное евклидово (унитарное) пространство
Комплексное линейное пространство со скалярным произведением называют унитарным пространством. Как правило, евклидовы пространства обозначаются буквой U.
Пять свойств скалярного произведения
Пусть E – евклидово пространство, U – унитарное пространство.
1) ![]()
![]()
2) ![]()
![]() в случае унитарного пространства U, и
в случае унитарного пространства U, и
![]() в случае евклидова пространства E.
в случае евклидова пространства E.
3) ![]() ,
, ![]()
4) ![]()
5) Любое подпространство евклидова (унитарного) пространства является евклидовым (унитарным) пространством.
Неравенство Коши-Буняковского
Для любых двух векторов ![]() имеет место неравенство
имеет место неравенство ![]() .
.
Другая форма записи это неравенства выглядит так: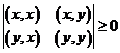
Теорема об изоморфизме евклидовых (унитарных) пространств.
Два евклидовых (унитарных) пространства изоморфны тогда и только тогда, когда равны их размерности.
Метрика
Метрикой на множестве M называется отображение, которое каждой упорядоченной паре элементов 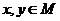 ставит в соответствие действительное число
ставит в соответствие действительное число 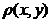 такое, что:
такое, что:
1) ![]() ,
, ![]()
2) ![]()
3) ![]() ,
, ![]()
4) ![]() ,
, ![]()
Метрическое пространство
Множество ![]() называют метрическим пространством, если на нем определена какая-либо метрика.
называют метрическим пространством, если на нем определена какая-либо метрика.
Заметим, что зачастую на одном и том же множестве возможно определить различные метрики и, соответственно, получить различные метрические пространства. Для явного указания метрики метрическое пространство часто обозначают парой (M, ![]() ).
).
Изометрия
Евклидовы пространства ![]() и
и ![]() называют изоморфными, если существует биективное отображение
называют изоморфными, если существует биективное отображение ![]() , которое сохраняет законы композиции и скалярное произведение, то есть:
, которое сохраняет законы композиции и скалярное произведение, то есть:
1) ![]()
2) 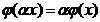
3) ![]()
Лекция № 16. Раздел 8. Евклидовы и унитарные пространства.
Темы:
8.3. Ортогональные, ортонормированные системы
8.4. Процесс ортогонализации Грама-Шмидта
8.5. Матрица Грама
8.3. Ортогональные, ортонормированные системы
Ортогональные векторы
Два вектора ![]() называются ортогональными, если
называются ортогональными, если ![]() .
.
Ортонормированная система
Система векторов ![]() называется ортонормированной системой, если
называется ортонормированной системой, если ![]()
Теорема о линейной независимости ортогональной системы
Ортогональная система всегда векторов является линейно независимой.
Теорема о вычислении координат вектора в ортонормированном базисе
В евклидовом (унитарном) пространстве координаты 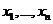 вектора
вектора ![]() в базисе
в базисе ![]() , состоящем из векторов
, состоящем из векторов 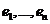 , вычисляются по правилу:
, вычисляются по правилу: 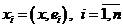 тогда и только тогда, когда
тогда и только тогда, когда ![]() - ортонормированный базис.
- ортонормированный базис.
Теорема о вычислении скалярного произведения векторов в ортонормированном базисе
В евклидовом (унитарном) пространстве скалярное произведение векторов 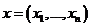 и
и ![]() , заданных своими координатами в базисе
, заданных своими координатами в базисе ![]() , вычисляется по правилу
, вычисляется по правилу ![]() тогда и только тогда, когда базис
тогда и только тогда, когда базис ![]() - ортонормированный.
- ортонормированный.
Теорема о существовании ортонормированного базиса
В любом конечномерном евклидовом (унитарном) пространстве существует ортонормированный базис.
8.4. Процесс ортогонализации Грама-Шмидта
Процесс ортогонализации Грама-Шмидта
Алгоритм построения ортонормированной системы e1, e2, … en по заданной системе![]() .
.
Шаг 1. Полагая ![]() , находим
, находим 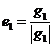 .
.
Шаг k (k>1). Полагаем 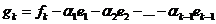 , где
, где ![]() ,
, 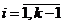 , и находим
, и находим ![]() .
.
(Например, g2 = f2 – (f2, e1)e1)
Таким образом, за n шагов мы получим ортонормированную систему e1, e2, … en.
8.5. Матрица Грама
Матрица Грама
Матрицей Грама системы векторов ![]() евклидова (унитарного) пространства называется квадратная матрица вида:
евклидова (унитарного) пространства называется квадратная матрица вида:
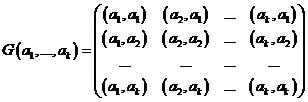
Критерий линейной (не)зависимости системы векторов в евклидовом (унитарном) пространстве
Система векторов ![]() евклидова (унитарного) пространства линейно зависима тогда и только тогда, когда
евклидова (унитарного) пространства линейно зависима тогда и только тогда, когда 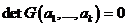 (т. е. когда определитель матрицы Грама этой системы равен нулю).
(т. е. когда определитель матрицы Грама этой системы равен нулю).
Теорема об определителе матрицы Грама линейно независимой системы векторов
Определитель матрицы Грама линейно независимой системы векторов в евклидовом (унитарном) пространстве положителен.
Лекция № 17. Раздел 9. Жорданова форма матрицы
Темы:
9.1. Жорданова клетка, жорданова матрица
Жорданова клетка
Матрица 
называется жордановой клеткой ![]() -го порядка.
-го порядка.
Эта матрица имеет:
1) характеристический многочлен 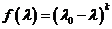
2) собственное значение ![]() кратности
кратности ![]()
3) собственные векторы, которые являются нетривиальными решениями однородной системы уравнений с матрицей 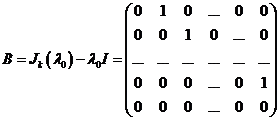 , ранг которой равен
, ранг которой равен ![]() .
.
Нильпотентный линейный оператор
Линейный оператор ![]() называется нильпотентным, если существует число q такое, что
называется нильпотентным, если существует число q такое, что 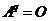 .
.
Индекс нильпотентности (высота) оператора
Наименьшее число q, для которого 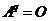 , называется индексом нильпонетности, или высотой оператора.
, называется индексом нильпонетности, или высотой оператора.
Прямая сумма линейных операторов
Если ![]() - прямая сумма подпространств
- прямая сумма подпространств ![]() линейного пространства
линейного пространства ![]() , инвариантных относительно линейного оператора
, инвариантных относительно линейного оператора 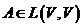 , то оператор
, то оператор ![]() называется прямой суммой индуцированных операторов
называется прямой суммой индуцированных операторов ![]() .
.
Иными словами, для любого вектора ![]() с разложением
с разложением 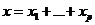 ,
, ![]() ,
, ![]() , имеет место равенство
, имеет место равенство 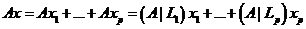 .
.
Корневой вектор линейного оператора
Пусть ![]() - собственное значение оператора
- собственное значение оператора ![]() . Вектор
. Вектор ![]() называется корневым вектором оператора
называется корневым вектором оператора ![]() , соответствующим собственному значению
, соответствующим собственному значению ![]() , если
, если ![]() при некотором
при некотором 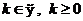 .
.
Высота корневого вектора
Высотой корневого вектора x, соответствующего собственному значению ![]() , называется такое наименьшее число
, называется такое наименьшее число ![]() , что
, что ![]() .
.
Присоединенный вектор
Корневые векторы высоты ![]() называются присоединенными векторами
называются присоединенными векторами ![]() -го порядка.
-го порядка.
Таким образом, корневой вектор – это либо нулевой вектор, либо собственный вектор, либо присоединенный вектор.
Корневое подпространство линейного оператора
Множество всех корневых векторов линейного оператора ![]() , соответствующих собственному значению
, соответствующих собственному значению ![]() , называется корневым подпространством линейного оператора
, называется корневым подпространством линейного оператора ![]() , соответствующим собственному значению
, соответствующим собственному значению ![]() .
.
Обозначение корневого подпространства: 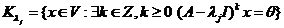
Лекция № 18 (обзорная). Разделы 1-9 (обзор). Примеры задач, решаемых с помощью освоенных методов.
Применение аппарата билинейных функций и линейных операторов для решения задачи приведения к каноническому виду уравнения кривых и поверхностей второго порядка. Указание нового (канонического) базиса. Схематическое изображение кривой (поверхности) в «новом» и в «старом» базисах.
Применение метода нахождения ортогональной проекции и ортогональной составляющей вектора для решения некорректно поставленных задач в частности, несовместных систем линейных алгебраических уравнений.
Применение жордановой формы матрицы для решения систем линейных дифференциальных уравнений в частных производных. Применение жордановой формы матрицы оператора для вычисления n-й степени оператора, нахождения функций от оператора – вида eA.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |





