Критерий скалярного произведения
Пусть ![]() - вещественное линейное пространство. Отображение
- вещественное линейное пространство. Отображение ![]() представляет собой скалярное произведение в пространстве
представляет собой скалярное произведение в пространстве ![]() тогда и только тогда, когда оно является симметричной билинейной формой, полярной к положительно определенной квадратичной форме.
тогда и только тогда, когда оно является симметричной билинейной формой, полярной к положительно определенной квадратичной форме.
Билинейные и квадратичные формы
в евклидовом (унитарном) линейном пространстве
Теорема о соответствии между квадратичными формами и симметрическими линейными преобразованиями
Для любой квадратичной формы f(x) = ![]() в евклидовом пространстве
в евклидовом пространстве ![]() существует, и притом единственный, симметрический оператор (точнее, линейное преобразование)
существует, и притом единственный, симметрический оператор (точнее, линейное преобразование) 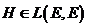 , такой что
, такой что ![]()
![]() , где
, где![]() - скалярное произведение векторов
- скалярное произведение векторов ![]() и
и ![]() .
.
Лекция № 9. Раздел 5. Линейные операторы - общие сведения.
Темы:
5.1. Линейный оператор, линейное преобразование, линейный функционал
5.2. Отдельные виды линейных операторов
5.3. Матрица линейного оператора, линейной формы
5.1. Линейный оператор, линейное преобразование, линейный функционал
Линейный оператор
Пусть ![]() и
и ![]() - линейные пространства над общим полем
- линейные пространства над общим полем ![]() .
.
Отображение ![]() называется линейным оператором, действующим из пространства
называется линейным оператором, действующим из пространства ![]() в пространство
в пространство ![]() , если для любых
, если для любых ![]()
![]() верны равенства:
верны равенства:
1) 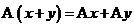
2) 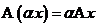
Множество всех линейных операторов из ![]() в
в ![]() обозначается через
обозначается через 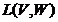 .
.
Линейное преобразование
Линейный оператор, действующий из линейного пространства в то же линейное пространство, называется линейным преобразованием.
В нашем курсе мы будем вместо термина "линейное преобразование" часто использовать термин "линейный оператор".
Линейный функционал
Линейный оператор, отображающий векторы линейного пространства в основное поле, называется линейным функционалом, или линейной формой.
Простейшие свойства линейных операторов
1) Линейный оператор переводит нулевой вектор в нулевой вектор
2) Линейный оператор сохраняет линейные комбинации.
3) Линейный оператор сохраняет линейную зависимость
5.2. Отдельные виды линейных операторов
Оператор проектирования
Пусть линейное пространство V является прямой суммой двух своих подпространств V1 и V2: ![]() . При этом любой вектор x линейного пространства V можно (единственным образом) представить в виде суммы двух векторов из этих подпространств:
. При этом любой вектор x линейного пространства V можно (единственным образом) представить в виде суммы двух векторов из этих подпространств: ![]() , где
, где ![]() , а
, а ![]() .
.
Отображение ![]() , определенное правилом
, определенное правилом 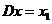 , называется оператором проектирования пространства
, называется оператором проектирования пространства ![]() на подпространство
на подпространство ![]() параллельно
параллельно ![]() . Отображение D является линейным.
. Отображение D является линейным.
Оператор отражения
Пусть линейное пространство V является прямой суммой двух своих подпространств V1 и V2: ![]() . При этом любой вектор x линейного пространства V можно (единственным образом) представить в виде суммы двух векторов из этих подпространств:
. При этом любой вектор x линейного пространства V можно (единственным образом) представить в виде суммы двух векторов из этих подпространств: 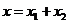 , где
, где ![]() , а
, а ![]() .
.
Отображение ![]() , определенное правилом
, определенное правилом 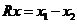 , называется оператором отражения пространства
, называется оператором отражения пространства ![]() относительно
относительно ![]() . Отображение R является линейным.
. Отображение R является линейным.
Нулевой оператор
Отображение ![]() , которое каждый вектор
, которое каждый вектор ![]() переводит в нулевой вектор
переводит в нулевой вектор ![]() , называется нулевым оператором. Нулевой оператор является линейным.
, называется нулевым оператором. Нулевой оператор является линейным.
Единичный оператор
Отображение ![]() , которое каждый вектор
, которое каждый вектор ![]() переводит в него же, называется единичным оператором.
переводит в него же, называется единичным оператором.
5.3. Матрица линейного оператора, линейной формы
Матрица линейного оператора
Пусть ![]() и
и 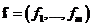 - базисы линейных пространств
- базисы линейных пространств ![]() и
и ![]() соответственно. Линейный оператор
соответственно. Линейный оператор ![]() однозначно определяется заданием векторов
однозначно определяется заданием векторов ![]() . В свою очередь, эти векторы однозначно определены своими координатами в базисе
. В свою очередь, эти векторы однозначно определены своими координатами в базисе ![]() , т. е. коэффициентами разложений:
, т. е. коэффициентами разложений:
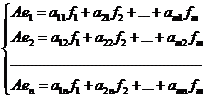
Матрица 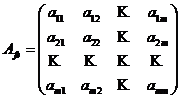 называется матрицей оператора
называется матрицей оператора ![]() в паре базисов
в паре базисов ![]() и
и ![]() .
.
Теорема о соответствии между матрицами и линейными операторами
Пусть ![]() ,
, 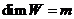 , тогда существует взаимно однозначное соответствие между линейными операторами
, тогда существует взаимно однозначное соответствие между линейными операторами ![]() и матрицами из
и матрицами из ![]() .
.
Теорема об изменении матрицы линейного оператора при переходе от одной пары базисов к другой
Матрицы ![]() и
и ![]() линейного оператора
линейного оператора 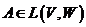 в различных парах базисов (e, f) и (t, s) связаны соотношением
в различных парах базисов (e, f) и (t, s) связаны соотношением ![]() , где
, где ![]() и
и ![]() - соответствующие матрицы перехода.
- соответствующие матрицы перехода.
Координаты образа вектора
Пусть даны два линейных пространства V и W с базисами e = (e1, …, en) и f = (f1, …, fm) соответственно. Пусть A – линейный оператор из V в W c матрицей Afe в паре базисов (e, f). Пусть A отображает вектор x (с координатами Xe = (x1, … xn) в базисе e) в вектор Ax = y (с координатами Yf = (y1, …, ym) в базисе f). Тогда
Yf = AfeXe.
Учитывая, что ![]() ,
, 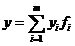 ,
, ![]() , можно выразить координаты вектора y через координаты вектора x и элементы матрицы A следующим образом :
, можно выразить координаты вектора y через координаты вектора x и элементы матрицы A следующим образом :
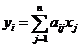 ,
, ![]()
Лекция № 10. Раздел 5. Линейные операторы - общие сведения.
Темы:
5.4. Образ, прообраз, ядро оператора
5.5. Пространство линейных операторов
5.4. Образ, прообраз, ядро оператора
Образ вектора
Результатом действия оператора ![]() на вектор
на вектор ![]() является вектор
является вектор ![]() , который называется образом вектора x.
, который называется образом вектора x.
Полный прообраз вектора
Пусть дан оператор ![]() и пусть
и пусть ![]() , где
, где ![]() ,
, ![]() .
.
Тогда вектор ![]() называется прообразом вектора
называется прообразом вектора ![]() .
.
Полным прообразом вектора ![]() называется множество всех векторов
называется множество всех векторов ![]() , для которых
, для которых ![]() .
.
Образ оператора
Образом линейного оператора ![]() (обозначается ImA) называется множество всех его значений в W. То есть,
(обозначается ImA) называется множество всех его значений в W. То есть, ![]() .
.
Ядро оператора
Ядром линейного оператора ![]() (обозначается kerA) называется множество всех векторов, образом которых является ноль-вектор
(обозначается kerA) называется множество всех векторов, образом которых является ноль-вектор![]() . То есть,
. То есть,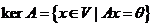 .
.
Ранг линейного оператора
Рангом линейного оператора A (обозначается rgA) называется размерность его образа: ![]()
Дефект линейного оператора
Дефектом (обозначается defA) линейного оператора A называется размерность его ядра: ![]()
Теорема о ранге линейного оператора
Ранг линейного оператора равен рангу его матрицы в произвольной паре базисов.
То есть, для любой пары базисов (e, f) выполняется равенство:
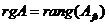
Теорема о ранге и дефекте
Если ![]() , то
, то 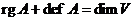 .
.
То есть, сумма ранга и дефекта оператора всегда равна размерности пространства прообразов.
5.5. Пространство линейных операторов
Сумма линейных операторов
Суммой A+B линейных операторов ![]() называется отображение
называется отображение 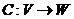 , определяемое следующим образом:
, определяемое следующим образом: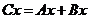 ,
, ![]()
Таким образом, по определению, ![]()
(A+B)x = Ax + Bx.
Произведение линейного оператора на число
Произведением линейного оператора ![]() на число
на число ![]() (обозначается
(обозначается ![]() ) называется отображение
) называется отображение ![]() , определяемое следующим образом:
, определяемое следующим образом: 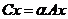 .
.
Таким образом, по определению, для любого вектора x и любого числа ![]()
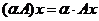
Пространство линейных операторов
Множество ![]() линейных операторов, действующих из
линейных операторов, действующих из ![]() в
в ![]() , является линейным пространством относительно операций сложения и умножения на число.
, является линейным пространством относительно операций сложения и умножения на число.
Теорема о пространстве линейных операторов
Множество ![]() - линейное пространство над полем
- линейное пространство над полем ![]() относительно введенных выше операций сложения и умножения на число.
относительно введенных выше операций сложения и умножения на число.
Изоморфизм линейных операторов
Если ![]() ,
, 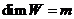 , то линейное пространство операторов
, то линейное пространство операторов 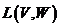 изоморфно пространству матриц
изоморфно пространству матриц ![]()
Произведение линейных операторов
Пусть ![]() - линейные пространства над полем
- линейные пространства над полем ![]() . Произведением линейных операторов
. Произведением линейных операторов 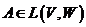 и
и ![]() (обозначается
(обозначается ![]() ) называется отображение
) называется отображение 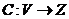 , определяемое следующим образом:
, определяемое следующим образом: 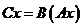 .
.
Таким образом, по определению,
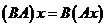 .
.
Сопряженное пространство
Множество ![]() всех линейных форм в линейном пространстве
всех линейных форм в линейном пространстве ![]() образует линейное пространство относительно операций сложения и умножения на число:
образует линейное пространство относительно операций сложения и умножения на число:
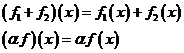
Линейное пространство всех линейных форм на пространстве ![]() называют сопряженным пространством к пространству
называют сопряженным пространством к пространству ![]() и обозначают
и обозначают ![]() .
.
Алгебра линейных операторов
Линейное пространство над полем ![]() , которое является кольцом и удовлетворяет условиям
, которое является кольцом и удовлетворяет условиям ![]() , называется алгеброй (или линейного алгеброй) над полем
, называется алгеброй (или линейного алгеброй) над полем ![]() .
.
Согласно этому, линейное пространство операторов, действующих в линейных пространствах над полем P, является алгеброй над этим полем.
Многочлен от оператора
Как и в любом кольце, оператор ![]() можно возводить в степень
можно возводить в степень ![]() , и если
, и если 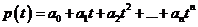 - некий произвольный многочлен над полем
- некий произвольный многочлен над полем ![]() от переменной
от переменной ![]() , то однозначно определен оператор
, то однозначно определен оператор ![]() , называемый многочленом от оператора
, называемый многочленом от оператора ![]() .
.
Определитель линейного оператора
Определителем линейного оператора ![]() называется определитель матрицы этого оператора в произвольном базисе.
называется определитель матрицы этого оператора в произвольном базисе.
Обратный оператор
Пусть дан оператор ![]() (то есть, линейное преобразование). Отображение
(то есть, линейное преобразование). Отображение ![]() называется обратным оператором к оператору
называется обратным оператором к оператору ![]() , если
, если 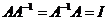
Теорема о виде матрицы произвольного линейного оператора в паре канонических базисов
Пусть ![]() ,
, 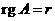 ,
, ![]() ,
, 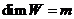 . Тогда существуют базисы
. Тогда существуют базисы ![]() и
и ![]() пространств
пространств ![]() и
и ![]() , в которых оператор имеет матрицу
, в которых оператор имеет матрицу ![]() вида:
вида:
 , в которой все элементы равны нулю, кроме первых
, в которой все элементы равны нулю, кроме первых ![]() диагональных элементов, равных 1.
диагональных элементов, равных 1.
Теорема о матрице обратного оператора
Матрица оператора ![]() в произвольном базисе является обратной к матрице оператора
в произвольном базисе является обратной к матрице оператора ![]() в том же базисе.
в том же базисе.
Лекция № 11. Раздел 6. Линейные преобразования
Темы:
6.1. Собственное значение, собственный вектор
Линейные операторы, действующие в одном (произвольном) линейном пространстве
Линейный оператор, действующий в одном линейном пространстве
Линейное отображение ![]() называется линейным преобразованием пространства
называется линейным преобразованием пространства ![]() в себя, или линейным оператором, действующем в пространстве
в себя, или линейным оператором, действующем в пространстве ![]() .
.
Матрица линейного оператора, действующего в одном линейном пространстве
Матрица оператора ![]() представляет собой квадратную матрицу..
представляет собой квадратную матрицу..
Инвариантное подпространство
Пусть ![]() - линейное пространство над полем
- линейное пространство над полем ![]() , и дан линейный оператор
, и дан линейный оператор 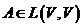 .
.
Линейное подпространство ![]() пространства
пространства ![]() называется инвариантным подпространством относительно оператора
называется инвариантным подпространством относительно оператора ![]() , если
, если ![]()
![]() , т. е. при действии этого оператора любой вектор из этого подпространства переходит в вектор, находящийся в том же подпространстве.
, т. е. при действии этого оператора любой вектор из этого подпространства переходит в вектор, находящийся в том же подпространстве.
Индуцированный оператор
Пусть ![]() - подпространство пространства
- подпространство пространства ![]() , инвариантное относительно
, инвариантное относительно 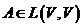 . Отображение
. Отображение 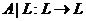 , определенное равенством
, определенное равенством 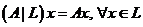 , называют индуцированным оператором, порожденным оператором
, называют индуцированным оператором, порожденным оператором ![]() . Это отображение является линейным отображением из L в L.
. Это отображение является линейным отображением из L в L.
Теорема о виде матрицы линейного оператора в пространстве – прямой сумме инвариантных подпространств
Если пространство ![]() является прямой суммой подпространств
является прямой суммой подпространств ![]() , инвариантных относительно оператора
, инвариантных относительно оператора 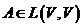 , то в пространстве
, то в пространстве ![]() существует базис, в котором матрица оператора
существует базис, в котором матрица оператора ![]() имеет квазидиагональную форму.
имеет квазидиагональную форму.
Собственное значение линейного оператора
Пусть дан оператор ![]() . Если для какого-либо ненулевого вектора x выполняется равенство
. Если для какого-либо ненулевого вектора x выполняется равенство ![]() , то число
, то число ![]() называется собственным значением оператора.
называется собственным значением оператора.
Спектр линейного оператора
Спектром линейного оператора называется множество всех его собственных значений.
Собственный вектор линейного оператора
Пусть дан оператор ![]() . Ненулевой вектор
. Ненулевой вектор ![]() называется собственным вектором оператора
называется собственным вектором оператора ![]() , если существует такое число
, если существует такое число ![]() , для которого
, для которого ![]() .
.
Теорема о собственных векторах с различными собственными значениями
Собственные векторы ![]() , соответствующие различным собственным значениям
, соответствующие различным собственным значениям ![]() , линейно независимы.
, линейно независимы.
Теорема о матрице линейного преобразования в базисе из собственных векторов
Матрица линейного оператора в базисе из собственных векторов представляет собой диагональную матрицу, на главной диагонали которой стоят соответствующие собственные значения.
Таким образом, такая матрица будет матрицей простой структуры.
Теорема о собственных значениях и собственных векторах в комплексном линейном пространстве
Произвольный линейный оператор ![]() , действующий в
, действующий в ![]() -мерном комплексном пространстве
-мерном комплексном пространстве ![]() , имеет:
, имеет:
1) ![]() собственных значений, если их считать столько раз, какова их кратность, как корня характеристического многочлена
собственных значений, если их считать столько раз, какова их кратность, как корня характеристического многочлена
2) хотя бы один собственный вектор
3) на любом инвариантном подпространстве - хотя бы один собственный вектор
Критерий наличия у оператора простой структуры
Линейный оператор ![]() имеет простую структуру тогда и только тогда, когда пространство является прямой суммой всех его собственных подпространств:
имеет простую структуру тогда и только тогда, когда пространство является прямой суммой всех его собственных подпространств: ![]()
Лекция № 12. Раздел 6. Линейные преобразования
Темы:
6.2. Характеристический многочлен линейного преобразования
Характеристический многочлен матрицы
Характеристическим многочленом квадратной матрицы ![]() называется функция вида
называется функция вида 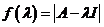 , где
, где ![]() - единичная матрица соответствующего размера
- единичная матрица соответствующего размера
В этом определении говорится о произвольной квадратной матрице, которая не обязана быть матрицей какого-то линейного оператора (хотя между такими матрицами и линейными операторами при фиксировании базиса можно установить взаимно однозначное соответствие).
Подобные матрицы
Матрицы ![]() называются подобными, если существует невырожденная матрица
называются подобными, если существует невырожденная матрица ![]() , такая что
, такая что 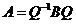
Характеристический многочлен линейного оператора
Характеристическим многочленом линейного оператора 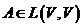 называется характеристический многочлен его матрицы в произвольном базисе:
называется характеристический многочлен его матрицы в произвольном базисе: ![]() , где
, где ![]() - матрица оператора,
- матрица оператора, ![]() - единичная матрица.
- единичная матрица.
Теорема о характеристических многочленах подобных матриц
Характеристические многочлены подобных матриц совпадают.
Теорема о корнях характеристического многочлена и собственных значениях линейного оператора
Пусть ![]() - линейное пространство над полем
- линейное пространство над полем ![]() . Число
. Число ![]() является собственным значением оператора
является собственным значением оператора ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() - корень его характеристического многочлена.
- корень его характеристического многочлена.
Собственное подпространство линейного оператора
Пусть λ - некое собственное значение линейного оператора ![]() . Собственным подпространством линейного оператора
. Собственным подпространством линейного оператора ![]() , соответствующим собственному значению λ, называется множество Wλ векторов (включая и нулевой вектор), для которых Ax = λx.
, соответствующим собственному значению λ, называется множество Wλ векторов (включая и нулевой вектор), для которых Ax = λx.
Алгебраическая кратность собственного значения линейного оператора
Алгебраической кратностью собственного значения λ линейного оператора называется кратность числа λ, как корня характеристического многочлена.
Геометрическая кратность собственного значения линейного оператора
Геометрической кратностью собственного значения ![]() называется размерность собственного подпространства
называется размерность собственного подпространства ![]() , соответствующего этому собственному значению.
, соответствующего этому собственному значению.
Оператор простой структуры
Линейный оператор ![]() называется оператором простой структуры, если в пространстве
называется оператором простой структуры, если в пространстве ![]() существует базис, состоящий только из его собственных векторов.
существует базис, состоящий только из его собственных векторов.
Матрица простой структуры
Квадратная матрица называется матрицей простой структуры, если она имеет n линейно независимых собственных векторов.
Теорема Гамильтона-Кэли
Линейный оператор, действующий в комплексном или вещественном пространстве, является корнем своего характеристического многочлена.
Лекция № 13. Раздел 7. Линейные операторы в евклидовом (унитарном) пространстве
Темы:
7.1. Сопряженный оператор, самосопряженный оператор
Линейные операторы,
действующие в (одном) евклидовом или унитарном пространстве
7.1. Сопряженный оператор, самосопряженный оператор
Сопряженный оператор
Пусть V и W – евклидовы пространства. Пусть дан оператор ![]() . Отображение
. Отображение 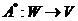 называют сопряженным оператором к оператору
называют сопряженным оператором к оператору ![]() , если
, если ![]() ,
, 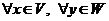 .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |





