Коротко: сумма подпространств называется прямой, если разложение любого вектора суммы по подпространствам единственно.
Прямая сумма подпространств – не есть какая-то новая операция над подпространствами. Это просто некоторое свойство ранее введенной суммы подпространств.
Если сумма подпространств прямая, то пересечение этих подпространств состоит из одного – нулевого - вектора.
Критерий прямой суммы подпространств
Для подпространств ![]() конечномерного линейного пространства
конечномерного линейного пространства ![]() следующие утверждения равносильны:
следующие утверждения равносильны:
1) Сумма подпространств ![]() - прямая
- прямая
2) Совокупность базисов подпространств ![]() линейно независима
линейно независима
3) Совокупность базисов подпространств ![]() образует базис суммы подпространств
образует базис суммы подпространств ![]()
4) Размерность суммы равна сумме размерностей: ![]()
5) Существует вектор из суммы ![]()
![]() , для которого разложение по подпространствам
, для которого разложение по подпространствам ![]() единственно.
единственно.
6) Произвольная система ненулевых векторов ![]() , взятых по одному из каждого линейного подпространства
, взятых по одному из каждого линейного подпространства ![]() , линейно независима
, линейно независима
7) Пересечение линейных подпространств ![]() - только ноль-вектор:
- только ноль-вектор: 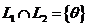
Дополнительное подпространство
Пусть L – линейное подпространство пространства V. Пространство ![]() называется дополнительным подпространством к L, если
называется дополнительным подпространством к L, если ![]() . Очевидно, что L – дополнительное подпространство к
. Очевидно, что L – дополнительное подпространство к ![]() .
.
Образно выражаясь, дополнительное подпространство как бы «дополняет» подпространство до полного пространства.
Теорема о существовании дополнительного подпространства
Для любого подпространства ![]() линейного пространства
линейного пространства ![]() существует дополнительное подпространство.
существует дополнительное подпространство.
Линейное многообразие
Пусть V – линейное пространство, L – некоторое его подпространство, ![]() - некоторый вектор пространства V. Множество H, состоящее из всех векторов вида
- некоторый вектор пространства V. Множество H, состоящее из всех векторов вида ![]() , где
, где ![]() , называется линейным многообразием пространства V (полученным сдвигом подпространства L на вектор
, называется линейным многообразием пространства V (полученным сдвигом подпространства L на вектор ![]() ).
).
Направляющее подпространство
Подпространство L в определении линейного многообразия называется направляющим подпространством линейного многообразия H.
Фактор-пространство
Пусть V – линейное пространство над полем P, L – его подпространство. Фактор-пространством линейного пространства V по подпространству L (обозначается V/L) называется множество, состоящее из классов эквивалентности H. Эти классы соответствуют всем линейным многообразиям, полученным из подпространства L: ![]() .
.
Правило ![]() определяет внешний закон композиции на V/L (умножение элемента H из V/L на число (или элемент основного поля P) α, правило
определяет внешний закон композиции на V/L (умножение элемента H из V/L на число (или элемент основного поля P) α, правило ![]() - внутренний закон композиции (сложение двух элементов – H1 и H2 - из V/L) .
- внутренний закон композиции (сложение двух элементов – H1 и H2 - из V/L) .
2.4. Подпространство решений однородной СЛАУ
Подпространства, задаваемые однородной системой линейных алгебраических уравнений
Это совокупность решений однородной системы линейных уравнений ![]() , где A – матрица коэффициентов линейных уравнений системы.
, где A – матрица коэффициентов линейных уравнений системы.
Лекция № 5. Раздел 3. Подпространства евклидова (унитарного) линейного пространства
Темы:
3.1. Ортогональное дополнение к подпространству
3.2. Ортогональная проекция, ортогональная составляющая
3.3. Расстояние от вектора до подпространства
3.1. Ортогональное дополнение к подпространству
Вектор, ортогональный к подпространству
Пусть L – линейное подпространство евклидова (унитарного) пространства ![]() . Вектор x называется ортогональным к подпространству L, если он ортогонален каждому вектору из этого подпространства. Обозначение:
. Вектор x называется ортогональным к подпространству L, если он ортогонален каждому вектору из этого подпространства. Обозначение: ![]() .
.
Ортогональное дополнение к подпространству
Пусть L – линейное подпространство евклидова пространства ![]() . Совокупность всех векторов
. Совокупность всех векторов 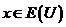 , ортогональных подпространству L, называется ортогональным дополнением к L. Обозначение:
, ортогональных подпространству L, называется ортогональным дополнением к L. Обозначение: ![]() .
.
Теорема об ортогональном дополнении как подпространстве
Ортогональное дополнение к подпространству является линейным подпространством того же пространства.
3.2. Ортогональная проекция, ортогональная составляющая
Ортогональная проекция вектора на подпространство
Пусть L – линейное подпространство евклидова (унитарного) пространства ![]() . Представим произвольный вектор
. Представим произвольный вектор 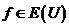 в виде суммы:
в виде суммы: ![]() , где
, где ![]() ,
, ![]() . Вектор g называется ортогональной проекцией вектора f на подпространство L, вектор h называется ортогональной составляющей.
. Вектор g называется ортогональной проекцией вектора f на подпространство L, вектор h называется ортогональной составляющей.
Ортогональная составляющая вектора
Ортогональной составляющей вектора f относительно подпространства L евклидова (унитарного) пространства ![]() называется слагаемое h в представлении вектора f в виде суммы:
называется слагаемое h в представлении вектора f в виде суммы: 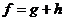 , где
, где ![]() ,
, ![]() .
.
Перпендикуляр, опущенный на подпространство
Перпендикуляром, опущенным из вектора f на подпространство L евклидова (унитарного) ![]() называется вектор h в разложении
называется вектор h в разложении ![]() , где
, где ![]() ,
, ![]() .
.
Наклонная к подпространству
Вектор f в разложении 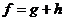 (где
(где ![]() ,
, ![]() ) называется наклонной к подпространству L евклидова (унитарного) пространства
) называется наклонной к подпространству L евклидова (унитарного) пространства ![]() .
.
Теорема о сумме подпространства и его ортогонального дополнения
Если ![]() - линейное подпространство пространства
- линейное подпространство пространства ![]() , то прямая сумма этого линейного подпространства и его ортогонального дополнения образует всё пространство
, то прямая сумма этого линейного подпространства и его ортогонального дополнения образует всё пространство ![]() :
: 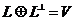
Следствие о существовании и единственности ортогональной проекции вектора на подпространство
Если ![]() - линейное подпространство пространства
- линейное подпространство пространства ![]() , то для любого вектора
, то для любого вектора ![]() существует, и притом единственное, представление f в виде суммы:
существует, и притом единственное, представление f в виде суммы: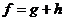 , где
, где ![]() .
.
3.3. Расстояние от вектора до подпространства
Расстояние от вектора до подпространства
Расстоянием от вектора до подпространства называется длина перпендикуляра, опущенного из этого вектора на подпространство (то есть, длина ортогональной составляющей вектора относительно данного подпространства).
Лекция № 6. Раздел 4. Билинейные и квадратичные формы.
Темы:
4.1. Линейная форма
4.2. Билинейная форма
Билинейные и квадратичные формы в произвольном линейном пространстве
4.1. Линейная форма
Линейная функция (линейная форма)
Пусть ![]() - линейное пространство над полем
- линейное пространство над полем ![]() . Функция f, отображающая вектор из пространства
. Функция f, отображающая вектор из пространства ![]() в число (элемент поля
в число (элемент поля ![]() )
) ![]() , называется линейной, если:
, называется линейной, если:
1) ![]() для всех векторов
для всех векторов 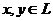 ,
,
2) ![]() для любого числа a (элемента поля
для любого числа a (элемента поля ![]() ) и любого вектора
) и любого вектора ![]()
Запись любой линейной формы в некотором (произвольном) базисе e выглядит так:
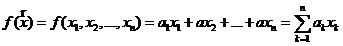 ,
,
где ![]() - вектор из пространства
- вектор из пространства ![]() с координатами x1, x2, …, xn в базисе e;
с координатами x1, x2, …, xn в базисе e; ![]() , - числа (элементы поля P), зависящие от базиса e и, конечно, от формы f.
, - числа (элементы поля P), зависящие от базиса e и, конечно, от формы f.
Заметим, что при выборе другого базиса e' соответствующий набор чисел будет, вообще говоря, другим: a1', a2', …, an'.
Матрица линейной формы
Матрицей A линейной формы f в базисе ![]() называется матрица-строка, состоящая из чисел - результатов действия линейной формы на векторы этого базиса:
называется матрица-строка, состоящая из чисел - результатов действия линейной формы на векторы этого базиса:
A = (a1, a2, …, an) = ![]() .
.
Пусть X =  - координаты вектора x в базисе e, A – матрица линейной формы f в том же базисе. Тогда значение f(x) равно произведению матрицы A на столбец X:
- координаты вектора x в базисе e, A – матрица линейной формы f в том же базисе. Тогда значение f(x) равно произведению матрицы A на столбец X:
f(x) = A·X.
Теорема об изменении матрицы линейной формы при переходе от одного базиса к другому
При переходе от базиса ![]() к базису
к базису ![]() (матрица перехода -
(матрица перехода - ![]() ) матрица линейной формы изменяется следующим образом:
) матрица линейной формы изменяется следующим образом:
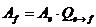
4.2. Билинейная форма
Билинейная функция (билинейная форма)
Пусть ![]() - линейное пространство над полем
- линейное пространство над полем ![]() . (числовая) Функция a двух векторных аргументов
. (числовая) Функция a двух векторных аргументов 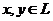 , отображающая упорядоченную пару векторов x, y в число (элемент поля P)
, отображающая упорядоченную пару векторов x, y в число (элемент поля P) 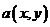 называется билинейной формой, если она линейна по каждому аргументу:
называется билинейной формой, если она линейна по каждому аргументу:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
![]() - любые векторы пространства L,
- любые векторы пространства L, ![]() - произвольное число (элемент поля P).
- произвольное число (элемент поля P).
Запись любой билинейной формы 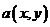 в некотором (произвольном) базисе e выглядит так:
в некотором (произвольном) базисе e выглядит так:
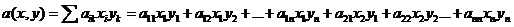 ,
,
где (x1, x2, …, xn) и (y1, y2, …, yn) – координаты в базисе e векторов x и y соответственно, a11, a12, …, a1n, …, ann – набор из n2 чисел (элементов поля P).
Заметим, что числа a11, a12, …, a1n, …, ann зависят от базиса e и, конечно, от самой формы a. При выборе другого базиса e' соответствующий набор чисел будет, вообще говоря, другим: a11', a12', …, ann'.
Матрица билинейной формы
Пусть дана билинейная форма ![]() и некоторый (произвольный) базис e.
и некоторый (произвольный) базис e.
Запишем действие билинейной формы в этом базисе:
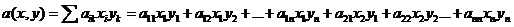
Матрицей A билинейной формы 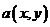 в базисе e называется следующая матрица:
в базисе e называется следующая матрица:
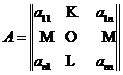
Каждый элемент aij матрицы A представляет собой результат действия билинейной формы ![]() на (упорядоченную) пару векторов базиса (ei, ej). Таким образом:
на (упорядоченную) пару векторов базиса (ei, ej). Таким образом:
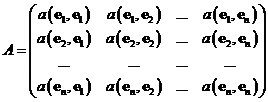
Теорема о матрице билинейной формы в фиксированном базисе
Произвольная квадратная матрица 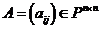 является матрицей единственной билинейной формы в заданном (фиксированном) базисе пространства.
является матрицей единственной билинейной формы в заданном (фиксированном) базисе пространства.
Теорема об изменении матрицы билинейной формы при переходе от одного базиса к другому
При переходе от базиса к базису (матрица перехода ![]() ) матрица билинейной формы изменяется следующим образом:
) матрица билинейной формы изменяется следующим образом:
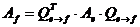
Ранг билинейной формы
Рангом билинейной формы называется ранг ее матрицы в произвольном базисе.
(не) Вырожденная билинейная форма
Билинейная форма ![]() называется вырожденной, если
называется вырожденной, если ![]() , и невырожденной, если
, и невырожденной, если 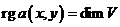
Симметричная билинейная форма
Билинейная форма ![]() называется симметричной, если для
называется симметричной, если для ![]()
![]() . Билинейная форма
. Билинейная форма ![]() называется кососимметричной (или кососимметрической), если для
называется кососимметричной (или кососимметрической), если для ![]()
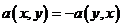 .
.
Теорема о матрице симметричной билинейной формы
Билинейная форма симметрична, если ее матрица симметрична хотя бы в одном (произвольном) базисе.
Матрица симметричной билинейной формы (в любом базисе) симметрична:
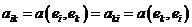 .
.
Замечание:
Матрица кососимметрической билинейной формы (в любом базисе) является кососимметрической: ![]() , для всех i, j. В частности, для всех i выполняется равенство
, для всех i, j. В частности, для всех i выполняется равенство![]() .
.
Лекция № 7. Раздел 4. Билинейные и квадратичные формы.
Темы:
4.3. Квадратичная форма
4.4. Канонический вид квадратичной формы
Билинейные и квадратичные формы в произвольном линейном пространстве
4.3. Квадратичная форма
Квадратичная форма
Пусть дана симметричная билинейная форма 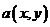 , т. е.
, т. е.![]() . Рассмотрим действие этой билинейной формы только на парах совпадающих векторов, т. е. a(x, x). Получим функцию, ставящую в соответствие каждому вектору x линейного пространства число (элемент основного поля P) f(x) = a(x, x). Функция f(x) =
. Рассмотрим действие этой билинейной формы только на парах совпадающих векторов, т. е. a(x, x). Получим функцию, ставящую в соответствие каждому вектору x линейного пространства число (элемент основного поля P) f(x) = a(x, x). Функция f(x) = ![]() называется квадратичной формой, соответствующей данной симметричной билинейной форме
называется квадратичной формой, соответствующей данной симметричной билинейной форме 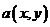 .
.
Полярная билинейная форма
Полярной для квадратичной формы f(x) = ![]() называется соответствующая симметричная билинейная форма
называется соответствующая симметричная билинейная форма ![]() .
.
Теорема о полярной билинейной форме
Полярная билинейная форма для любой квадратичной формы определена однозначно.
Матрица квадратичной формы
Матрицей квадратичной формы называется матрица ее полярной билинейной формы.
Ранг квадратичной формы
Рангом квадратичной формы называют ранг ее матрицы в произвольном базисе.
(не) вырожденная квадратичная форма
Квадратичная форма называется вырожденной, если 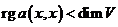 , и невырожденной, если
, и невырожденной, если 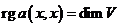 .
.
Свойства матрицы квадратичной формы
1) Матрица квадратичной формы симметрична
2) Любая квадратная симметричная матрица является матрицей единственной квадратичной формы в заданном базисе
3) При переходе от базиса к базису (матрица перехода ![]() ) матрица квадратичной формы изменяется следующим образом:
) матрица квадратичной формы изменяется следующим образом: ![]()
4) Пусть ![]() - произвольный фиксированный базис. Пусть квадратичная форма f(x) =
- произвольный фиксированный базис. Пусть квадратичная форма f(x) = ![]() имеет в этом базисе матрицу
имеет в этом базисе матрицу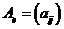 , а произвольный вектор x имеет в этом же базисе координаты (x1, x2, …, xn). Тогда результат действия квадратичной формы
, а произвольный вектор x имеет в этом же базисе координаты (x1, x2, …, xn). Тогда результат действия квадратичной формы ![]() на вектор x может быть записан в виде
на вектор x может быть записан в виде
f(x) = ![]() ,
,
или в более компактной форме:
f(x) = ![]()
где X =  - столбец координат вектора x в базисе e
- столбец координат вектора x в базисе e
4.4. Канонический вид квадратичной формы
Канонический вид квадратичной формы
Каноническим видом квадратичной формы называется ее запись, содержащая только квадраты переменных:
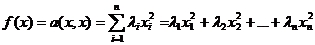 ,
,
Числа ![]() (некоторые из которых могут равняться нулю) называются каноническими коэффициентами квадратичной формы.
(некоторые из которых могут равняться нулю) называются каноническими коэффициентами квадратичной формы.
Очевидно, что количество ненулевых коэффициентов в каноническом виде квадратичной формы совпадает с ее рангом.
Канонический базис квадратичной формы
Базис ![]() называется каноническим базисом квадратичной формы f(x) = a(x, x),
называется каноническим базисом квадратичной формы f(x) = a(x, x),
если запись этой формы в этом базисе является канонической, то есть содержащей только квадраты переменных:
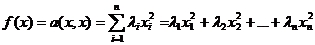
Это же определение на "матричном языке" звучит так:
Базис ![]() называется каноническим базисом квадратичной формы f(x) = a(x, x),
называется каноническим базисом квадратичной формы f(x) = a(x, x),
если матрица Ae этой формы в этом базисе имеет диагональный вид:
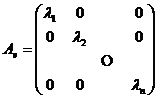 .
.
Метод Лагранжа (метод выделения полных квадратов)
Метод Лагранжа приведения квадратичной формы к каноническому виду путем выделения полных квадратов состоит из нескольких этапов.
1. Если в записи квадратичной формы присутствует слагаемое, содержащее квадрат хотя бы одной переменной (например, a11x12, причем a11 ≠ 0), сгруппировать все слагаемые с этой переменной (записать в одну скобку):
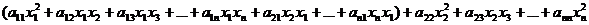
2. Вынести за скобки коэффициент ( ≠ 0) при квадрате этой переменной:
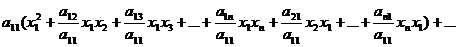
3.1. Записать квадрат следующего выражения, полученного из суммы в скобках делением на изначально выбранную переменную, а также делением всех слагаемых, кроме первого, на 2:
![]()
Замечание.
Если возвести в квадрат записанную сумму и умножить на коэффициент, вынесенный за скобки, то в результате получатся все слагаемые, содержащие переменную x1, входившие в запись квадратичной формы. Одновременно возникнут (и довольно много) слагаемые, не входившие в первоначальную запись квадратичной формы. Но все "новые" слагаемые не содержат переменной x1.
3.2.
Таким образом, запись квадратичной формы приобретает следующий вид:
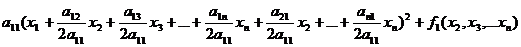 ,
,
где f1(x2, …, xn) – квадратичная форма, в записи которой не содержится переменной x1.
В дальнейшем шаги 1-3 повторяются до тех пор, пока в записи квадратичной формы не останутся только квадраты "скобок". Сделав замену переменных, при которой "первую скобку" обозначим через x1', вторую – через x2', и т. д., получим следующую запись квадратичной формы, слагаемые в которой содержат только квадраты переменных:
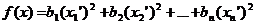
Замечание. Возможно, на каком-либо шаге запись квадратичной формы fk(xr+1, …, xn) не содержит квадрата ни одной переменной (а только произведения попарно различных переменных). В этом случае делается промежуточная замена:
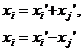
В результате такой замены слагаемое aijxixj, содержащее произведение переменных xi и xj, преобразуется в два слагаемых, уже содержащих квадраты переменных xi' и xj':
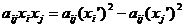
После чего можно приступать к выполнению этапа 1.
Теорема о существовании канонического базиса квадратичной формы. Метод Лагранжа.
Для любой квадратичной формы существует канонический базис. Метод Лагранжа выделения полных квадратов приводит к каноническому виду записи квадратичной формы за конечное число шагов.
Теорема о существовании ортонормированного канонического базиса (приведение к главным осям).
Для любой квадратичной формы в евклидовом пространстве существует ортонормированный базис, в котором она имеет канонический вид.
Формулы Якоби
Если в матрице квадратичной формы f(x) ранга ![]() первые
первые ![]() угловых миноров отличны от нуля:
угловых миноров отличны от нуля: 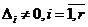 , то существует базис e, в котором матрица квадратичной формы имеет диагональный вид
, то существует базис e, в котором матрица квадратичной формы имеет диагональный вид 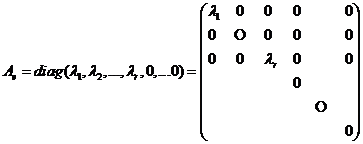
При этом канонические коэффициенты λi квадратичной формы связаны с угловыми минорами Δi следующими соотношениями:![]() ,
,
которые называются формулами Якоби.
Лекция № 8. Раздел 4. Билинейные и квадратичные формы.
Темы:
4.5. Индексы инерции квадратичной формы
4.6. Знакоопределенные и знакопеременные квадратичные формы
Билинейные и квадратичные формы
в вещественном (действительном) линейном пространстве.
4.5. Индексы инерции квадратичной формы
Индексы инерции квадратичной формы
Пусть квадратичная форма f(x) = ![]() приведена к какому-нибудь каноническому виду
приведена к какому-нибудь каноническому виду 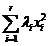 . Число
. Число ![]() положительных коэффициентов λi при квадратах переменных называют положительным индексом инерции, а число
положительных коэффициентов λi при квадратах переменных называют положительным индексом инерции, а число 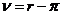 отрицательных коэффициентов λi называют отрицательным индексом инерции.
отрицательных коэффициентов λi называют отрицательным индексом инерции.
Сигнатура
Число ![]() называют сигнатурой квадратичной формы.
называют сигнатурой квадратичной формы.
Закон инерции
Положительный и отрицательный индексы инерции вещественной квадратичной формы не зависят от выбора канонического базиса.
Сигнатурное правило Якоби
Пусть в матрице квадратичной формы f(x) ранга ![]() первые
первые ![]() угловых миноров отличны от нуля:
угловых миноров отличны от нуля: ![]() . Тогда положительный индекс инерции
. Тогда положительный индекс инерции ![]() равен числу совпадений знаков в последовательности
равен числу совпадений знаков в последовательности ![]() , а отрицательный индекс инерции
, а отрицательный индекс инерции ![]() равен числу перемен знаков в этой последовательности.
равен числу перемен знаков в этой последовательности.
4.6. Знакоопределенные и знакопеременные квадратичные формы
Знакоопределенная квадратичная форма
Квадратичная форма называется положительно (отрицательно) определенной, если она принимает только положительные (отрицательные) значения на всех ненулевых векторах: (f(x) = ![]() > 0 (соответственно, < 0)
> 0 (соответственно, < 0) ![]() . Такие формы называют знакоопределенными.
. Такие формы называют знакоопределенными.
Знакопеременная квадратичная форма
Квадратичная форма, для которой существуют векторы ![]() и
и ![]() такие, что f(x) =
такие, что f(x) = ![]() > 0 и f(y) =
> 0 и f(y) =![]() < 0 называется знакопеременной.
< 0 называется знакопеременной.
Критерий знакоопределенности квадратичной формы
Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда ее положительный (соответственно, отрицательный) индекс инерции совпадает с размерностью пространства.
То есть, в любом каноническом виде положительно (отрицательно) определенной квадратичной формы в n-мерном пространстве
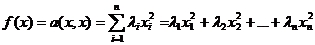
все коэффициенты λi положительны (отрицательны).
Следствие (об определителе положительно определенной квадратичной формы).
Определитель матрицы положительно определенной квадратичной формы положителен.
Критерий Сильвестра
Пусть в некотором базисе квадратичная форма f(x) = ![]() имеет матрицу
имеет матрицу ![]() . Рассмотрим ее угловые миноры:
. Рассмотрим ее угловые миноры:
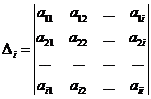
Квадратичная форма является положительно определенной тогда и только тогда, когда все ее угловые миноры положительны.
Квадратичная форма является отрицательно определенной тогда и только тогда, когда знаки ее угловых миноров чередуются, причем ![]() .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |





