11. Чему равна сумма чисел 2 и ? Запишите ответ.

12. Каких чисел больше – рациональных или иррациональных алгебраических?

13. Приведите пример иррационального числа, заключенного между числами и 0,3.

14. Какое действие, выполнимое на множестве действитель­ных чисел, не выполняется на множестве комплексных чисел?

Блок В (вопросы для контроля и самоконтроля методического характера)

1. Предложите вариант классификации множества комплексных чисел.

2. Что такое «решето Эратосфена»?

3. Какие числа называют числами-близнецами?

4. Какие элементы математического содержания исполь­зуются при изложении теории числа в курсе математики 5-6 классов?

5. Какой метод лежит в основе переноса свойств (законов) арифметических действий, сформулированных на множестве на­туральных чисел, на этапах расширения числовых множеств?

6. Какой математический аппарат используется для стро­гого обоснования существования квадратного корня из неотрицательного числа?

7. Какова мотивация расширения действительных чисел до множества комплексных чисел?

8. Как, согласно легенде, боги покарали ученика Пифагора, который разгласил тайну о несоизмеримости стороны и диагонали квадрата?

Вопросы для обсуждения на занятии:

1. Характеристика математической базы учащихся по курсу начальной школы.

2. Цели обучения линии числа в школьном курсе математики (основная, старшая школы).

3. Варианты логики построения теории числа в школьном курсе математики.

4. Мотивации практического и теоретического характера при расширении понятия числа.

5. Различные подходы к введению понятия «иррациональное число» в школьном курсе.

6. Варианты логики построения теории комплексных чи­сел в школьном курсе.

7. Роль геометрического материала при построении теории числа в курсе математики 5-6 классов. Конкретные примеры.

8. Понятие «вычислительная культура»:

- трактовка понятия;

- компоненты вычислительной культуры;

- этапы обучения математике, на которых возможна и целе­сообразна постановка цели «формирование вычислительной культуры»;

- примеры с разработкой соответствующей системы заданий.

Задания для подготовки к занятиям

1. Познакомьтесь с содержанием курса математики на­чальной школы и требованиями к математической подготовке учащихся начальной ступени обучения.

2. Опишите возможные варианты логики построения те­ории числа в школьном курсе математики (на основе анализа содержания линии числа в различных школьных учебниках).

3. Постройте классификацию множества комплексных чисел.

4. Как и в каком сочетании можно использовать в школе мотивации практического и теоретического характера при расширении понятия числа?

5. Какие возможны подходы к введению понятия «ирра­циональное число» в школьном курсе? (На основе анализа со­держания линии числа в различных школьных учебниках).

6. Какие возможны варианты построения теории комп­лексных чисел в школьном курсе? (На основе анализа содер­жания линии числа в различных школьных учебниках).

7. Свойства (законы) арифметических действий вводятся на множестве натуральных чисел. Какой метод лежит в основе пе­реноса этих свойств на этапах расширения числовых множеств?

8. Какова роль геометрического материала при постро­ении теории числа в курсе математики 5-6 классов? Приве­дите конкретные примеры.

9. Формирование математической культуры – одна из це­лей обучения математике. Вычислительная культура – один из компонентов общей математической культуры. Предложите ваш вариант трактовки понятия «вычислительная культура».

Выделите компоненты вычислительной культуры.

На каких этапах обучения математике, при обучении ка­кому содержанию возможна и целесообразна постановка цели «формирование вычислительной культуры»? Приведите конк­ретный пример с соответствующей системой заданий.

Составьте список литературы по вопросам развития поня­тия о числе для внеклассного чтения учащихся. Укажите, в каких классах она может быть использована.

Практическое занятие

Изучение десятичных дробей в 5-6 классах

Основные цели работы: выделить методические особенности в обучении теме «Десятичные дроби»; разработать методику изучения фрагментов содержания: «введение понятия», «вве­дение правила»; рассмотреть в практическом плане вопрос разработки системы контроля по теме.

Вопросы для повторения:

Блок А (вопросы для контроля и самоконтроля содержательного характера)

1.  Сформулируйте определение десятичной дроби.

2.  Какие из следующих чисел являются десятичными дробями: ; ; 9,04; 17,00; ?

3.  Какие общие сопутствующие понятия имеют место у де­сятичной и обыкновенной дробей?

4.  Какое теоретическое положение лежит в основе упрощения десятичной дроби:

3,2500 = 3,25?

5.  Может ли десятичная дробь быть неправильной?

6.  Можно ли при округлении десятичной дроби до сотых получить натуральное число?

Блок В (вопросы для контроля и самоконтроля методического характера)

Вопросы для обсуждения на занятии:

Задания для подготовки к занятиям:

Литература

1.  Aлександров П. С., Колмогоров числа // Вопросы преподавания математики в средней школе. – М.: Учпедгиз, 1961.

2.  Андронов для техникумов. – М.: Высшая школа, 1965.

3.  Методика преподавания математики в средней школе: Частные методики / Сост. и др. – М., 1985.

4.  Программы по математике для средней школы.

5.  Столяр математики. – Минск: Выш. школа, 1986.

6.  Фихтенгольц числа в средней школе / / Математическое просвещение. – М.: Гостехиздат, 1957. Вып. 2.

7.  Методика преподавания математики в средней школе: Частная методика: Учеб. пособие для студентов пед. ин-тов по физ. мат. спец./ , , и др.; Сост. . – М.: Просвещение, 1987.

8.  Методика преподавания математики в средней школе. Частные методики. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , и др. – М.: Просвещение, 1977.

9.  Газета «Математика» (приложение к газете «Первое сентября») за 2000–2009 гг.

10. Журнал «Математика в школе» 2000–2009 гг.

11. Учебники алгебры и алгебры и начал анализа разных автор­ских коллективов.

12. Методика преподавания математики в средней школе: Частная методика: Учеб. пособие для студентов пед. ин-тов по физ. мат. спец./ , , и др.; Сост. . – М.: Просвещение, 1987.

13. Методика преподавания математики в средней школе. Частные методики. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , и др. – М.: Просвещение, 1977.

14. Рогановский преподавания математики в средней школе: Учеб. пособие. – Мн.: Выш. шк., 1990.

15. , Тельгмаа –5, Математика–6, М.: Просвещение, 1998.

16. , Шарыгин –5, Математика–6, М.: Просвещение, 2000.

17. Алгебра: Учеб. для 7, 8 и 9 кл. сред. шк. / , , ; Под ред. .– М.: Просвещение, 2002.

18. , , Шварцбург : учеб. для 5 кл. общеобразоват. учреждений. – М.: Мнемозина, 2002.

19. , , Шварцбурд : Учеб. для 6 кл. общеобразоват. учреждений. – М.: Мнемозина, 2004.

20. Газета «Математика» (приложение к газете «Первое сентября») за 2003–2008 гг.

21. Статьи в журнале «Математика в школе»: Некоторые формы организации устного счета – №3, 1991; Индивидуальные задания для устранения ошибок – №5, 1993; Повышение вычислительной культуры учащихся – №5, 1995; О формировании навыков вычисления в уме – №5, 1987; О порядке выполнения действий – №2, 1965; Некоторые способы быстрых вычислений – №1, 1992; Еще раз о целых числах – №10, 2001; Задачи на умножение положительных и отрицательных чисел – №5, 1980; Как я ввожу отрицательные числа – №7, 2002; Формальное и интуитивное в процессе развития понятия числа – №4, 1994; «Положительные и отрицательные числа» в некоторых зарубежных учебниках – №5, 1964; О пропедевтике действий с отрицательными числами – №3, 1991; О введении понятия противоположного числа и правила вычитания рациональных чисел – №1, 1960; Алгебраическая пропедевтика при сложении дробей с разными знаменателями – №2, 1996; Повторение в игровой форме действий с дробями – №8, 2001; О порядке изучения обыкновенных и десятичных дробей – №4, 1995; Поработаем устно в начале урока –№10, 2000.

Практическое занятие

Модуль числа в курсе девятилетней школы

Основные цели работы: выделить содержание темы, ее мате­матические основы и место в обучении математике; система­тизировать знания студентов по методам решения математи­ческих задач, содержащих модуль.

Вопросы для повторения:

Блок А (вопросы для контроля и самоконтроля содержательного характера)

1. Для каких значений а выполняется равенство ?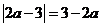

2. Докажите неравенство .

3. Решите уравнение .

4. Изобразите множество точек плоскости, координаты которых удовлетворяют неравенству .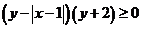

5. Постройте график уравнения .

Блок В (вопросы для контроля и самоконтроля методического характера)

1. На каких этапах обучения математике вводится опреде­ление модуля? В чем отличие этих определений?

2. Сформулируйте свойства модуля.

3. Какова, на ваш взгляд, причина рассмотрения уравне­ний и неравенств с модулем в теме «Неравенства» (по учебни­ку и др. «Алгебра-8»)?

4. Опишите математическим языком положение точки х на координатной прямой, если .

5. Приведите способы решения уравнения в соответствии с теорией, изложенной в теме «Нера­венства» (по учебнику и др. «Алгебра-8»). Каковы математические основы каждого из приведенных спо­собов?

6. Выполните те же задания для неравенства .

Задания для подготовки к занятиям

1. На основе анализа программ и школьных учебников по курсу математики 5-6 классов, алгебры, алгебры и начал анализа выделите:

- этапы обучения математике, на которых вводится опре­деление модуля;

- суть определений, их математические основы;

- свойства модуля, вводимые на протяжении обучения математике.

2. Выполните типологию задач по основным содержатель­ным линиям школьного курса математики, связанных с моду­лем (основание типологии – требование задачи).

3. Выделите аналитические методы решения алгебраиче­ских уравнений, содержащих неизвестное под знаком модуля. На конкретном наборе задач дайте иллюстрацию применения выделенных методов.

4. Выделите аналитические методы решения алгебраиче­ских неравенств, содержащих неизвестное под знаком моду­ля. На конкретном наборе задач дайте иллюстрацию примене­ния выделенных методов.

5. Выделите элементы теории преобразования графиков функций, содержащих аргумент под знаком модуля. Разрабо­тайте методику введения теории (на примере одного из преобра­зований). Приведите примеры задач, иллюстрирующих приме­нение введенной теории.

6. Методические особенности задач.

Для каждой из приведенных ниже задач определите место в учебном процессе; определите возможные функции в соот­ветствии с этапом обучения; разработайте вариант методики работы по поиску решения.

Задача 1. Упростите выражение .

Задача 2. Докажите, что для выполнения равенства 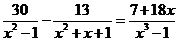необходимо, чтобы . Является ли это условие достаточным?

Задача 3. Решите уравнение .

Задача 4. Решите неравенства:

а) ; б) .

Задача 5. Изобразите на координатной плоскости область, задаваемую системой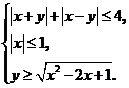

Вопросы для обсуждения на занятии:

1. Типология задач по основным содержательным линиям школьного курса математики, связанных с модулем (основа­ние типологии – требование задачи).

2. Аналитические методы решения алгебраических урав­нений, содержащих неизвестное под знаком модуля. Иллюст­рация применения выделенных методов.

3. Аналитические методы решения алгебраических нера­венств, содержащих неизвестное под знаком модуля. Иллюст­рация применения выделенных методов.

4. Преобразования графиков функций, содержащих аргу­мент под знаком модуля. Методика введения теории (на при­мере одного из преобразований). Примеры задач, иллюстри­рующих применение введенной теории.

Практические занятия

Методика преподавания геометрии

План: Пропедевтический курс геометрии. Пропедевтический курс геометрии. Составление конспекта урока по общепринятой схеме для 5-6-х классов по определенной теме. Изучение геометрического материала в 5-6 классах. Основные понятия и определения. Методика изучения геометрических фигур и их измерений в систематическом курсе геометрии. Изучение векторов и координат на плоскости. Логическое строение геометрии. Методика изучения аксиом. Взаимное расположение прямых на плоскости. Разработка конспекта урока «Решение задач на параллельность прямых». Виды многоугольников. Обобщающий урок по теме «Четырехугольники». Признаки равенства и подобия треугольников. Виды геометрических преобразований на плоскости: осевая и центральная симметрия, параллельный перенос, поворот, преобразования подобия. Методика изучения перпендикулярности прямых и плоскостей.

Литература

1. Методика преподавания математики в средней школе: Частная методика: Учеб. пособие для студентов пед. ин-тов по физ. мат. спец./ , , и др.; Сост. . – М.: Просвещение, 1987.

2. Методика преподавания математики в средней школе. Частные методики. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , и др. – М.: Просвещение, 1977.

3. Рогановский преподавания математики в средней школе: Учеб. пособие. – Мн.: Выш. шк., 1990.

4. Совайленко обучения математике в 5–6 классах. – М.: Просвещение, 1991.

5. Зильберберг математики: Подготовка и проведение: Кн. для учителя. – М.: Просвещение, 1995.

6. , , Шварцбург : учеб. для 5 кл. общеобразоват. учреждений. – М.: Мнемозина, 2002.

7. , , Шварцбурд : Учеб. для 6 кл. общеобразоват. учреждений. – 13-е изд., стереотип. – М.: Мнемозина, 2004.

8. Гусев -педагогические основы обучения математике. – М.: «Вербум-М», центр «Академия», 2003.

9. Методика обучения геометрии: Учеб. пособие для студ. высш. пед. учеб. заведений / , , и др.; Под ред. . – М.: Издательский центр «Академия», 2004.

10. Журнал «Математика в школе» 1991–2008 гг.

11. Газета «Математика» (приложение к газете «Первое сентября») за 2003–2008 гг.

Практические занятия

«Специфика восприятия и усвоения

алгебраического и геометрического материала в школе»

План: Особенности развития подростков и специфика обучения алгебре, связанная с ними. Специфика обучения алгебре как предмету. Объективные особенности геометрических представлений. Восприятие и усвоение геометрического пространства.

Литература:

1. Методика преподавания математики в средней школе: Общая методика. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , . – М.: Просвещение, 1980.

2. Методика преподавания математики в средней школе: Общая методика. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , и др.; Сост. , . – М.: Просвещение, 1985.

3. Темербекова преподавания математики: Учеб. пособие для студ. высш. учеб. заведений. – М.: Гуманит. изд. центр Владос, 2003.

4. Методика обучения геометрии: Учеб. пособие для студ. высш. пед. учеб. заведений / , , и др.; Под ред. . – М.: Издательский центр «Академия», 2004.

5. Саранцев обучения математике в средней школе: Учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / . – М.: Просвещение, 2002.

3. Рогановский преподавания математики в средней школе: Учеб. пособие. – Мн.: Выш. шк., 1990.

5. Геометрия, 7-9: Учеб. для общеоразоват. учреждений / , , и др. – М.: Просвещение, 2003.

7. Погорелов : Учеб. Для 7-11 кл. общеобразоват. учреждений. – М.: Просвещение, 1999.

8. Журнал «Математика в школе» 1991–2008 гг.

9. Газета «Математика» (приложение к газете «Первое сентября») за 2003–2008 гг.

Практические занятия

Тождественные преобразования в курсе математики средней школы,

методика их изучения

План: Различные подходы к определению тождества. Целенаправленность тождественных преобразований. Основные типы преобразований и этапы их изучения. Методические особенности изучения тождественных преобразований. Методика изучения тождественных преобразований трансцендентных выражений. Методические особенности работы по обучению теме «Тождественные преобразования выражений, содержащих квадратные корни».

Практическое занятие

Тождественные преобразования алгебраических выражений

Основные цели работы: познакомиться с содержанием линии «Тождественные преобразования алгебраических выражений» в школьном курсе математики и основами методики изучения содержания темы «Тождественные преобразования рацио­нальных выражений»»; рассмотреть пример организации само­стоятельной учебно-познавательной деятельности на уроках математики.

Вопросы для повторения:

Блок А (вопросы для контроля и самоконтроля содержательного характера)

1. Какое понятие более общее по отношению к понятию «тождество»?

2. Вычислите без калькулятора: а) 173· 227; б) 592; в) .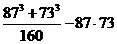

3. Зная, что , найдите значение выражения .

4. Упростите: .

5. Найдите значения а и , при которых выполняется ра­венство:

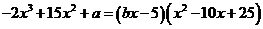. В ответ за­пишите сумму а и .

6. Найдите значение выражения , если известно, что .

Блок В (вопросы для контроля и самоконтроля методического характера)

1. Имеют ли место взаимосвязи линии тождественных преобразований с другими основными содержательными ли­ниями школьного курса математики? Если да, то с какими? Приведите примеры связей.

2. Перечислите возможные цели обучения линии «Тожде­ственные преобразования».

3. Является ли тождеством равенство в соответ­ствии с определением в учебнике:

а) «Алгебра - 8» и др.; б) «Алгебра – 9» и др.?

4. Выполняя задание на упрощение выражения, ученик оформил его так: 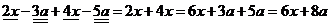. Какие ошибки допущены? Дайте версию причин их появления.

5. Выделите элементы теории тождественных преобразований, используемые при устном нахождении значения выражения .

Вопросы для обсуждения на занятии:

1. Этапы введения понятия тождества в курсе алгебры де­вятилетней школы. Методика введения понятия на каждом этапе (разработка фрагмента урока).

2. Методические особенности изучения темы «Одночлены и многочлены»:

- методика введения понятий;

- методика введения свойств степени с натуральным показателем;

- методика формирования умений и навыков по выпол­нению действий с одночленами (на примере умножения одно­членов).

3. Фрагменты методики обучения теме «Разложение мно­гочленов на множители».

Методика введения способов разложения многочленов на множители, включая применение тождеств сокращенного ум­ножения. При разработке методики исследуйте целесообраз­ность использования базовых знаний учащихся по линии числа; геометрической иллюстрации тождеств сокращенного умножения; разработки алгоритмических предписаний при формировании практических умений на первом этапе обуче­ния.

Дидактические функции и цели про ведения самостоя­тельных работ, требования к их организации, этапы формиро­вания навыка самостоятельной деятельности при обучении новому материалу. Разработайте систему самостоятельных работ обучающего характера по теме.

Система самостоятельных работ по теме обучающего характера.

Система промежуточного и итогового контроля по теме.

4. Варианты разрешения методической ситуации.

Ученики при выполнении преобразований допускают ошибки такого рода: а) ;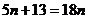

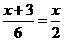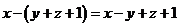б) ; в) ; г) .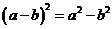

Причины этих ошибок, приемы их исправления. Пути предупреждения ошибок.

Задания для подготовки к занятиям

1. Проследите линию развития учения о тождественных преобразованиях в курсе математики средней школы на осно­ве анализа учебников алгебры и алгебры и начал анализа (в сравнительном плане рассмотрите учебники разных автор­ских коллективов).

2. Изучите программу по математике для девятилетней школы: содержание темы «Тождественные преобразования рациональных выражений», требования к умениям и навы­кам тождественных преобразований рациональных выраже­ний, планирование изучения темы.

3. Исследуйте вопрос о математических основах тождест­венных преобразований рациональных и дробно-рациональ­ных выражений по курсу математики 7-8 классов.

Дальнейшие задания выполните на основе учебников ал­гебры под редакцией .

4. Выполните логико-математический анализ теоретиче­ского содержания темы «Тождественные преобразования ра­циональных выражений» и методический анализ задачного материала.

5. Выделите этапы введения понятия тождества в курсе алгебры девятилетней школы. Разработайте методику введе­ния понятия на каждом этапе (разработка фрагмента урока).

Практическое занятие

Тождественные преобразования тригонометрических выражений

Основные цели работы: познакомиться с содержанием темы и логикой ее изложения в школьных учебниках; продолжить формирование умения выявлять внутренние и внешние связи изучаемого материала.

Вопросы для повторения:

Блок А (вопросы для контроля и самоконтроля содержательного характера)

1. К какому виду математических выражений относятся тригонометрические выражения?

2. Углом какой четверти является угол , если: а) ; б) ; в) ; г) ?

3. Определите знак произведения tg 2· sin 3· ctg 5· cos 1.

4. Какой знак имеет произведение sin х· cos х· tg х при: а) 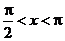; б) ?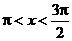

5. Существует ли такое значение х, при котором выполняется равенство cos х sin х = .

6. Упростите выражение: а) ; б)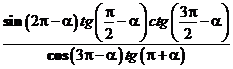

7. Вычислите: а) sin 1350 – sin 450; б) cos 750 + cos 150.

8. Вычислите tg х, если sin – cos = .

9. Вычислите , если .

10. Вычислите , если и .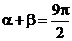

Блок В (вопросы для контроля и самоконтроля методического характера)

1. Цели изучения начального этапа тригонометрии «Три­гонометрические выражения и их преобразования» и требова­ния к математической подготовке.

2. Какие ведущие линии школьного курса математики яв­ляются базовыми для обучения теме? Приведите конкретные примеры.

3. Найдите все возможные способы решения задачи. В каж­дом способе выделите математическую основу и умения, кото­рыми должен владеть учащийся, чтобы задача была успешно решена.

Задача. Известно, что . Найдите значение выражения .

Вопросы для обсуждения на занятии:

1. Содержание темы и логика его изложения в учебниках разных авторских коллективов.

2. Вводная диагностическая работа (цель, содержание, функции задач, критерии оценки).

3. Вариант методики обучения:

- формулам приведения;

- теоремам сложения.

4. Вариант построения системы теоретических знаний по теме с ориентацией на решение задач.

5. Тригонометрический круг – средство формирования пропедевтических знаний по курсу тригонометрии.

6. Система задач, выполняющих пропедевтические функ­ции по функциональной линии и линии уравнений и нера­венств.

Задания для подготовки к занятиям

1. Сформулируйте цели начального этапа изучения триго­нометрии «Тригонометрические выражения и их преобразова­ния» и требования к математической подготовке (по програм­ме по математике для общеобразовательных учреждений).

2. Познакомьтесь с содержанием темы и логикой его изложения в учебниках разных авторских коллективов.

3. Какие ведущие линии школьного курса математики яв­ляются базовыми для обучения теме? Приведите конкретные примеры.

4. Разработайте вариант вводной диагностической рабо­ты, цель которой – актуализация базовых знании и определе­ние степени готовности учащихся к изучению новой темы.

5. Продумайте вариант построения системы теоретических знаний по теме с ориентацией на решение задач. Устано­вите связи между элементами этой системы.

4. Определите роль тригонометрического круга при обуче­нии теме. Сформулируйте определение тригонометрического круга, исследуйте возможность использования тригонометри­ческого круга в формировании пропедевтических знании по тригонометрии (линии функции, уравнений и неравенств). Разработайте систему задач, выполняющих пропедевтические функции по выделенным линиям.

Литература

1. Методика преподавания математики в средней школе: Частная методика: Учеб. пособие для студентов пед. ин-тов по физ. мат. спец./ , , и др.; Сост. . – М.: Просвещение, 1987.

2. Методика преподавания математики в средней школе. Частные методики. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , и др. – М.: Просвещение, 1977.

3. Рогановский преподавания математики в средней школе: Учеб. пособие. – Мн.: Выш. шк., 1990.

4. Мордкович . 7, 8, 9 кл.: В двух частях. Ч. 1: Учеб. для общеоб­ра­зоват. учреждений. – М.: Мнемозина, 2003.

5. Алгебра: Учеб. для 7, 8, 9 кл. сред. шк. / , , ; Под ред. .– М.: Просвещение, 2002.

6. Газета «Математика» (приложение к газете «Первое сентября») за 2003–2008 гг.

7. Журнал «Математика в школе» 1990–2008 гг.

Практические занятия

Методика изучения функций в девятилетней школе

План: Методика изучения функции. Развитие понятия функции. Функционально-графическая линия в учебниках алгебры . Методические особенности изучения линейной функции. Квадратичная функция. Степенная функция.

Литература:

1. Методика преподавания математики в средней школе: Частная методика: Учеб. пособие для студентов пед. ин-тов по физ. мат. спец./ , , и др.; Сост. . – М.: Просвещение, 1987.

2. Методика преподавания математики в средней школе. Частные методики. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , и др. – М.: Просвещение, 1977.

3. Рогановский преподавания математики в средней школе: Учеб. пособие. – Мн.: Выш. шк., 1990.

4. Мордкович . 7, 8, 9 кл.: В двух частях. Ч. 1: Учеб. для общеоб­ра­зоват. учреждений. – М.: Мнемозина, 2003.

5. Алгебра: Учеб. для 7, 8, 9 кл. сред. шк. / , , ; Под ред. .– М.: Просвещение, 2002.

6. Газета «Математика» (приложение к газете «Первое сентября») за 2003–2008 гг.

7. Журнал «Математика в школе» 1990–2008 гг.

2.  Рекомендуемая литература

Основная литература:

1.  Темербекова преподавания математики: учеб. пособие для студ. вузов, обуч. по спец. 032100 "Математика" / – М.: ВЛАДОС, 2003.

2.  Новые педагогические и информационные технологии в системе образования: Учеб. пособие для студ. пед. вузов и системы повыш. квалиф. пед. кадров / , , ; Под ред. . – М.: Издательский центр «Академия», 2008.

3.  Методика обучения геометрии: Учеб. пособие для студ. высш. пед. учеб. заведений / , , и др.; Под ред. . – М.: Издательский центр «Академия», 2004.

4.  Современные педагогические и информационные технологии в системе образования: учеб. пособие для студ. Вузов / , – М.: Академия, 2007.

5.  Газета «Математика» (приложение к газете «Первое сентября») за 2000–2013 гг.

6.  Журнал «Математика в школе» 2000–2013 гг.

Дополнительная литература:

1.  Методика преподавания математики в средней школе: Частная методика: Учеб. пособие для студентов пед. ин-тов по физ. мат. спец./ , , и др.; Сост. . – М.: Просвещение, 1987.

2.  Методика преподавания математики в средней школе. Частные методики. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , и др. – М.: Просвещение, 1977.

3.  Методика и технология обучения математике. Курс лекций: пособие для вузов / под науч. ред. , . – М.: Дрофа, 2005.

4.  Методика и технология обучения математике. Лабораторный практикум: учеб. пособие для студентов матем. факультетов пед. университетов / под науч. ред. . – М.: Дрофа, 2007.

5.  Саранцев обучения математике в средней школе: Учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / . – М.: Просвещение, 2002.

6.  Рогановский преподавания математики в средней школе: Учеб. пособие. – Мн.: Выш. шк., 1990.

7.  Виноградова преподавания математики в средней школе: учеб. пособие для студ. вузов / – Ростов н/Д: Феникс, 2005.

8.  Загвязинский обучения: Современная интерпретация: Учеб пособие для студ. высш. пед. учеб. заведений. – М.: Издательский центр «Академия», 2001.

9.  Мордкович . 9 кл.: В двух частях. Ч. 1: Учеб. для общеоб­ра­зоват. учреждений. – М.: Мнемозина, 2003.

10.  Алгебра: Учеб. для 9 кл. сред. шк. / , , ; Под ред. . – М.: Просвещение, 2002.

11.  Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. /, , и др.; Под ред. . –М.: Просвещение, 1994.

12.  Мордкович и начала анализа. 10-11 кл.: В двух частях. Ч.1: Учебник для общеобразоват. учреждений. – М.: Мнемозина, 2005.

13.  Атанасян : Учеб. для 7-9 кл. сред. шк. / , , и др. – М.: Просвещение, 2003.

14.  Геометрия: Учеб. для 10-11 кл. сред. шк./ , , и др. – М.: Просвещение, 1992.

15.  Погорелов : Учеб. Для 7-11 кл. общеобразоват. учреждений. – М.: Просвещение, 1999.

16.  Зильберберг математики: Подготовка и проведение: Кн. для учителя. – М.: Просвещение, 1995.

17.  Карп уроки математики. – М.: Просвещение, 1992.

18.  Волович обучать / Технология преподавания математики. – М.: LINKA-PRESS, 1995.

19.  Груденов методики работы учителя матема­тики: Кн. для учителя. – М.: Просвещение, 1990.

20.  Далингер реализации внутрипредметных связей при обу­чении математике: Кн. для учителя – М.: Просвещение, 1991.

21.  , Сохор и техника урока в школе: В по­мощь начинающему учителю. - М.: Просве­щение, 1985.

22.  Никольский и начала анализа: Учеб. для 10 кл. общеобра­зоват. учреждений / , , . – М.: Просвещение, 2001.

23.  Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. /, , и др. – М.: Просвещение, 1993.

24.  Башмаков и начала анализа: Учеб. для 10-11 кл. сред. шк. – М.: Просвещение, 1993.

25.  Дорофеев и начала анализа. 10 кл.: Учеб. для общеобразоват. учреждений: В 2 ч. Ч.1. /, , . – М.: Дрофа, 2003.

26.  и др. Геометрия: Учеб. для 7-11 кл. общеобразоват. учреждений. / , , . – М.: Просвещение, 1994.

27.  Геометрия: учебное пособие для 6 – 8 классов сред. шк. /, , ; Под ред. . – М.: Просвещение 1981.

3.  Перечень видео - и аудиоматериалов программного обеспечения

Цифровые образовательные ресурсы по математике

Учебные материалы //

http://school-collection. *****/catalog/pupil/?subject=16

Конспекты разработок уроков по избранным темам школьной программы по математике //

http://school-collection. *****/catalog/rubr/fd39f4a9-db7f-cb04-9acbf47e2/

Словарь-справочник понятий и фактов элементарной математики //

http://school-collection. *****/catalog/rubr/637182ba-dacb-8e36-95ade44/

Электронная библиотека учебно-методической литературы по математике //

http://school-collection. *****/catalog/rubr/696f5fc4-7f5c-b610-713f-014b7f9c0bc8/

4.  Примерные зачетные тестовые задания

1 вариант	2 вариант
1. Натуральные числа изучаются в: а) 7 классе, б) 6 классе, в) 5 классе, г) Не изучаются в школе. 2. Найти сумму корней уравнения: а) 6, б) 8, в) 64, г) 12. 3. Найти сумму всех трехзначных чисел, делящихся на 7. а) 6767, б) 70336, в) 4321, г) 9876. 4. Найти зная, что а) -1; 6, б) 7; 8, в) 9, г) 4,5	1. Логарифмическая функция изучается в: а) 9 классе, б) 10 классе, в) 11 классе, г) Не изучается в школе. 2. Решить уравнение а) -0,5; 2; -1, б) 0; 1; -0,5, в) 6: 0; -1, г) 0,5; 1; 2. 3. Найти сумму всех трехзначных чисел, делящихся на 13. а) 54321, б) 37674, в) 7659, г) 43679. 4. Найти , зная, что а) 0, б) 0,5, в) 1, г) 0,6.

5. Примерный перечень вопросов к экзамену

1. Цели обучения математике в школе. Значение школьного курса математики в общем образовании. Содержательные линии школьного курса математики. Анализ программ для 5-11 классов.

2. Принципы дидактики в обучении математике.

3. Научные методы обучения математике.

4. Репродуктивные и продуктивные методы обучения математике. Применение проблемного обучения, программированного обучения, ЭВМ в обучении математике.

5. Математические понятия и методика их формирования.

6. Аксиомы и теоремы, методика их изучения.

7. Роль задач в обучении математике. Методика работы над текстовой задачей.

8. Формы организации урока математики. Типы уроков, их структура. Основные требования к уроку. Уроки-лекции, семинары, практикумы, зачет.

9. Планирование работы учителя. Подготовка учителя к уроку.

10. Организация самостоятельной деятельности учащихся. Проверка знаний учащихся,

нормы оценок.

11. Средства обучения математике.

12. Особенности преподавания математики в школах и классах с углубленным изучением математики.

13. Методика работы над геометрической задачей.

14. Индивидуализация и дифференциация процесса обучения.

15. Методика изучения темы «Натуральные числа».

16. Методика изучения темы «Обыкновенные дроби».

17. Методика изучения темы «Десятичные дроби».

18. Методика изучения положительных и отрицательных чисел в школьном курсе математики.

6. Примерная тематика рефератов

1. Использование современных информационных и коммуникационных технологий в учебном процессе.

2. Аудиовизуальные технологии обучения математики.

3. Технологический подход к обучению математике.

4. Индивидуализация обучения математике.

5. Технология использования индивидуализированной системы задач при обучении математике.

6. История развития понятия числа.

7. Система мер и способы измерения величин.

8. Геометрия – от Евклида до наших дней.

9. Методы устных вычислений.

7.  Работа с тестовой системой курса

База тренировочных тестовых заданий по курсу ТиМОМ выложена в «Системе управления обучением факультета ФМОИиП МГГУ» в категории «Математика с дополнительной специальностью Информатика» в блоке «Теория и методика обучения математике».

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3