Методические рекомендации по изучению дисциплины «Теория и методика обучения математике» (стр. 2 )

1.  Тематика и планы аудиторной работы студентов по изученному материалу

(планы последовательного проведения занятий: ПР, СМ, ЛБ)

Практические занятия

«Общие вопросы теории и методики обучения математике»

План: Предмет и методы теории методики обучения математике, цели и содержание школьного курса математики. Анализ программ и учебников по математике средней школы, гимназий. Методы и средства обучения математике. Математические предложения, задачи в обучении математике, типы уроков. Составление конспекта урока. Принципы дидактики в обучении математике, математические понятия, углубленное изучение математики, внеклассная работа по математике, индивидуализация и дифференциация процесса обучения.

Практическое занятие

Логико-математический анализ определений понятий,

основные этапы формирования понятий

Основные цели работы: сформировать умения выполнять логико-математический анализ определений понятий школьного курса, показать на примерах возможную методику организации работы на основных этапах формирования понятий.

Вопросы для обсуждения на занятиях

1.  Понятие. Объем и содержание понятия.

2.  Структура определения. Логико-математический анализ определений.

3.  Процесс формирования понятий.

4.  Варианты методики введения понятий школьного курса математики.

Задания для подготовки к занятиям

1.  Вспомните основной теоретический материал темы.

2.  Выполните классификацию понятия «комплексные числа».

3.  Для понятий «отрезок» и «арифметический квадратный корень»:

- установите способ определения;

- определите структуру определения;

- разработайте методику введения дедуктивным и индуктивным путями.

4.  На основе анализа школьных учебников по математике 5-6 классов установите возможные последовательности изучения множества рациональных чисел.

5.  Для приведенных в списке понятий школьного курса математики установите вид (способ) определения, определите структуру определения (род, термин, видовые отличия, вид
логических связей видовых отличий) понятий, которые определены через ближайший род и видовые отличия.

Список понятий: десятичная дробь; обыкновенная дробь; равные дроби; мод-6 кл.); тождество; модуль числа; арифметическая (геометрическая) прогрессия («Алгебра», 7-9 кл.): точка; прямая; параллелограмм; прямоугольник: ромб; квадрат; симметрия относительно точки; параллельный перенос; скрещивающиеся прямые; параллельность прямой и плоскости («Геометрия, 7-11 кл.).

6.  Разработайте методику введения дедуктивным и индуктивным путями трех понятий по одному из школьных курсов: «Математика», 5-6 кл., «Алгебра», 7-9 кл., «Геометрия», 7-9 кл. (выбор понятия осуществляет студент).

Методический комментарий к заданиям

Понятие – целостная многоуровневая иерархически организованная структура, включающая образы разной степени обобщенности.

Математические понятия отражают в нашем мышлении определенные формы и отношения действительности, абстрагированные от реальных ситуаций.

Понятие характеризуется: объемом; содержанием (характеристическое свойство (свойства), присущее всем объектам класса).

Средством раскрытия объема понятия является классификация. В качестве примера выполним классификацию понятия «четырехугольник».

Классифицируя далее понятие «параллелограмм», можно в качестве основания классификации взять отношение длин смежных сторон и тем самым выделить из множества параллелограммов множество ромбов. Если же в качестве основания взять наличие прямого угла, то можно выделить множество прямоугольников. Множество квадратов будет пересечением множества ромбов и прямоугольников (заметим, что на этом шаге нарушен один из научных принципов проведения классификации, но, учитывая потребность решения задач, эту взаимосвязь между частными видами параллелограмма целесообразно показать).

Содержание понятия раскрывается с помощью определения.

Виды определений: вербальные и невербальные (остенсивные). Вербальные в свою очередь делятся на явные (родовидовые) и неявные (аксиоматические и описательные). Неявно определяются исходные понятия; например, в курсе геометрии таковыми являются понятия точки, прямой.

Структура явного определения: термин – род – видовые отличия.

Видовые отличия могут быть заданы разными способами, например: описанием, отрицанием, конструктивно, рекурсивно.

Таким образом, можно конкретизировать виды определений через ближайший род и видовые отличия, выделив определение понятия посредством указания характеристических свойств: конструктивные; рекурсивные; определения-отрицания.

Видовые отличия, выделенные в определении, могут быть связаны конъюнктивно и дизъюнктивно. С учетом вида логической связи видовых отличий выделяют конъюнктивные и дизъюнктивные определения.

Примеры выполнения логико-математического анализа

родовидового определения понятия

Пример 1. Определение неправильной дроби.

Дробь, в которой числитель больше знаменателя или равен ему, называется неправильной дробью.

Термин – неправильная дробь; род – дробь; видовые отличия – числитель больше знаменателя, числитель равен знаменателю.

Видовые отличия соединены дизъюнктивно.

Вывод: определение неправильной дроби вербальное, дизъюнктивное.

Пример 2. Определение параллельных прямых.

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Термин – параллельные прямые; род – пары прямых; видовые отличия – лежат в одной плоскости, не пересекаются.

Видовые отличия соединены конъюнктивно.

Вывод: определение параллельных прямых вербальное, конъюнктивное.

Процесс формирования понятий у человека включает следующие этапы: перцепт (образ восприятия) – представление (вторичный образ – создается у ученика в отсутствии наглядной основы) – предпонятие (образный концепт – ученик имеет образы, адекватные понятию, может назвать свойства
объектов, существенные для понятия, но не может выделить их достаточный набор, может не владеть кванторами) – понятие (мыслится в системе понятий).

Определить объект – значит выбрать из его существенных свойств такие и столько, чтобы каждое из них было необходимо, а все вместе достаточны для отличия определяемого объекта от других. Существует два подхода к введению понятия и определения понятия: дедуктивный и индуктивный.

Методика обучения математике выделяет основные этапы обучения явным определениям (раскрытия содержания математического объекта):

1.  логический анализ структуры определения объекта (термин, род, видовые отличия, их логическая связь);

2.  действие «подведение под понятие (решение задачи на «распознавание» – выделение математического объекта среди предложенных);

3.  действие получения следствий из факта, что конкретный объект принадлежит к классу объектов, охарактеризованных определением;

4.  если требует педагогическая ситуация, замена определения ему эквивалентным.

Практическое занятие

Методика обучения правилам и алгоритмам

Основные цели работы: сформировать умения выполнять логико-математический анализ правил школьного курса, разрабатывать алгоритмические предписания; раскрыть методику на основных этапах работы: по введению правил и их применению; по обучению решению алгоритмических задач.

Вопросы для обсуждения на занятиях

1.  Теоретический материал по теме «Алгоритмы, методика обучения правилам и алгоритмам».

2.  Варианты логико-математического анализа правил.

3.  Варианты разработки алгоритмических предписаний.

Задания для подготовки к занятиям

1. Выделите основные теоретические положения по теме «Алгоритмы. Методика формирования алгоритмов в школьном курсе математики» по материалам лекции.

2. Выполните логико-математический анализ приведенных ниже правил по курсу математики 5-6 классов. Если правило не является алгоритмом, то разработайте соответствующий алгоритм.

Правило умножения десятичных дробей: «Чтобы умножить десятичную дробь на десятичную дробь, надо выполнить умножение, не обращая внимания на запятые. И в результате справа отделить запятой столько знаков, сколько их в обоих множителях вместе».

Правило выделения целой части из неправильной дроби: «Чтобы из неправильной дроби выделить целую часть, надо: разделить с остатком числитель на знаменатель; неполное частное будет целой частью; остаток (если он есть) дает числитель, а делитель – знаменатель дробной части».

Правило деления дроби на дробь: «Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю».

3. Разработайте алгоритм решения задачи нахождения наименьшего общего кратного двух чисел.

4. Разработайте алгоритм (памятку):

- разложения многочлена на множители способом вынесения общего множителя за скобки;

- разложения многочлена на множители способом группировки;

- решения квадратного уравнения.

Методический комментарий к заданиям

Алгоритмы являются элементами теоретических знаний, с которыми учащиеся встречаются наряду с определениями понятий и математическими утверждениями (аксиомами, теоремами).

Понятие алгоритм – основное, неопределяемое. Сущность его на содержательно-интуитивном уровне может быть описана следующим образом: алгоритм – понятное предписание, указывающее, какие операции и в какой последовательности необходимо выполнить с данными, чтобы решить задачу определенного типа.

Свойства алгоритмов:

1. массовость (возможность использования для любой задачи данного типа);

2. элементарность и дискретность шагов (отдельные законченные шаги, каждый из которых в состоянии выполнить исполнитель);

3. детерминированность (однозначность определения первого и каждого следующего шагов, т. е. процесс решения задачи строго направлен);

4. результативность (точное выполнение указаний при решении задачи всегда приведет к результату, т. е. к получению математического факта).

Одна из основных линий курса математики 5-6 классов – линия числа. На первом этапе обучения какой-либо операции на числовом множестве формулируется правило. Правило – это свернутый алгоритм. Обычно в правиле выделяются блоки – отдельные шаги (системы операций в сжатом виде, некоторые операции вообще не содержатся в формулировке правила). Это,
в основном те операции, которые необходимы на начальном этапе применения правила и отработаны до введения правила.

Можно утверждать, что любой алгоритм – правило; однако, не всякое правило является алгоритмом.

Логико-математический анализ правил (алгоритмов)

Логический анализ предполагает:

- проверку наличия характеристических свойств алгоритма;

- выделение последовательности операций и логических условий;

- установление связей с другими знаниями.

Математический анализ – установление математической основы, т. е. базовых математических положений. Если в результате логико-математического анализа правила учитель убеждается в том, что правило не является алгоритмом, то целесообразно (с учетом уровня подготовленности учащихся класса) разработать предписание выполнения того или иного действия, понятное каждому ученику. Также целесообразно проводить работу в этом направлении при обучении алгебре, алгебре и началам анализа. Основой разработки предписаний может служить, например, типовая задача темы «Тождественные преобразования», решение уравнения определенно
го типа и т. д. Если на начальной стадии обучения к составлению алгоритмов желательно привлекать учащихся по мере возможности, то в старших классах это делать необходимо с целью формирования определенного исследовательского умения, именно умения открывать общий метод.

Выделяются следующие основные этапы работы по введению правил, их применению и по обучению решению алгоритмических задач:

- выполнение учителем логико-математического анализа правила;

- разработка алгоритмического предписания (в случае необходимости);

- разработка и проведение этапа актуализации знаний, необходимых для обоснования необходимости и введения алгоритма;

- введение алгоритмического предписания (обучающий этап);

- этап закрепления (применение введенного алгоритма при решении типовых задач).

Пример. Рассмотрим методику введения правила деления дроби на дробь: «Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю». Проводим
логико-математический анализ этого правила.

Цель введения правила: сформировать умение выполнять деление дробных чисел.

1. Данное правило – не алгоритм, так как не обладает свойствами алгоритма, а именно:

- свойством массовости (правило не является руководством для выполнения деления на натуральное число, деления смешанных чисел);

- свойством элементарности и дискретности (не выделены отдельные и законченные шаги);

- свойством детерминированности (не определен первый шаг, нет строгой направленности процесса выполнения действия);

- свойством результативности (так как не обладает ни одним из указанных выше свойств).

2. Логические условия определения делимого, делителя и числа, обратного данному.

3. Базовые знания: понятие дроби; дробного числа; числа, обратного данному. Умения: выполнять преобразования дробных чисел (преобразование смешанного числа в неправильную дробь, обратное преобразование); при менять правило умножения дробей; упрощать дробь (сокращение дроби).

Далее разрабатываем алгоритм.

Разрабатывать алгоритмическое предписание можно двумя путями: сформулировать алгоритм для нахождения частного двух дробей и затем на примерах показать его применение к частным случаям деления натурального числа на дробь и дроби на натуральное число, деления смешанных чисел; частные случаи сразу включать в рассмотрение.

Первый путь. Алгоритмическое предписание деления дроби на дробь: .

1.  Определите делимое .

2.  Определите делитель .

3.  Найдите дробь, обратную делителю .

4.  Делимое умножить на число, обратное делителю по правилу умножения дроби на дробь .

5.  Если возможно, полученную дробь упростите (сократите), выделите целую часть.

6.  Запишите ответ.

Частные случаи:

- если делимое или делитель – целое число, то, прежде чем приступать к выполнению предписания, представить его в виде дроби со знаменателем единица ;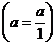

- если хотя бы один из компонентов действия – смешанное число, выразить его в виде дробного числа .

Второй путь. Рассмотрим другой вариант оформления алгоритмического предписания.

Необходимо выполнить систему подготовительных упражнений:

- сократите дроби: ; ;

- исключите целую часть: ; ;

- замените неправильной дробью: ; ;

- найдите произведение дробей: ; ; ;

- найдите число, обратное данному: ; ; ; ;

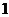- умножьте: на число, обратное ; на число, обратное .

На этапе введения алгоритмического предписания необходимо при выполнении заданий на нахождение частного дробных чисел каждый шаг выполнять в соответствии с предписанием (постоянно работать с ним). При рассмотрении частных случаев также следует обращаться к предписанию.

При обучении алгебре на первоначальном этапе потребность в разработке алгоритмов не уменьшается.

Пример алгоритмического предписания решения типовой задачи разложения на множители по формуле разности квадратов с рассмотрением примеров решения задач указанного типа. Условно назовем такого рода предписания памятками.

Памятка по разложению многочлена на множители

по формуле разности квадратов :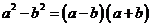

1.  Убедитесь, что данное выражение является разностью.

2.  Назовите выражения, составляющие эту разность.

3.  Проверьте, можно ли представить эти выражения в виде квадратов.

4.  Если выражения, составляющие разность, представимы в виде квадратов, то разложите данную разность на множители по формуле разности квадратов.

Пример 1. Разложите на множители многочлен .

1.  Данное выражение является разностью: .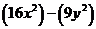

2.  Уменьшаемое: , вычитаемое: .

3.  Проверим, можно ли представить уменьшаемое и вычитаемое в виде квадратов:

, аналогично: .

4.  Разложим многочлен на множители по формуле разности квадратов:

.

Вывод: .

Пример 2. Разложите на множители многочлен .

Данное выражение является разностью: .

Уменьшаемое: , вычитаемое: .

Проверим, можно ли представить уменьшаемое и вычитаемое в виде квадратов:

и .

Вычитаемое представить в виде квадрата нельзя.

Вывод: многочлен разложить на множители по формуле разности квадратов нельзя.

Математические утверждения. Теорема.

Работа с теоремой, ее доказательством при обучении математике

Задания

1. Выполнить логико-математический анализ утверждений, им обратных, противоположных и обратных противоположным.

Утверждение 1. В равнобедренном треугольнике углы при основании равны.

Утверждение 2. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Вертикальные углы равны.

Утверждение 4. Если запись натурального числа оканчи­вается цифрой 0 или 5, то число делится на 5.

2. Выполните логико-математический анализ четырех ут­верждений школьного курса математики (два по геометрии и два по алгебре), а также утверждений, обратных данным, противоположных данным, противоположных обратным. Утверждения выберите самостоятельно.

3. Выделите общие методические рекомендации по обучени­ю теоремам (по материалам лекции).

4. Разработайте методику обучения теоремам.

Теорема 1. Если обе части неравенства умножить на одно то же отрицательное число, то знак неравенства изменится на противоположный.

Теорема 2. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Комментарий к заданиям

Суждения – это предложения, в которых выражена мысль о предмете, объекте, явлении.

Два основных свойства суждений:

- суждение что-то отрицает или утверждает;

- суждение является истинным или ложным.

Структура суждения:

- логическое подлежащее (субъект мысли);

- логическое сказуемое (предикат мысли);

- логическая связка.

Виды суждений:

- общеутвердительное;

- частно утвердительное;

- общеотрицательное;

- частно отрицательное.

Логическое предложение, выражающее суждение о матема­тических объектах, называется математическим предложе­нием. Каждая математическая теория представляет собой мно­жество математических предложений, описывающее какую-то структуру или какой-то аксиоматизируемый класс структур.

Принадлежность предложения к некоторой математиче­ской теории определяется двумя признаками:

- предложение сформулировано или записано на языке данной теории, состоит из математических и логических (при­надлежащих языку теории) терминов или символов и не содержит никаких других терминов или символов;

- предложение истинно, оно или является исходным ис­тинным предложением (аксиомой), или истинность предложе­ния устанавливается доказательством с помощью исходных или ранее доказанных истинных предложений.

Например, предложение «Сумма углов треугольника рав­на 1800» - геометрическое, принадлежит теории евклидовой геометрии, потому что оно сформулировано на языке геомет­рии, состоит из геометрических терминов (сумма углов, тре­угольник, 1800) и логических терминов (всякого, равна); его истинность доказывается в рамках евклидовой геометрии.

Раскрыть логическую структуру математического предло­жения – значит показать, из каких элементарных предложе­ний оно сконструировано и как составлено, т. е. с помощью ка­ких и в каком порядке применяемых логических связок. (Логи­ческие связки наиболее часто используемые: «не», «и», «или», «если... , то», «тогда и только тогда», «существует» и т. д.) Ма­тематические предложения бывают простые и сложные.

Теорема – математическое предложение, истинность ко­торого установлена с помощью доказательства.

Действие «анализ математического утверждения (теоремы)» предусматривает выделение:

- разъяснительной части;

- условия;

- заключения;

- логических связок;

- установление вида (простое или сложное).

Выделяют две формы формулирования теоремы: импликативную и категоричную.

Пример. Выполнить анализ математического утвержде­ния: «Сумма смежных углов равна 1800», а также утверждени­й: обратного данному, противоположного данному и противоположного обратному.

1.  Утверждение сформулировано в категоричной форме.

2.  Целесообразно утверждение переформули­ровать, используя импликативную форму:

Данное утверждение (1): «Если углы смежные, то их сумм­а равна 1800».

3.  Утверждение, обратное данному (2): «Если сумма двух уг­лов равна 1800, то углы смежные».

4.  Утверждение, противоположное данному (3): «Если углы не смежные, то их сумма не равна 1800».

5.  Утверждение, обратное противоположному (4): «Если сумма двух углов не равна 1800, то углы не смежные».

Анализ математического утверждения «Сумма смежных углов равна 1800».

Термин «математическое доказательство» предусматривает доказательство предложений в рамках какой-либо математической теории. Различают содержательные (неформальные) и формальные доказательства, которые применяют­ся соответственно в содержательных (неформальных или по­луформальных) и в формальных математических теориях.

В школьном обучении некоторые начальные фрагменты математических теорий излагаются неформально (алгебра, геометрия, анализ).

Можно сказать, что курс «Математика 5-6» относится в целом к теории, изложенной на содержательном уровне, т. е. в нем используются обычные рассуждения, а правила логиче­ского вывода не фиксируются. Принципиально иной при­мер – курс геометрии.

Разделяют виды доказательств: прямое (например, син­тетическое) и косвенное (например, методом от противного).

Вариант методики обучения построению прямого доказа­тельства

на начальном этапе обучения геометрии.

Задача. Даны: прямая а и точки А, В, С, не лежащие на прямой а. Известно, что отрезок АВ пересекает прямую а, а отрезок АС не пересекает ее. Пересекает ли прямую а отре­зок ВС? Ответ обоснуйте.

Литература

1.  Методика преподавания математики в средней школе: Общая методика. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , . – М.: Просвещение, 1980.

2.  Методика преподавания математики в средней школе: Общая методика. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / , , и др.; Сост. , . – М.: Просвещение, 1985.

3.  Темербекова преподавания математики: Учеб. пособие для студ. высш. учеб. заведений. – М.: Гуманит. изд. центр Владос, 2003.

4.  Методика обучения геометрии: Учеб. пособие для студ. высш. пед. учеб. заведений / , , и др.; Под ред. . – М.: Издательский центр «Академия», 2004.

5.  Саранцев обучения математике в средней школе: Учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / . – М.: Просвещение, 2002.

6.  Алгебра: Учеб. для 7, 8 и 9 кл. сред. шк. / , , ; Под ред. .– М.: Просвещение, 2002.

7.  , Тельгмаа –5, Математика–6, – М.: Просвещение, 1998.

8.  , , Математика–5, Математика–6, – М.: Просвещение, 2000.

9.  Атанасян : Учеб. для 7-9 кл. сред. шк. / , , и др. – М.: Просвещение, 2003.

10.  Журнал «Математика в школе» 1991–2008 гг.

11.  Газета «Математика» (приложение к газете «Первое сентября») за 2003–2008 гг.

Практические занятия по теме «Линия числа в школьном курсе математики»

План: Расширение понятия числа. Методика изучения натуральных чисел. Дробные числа. Изучение обыкновенных и десятичных дробей. Положительные и отрицательные числа, действия над ними. Действительные числа, методика их изучения и действий над ними.

Практическое занятие

Расширение линии числа в школьном курсе математики

Основные цели работы: познакомиться с содержани­ем линии числа; выполнить методический анализ содержания; выявить методические аспекты построения теории числа ­в школьном курсе: рассмотреть различные способы введения понятий линии числа, действий и свойств действий.

Вопросы для повторения:

Блок А (вопросы для контроля и самоконтроля содержательного характера)

1. Верно ли утверждение: «Натуральные числа делятся на простые и составные»?

2. Курочка Ряба несет яйца, каждое второе – простое, каждое третье – золотое. Может так быть?

3. Запишите словами: НОД (24, 30) = НОК (2, 3).

4. Почему множество рациональных чисел обозначается буквой Q?

5. Каким дополнительным свойством обладает сравнение в Q по отношению к сравнению в Z (Z – множество целых чисел)?

6. Каким дополнительным свойством обладает сравнение в R по отношению к сравнению в Q (R – множество действительных чисел)?

7. Запишите словами: – 7,8(4).

8. Каждому действительному числу ставится в соответствие пятая цифра после запятой в его десятичной записи. Будет ли это соответствие функцией? Ответ поясните.

9. Запишите в виде бесконечной десятичной дроби сумму 0,(31) и 2,(125).

10. Могут ли одновременно и сумма, и произведение двух иррациональных чисел быть рациональными? Если да, приведите примеры.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3