3.2 Осадочная дифференциация обломочного материала

Транспортировка твёрдых частиц водным потоком осуществляется тремя механизмами, взаимосвязь которых задаёт последовательность фиксации на дне бассейна: перенос в виде дисперсоида, когда участие дна несущественно; сальтация, когда частицы обладают достаточной энергией для отскока от дна; и путём волочения, когда частицы не отрываются от ложа бассейна. Каждый из этих механизмов описывается своим математическим формализмом, но в условиях непрерывности потока, которое выполняется практически всегда, они в целом подчиняются общему закону массопереноса потоком, который выражает система гидродинамических уравнений Сен-Венана [5]:

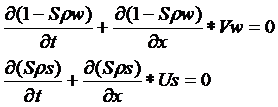
(3.1)

Здесь S - объёмная доля частиц в потоке, ρS - плотность и US - скорость частиц твёрдой фазы, ρW - плотность и VW - скорость воды, x - расстояние, t - время. Для качественной оценки зависимости гидродинамической крупности осадка ω от расстояния до береговой линии Х или глубины бассейна Н, в допущении, что они линейно связаны между собой, т. е. Х = kН, можно получить общий вид приближенного решение системы уравнений Сен-Венана:

ωх = k1 ω0 R0 (exp – qx/V0 ) + k2 ω0 R0 Re{sin[k3 (Х-ct)] – sin[k4 (H-ct)]} (3.2)

Здесь ωх – средняя гидродинамическая крупность осадка, как функция от «Х»;

ω0 - начальная гидродинамическая крупность осадка, R0 - средний начальный радиус частиц, V0 - начальная скорость потока, k1 - k4, q - принимаемые за константы параметры, с – скорость турбулентных пульсаций, Re - число Рейнольдса, по которому потоки разделяются на ламинарные и турбулентные.

Re = u (Vd DS ρd )/μ (3.3)

Здесь Vd, ρd и DS – скорость, плотность и средний диаметр минеральных частиц в дисперсоиде, μ – его вязкость, значение u выбирается таким, чтобы при Re≥1 поток становился турбулентным и в нём появлялись пульсации.

Зависимость (3.2) содержит два слагаемых, причём первое не зависит от времени. Если скорость потока мала, вторым слагаемым можно пренебречь. Тогда крупность осадка будет монотонно снижаться по экспоненциальному закону с увеличением расстояния транспортировки, формируя в результате последовательность нормального литологического ряда от песчаника к глине. При турбулентном потоке на эту зависимость накладывается и периодическая составляющая, в которую будут давать свой вклад время и глубина бассейна. Отсюда следует крайне важный в генетическом плане вывод: если в разрезе фиксируют частое чередование пород разного гранулометрического состава без чётких границ между ними, то это не обязательно означает смену неких условий седиментации и фациальной обстановки. Такая гидродинамическая цикличность всегда будет иметь сугубо локальный характер по времени или месту; а попытки коррелировать даже соседние разрезы по близкому облику пород неизбежно могут привести к грубым и дорогостоящим ошибкам.

Уравнение 3.1, хотя остаётся справедливым для любого массопереноса, пока поток непрерывен, не раскрывает механизмов сальтации и волочения по дну. На качественном уровне первый можно представить как периодические отскоки частиц от дна с вовлечением в поток и движением, которое должно сопровождаться накоплением кинетической энергии. Физически параметры этого процесса описывает число Фруда - Fr, характеризующее соотношение взаимодействий частиц с потоком и дном. Пренебрегая различием плотности частиц и зависящей от температуры вязкостью воды, значение Fr примет вид:

Fr = V2 / fa L (3.4)

где V – скорость потока, т. е. преимущественно воды; fa – сила отскока, в ней участвует упругое взаимодействие с дном и сила Архимеда, зависящие от g; а L - «длина скачка». Раскрывать более подробно содержание этих величин нет смысла, достаточно оценить силу, действующую на частицу в потоке. Можно в грубом приближении допустить, что она пропорциональна силе торможения Стокса - fс для движущейся частицы в неподвижной жидкости, которая равна:

fс = 6π R V μ (3.5)

где: R - радиус частицы, а μ - вязкость. Допустив, что скорость частицы U пропорциональна V, и выразив все принимаемые за константы величины за некий коэффициент С можно представить выражение (3.4) в виде:

Fr = U fс / С R fa L (3.6)

Уравнение (3.6) позволяет достаточно наглядно выявить роль числа Фруда на формирование текстуры осадка. При Fr << 1, когда величина числителя мала, энергии потока недостаточно для сальтации, возникают плоско параллельные слои. При Fr < 1 силы fa и fс становятся соизмеримыми и за счёт сальтации образуются перемещающиеся в направлении потока асимметричные валики, что ведёт к появлению волнистой слоистости. Особое значение имеет случай Fr ≈ 1, когда силы fa и fс взаимно компенсируют друг друга. Очевидно, что равенство Fr = 1 может строго выполняться только при вполне определённых соотношениях значений U и R т. е. для каждого критического радиуса Rк существует критическая скорость Uк при которой сальтация прекращается, но поскольку L ≠ 0 движение частиц продолжается, и возникает так называемый «стреляющий поток». В осадке снова образуются плоско параллельные слои. Соотношение между U к и Rк для этого случая можно получить из (3.6):

Uк = С Rк L (fa / fс) (3.7)

Реализация этих механизмов имеет серьёзные литологические следствия: Во-первых: однонаправленный ламинарный поток может создать в слоевом комплексе резкие литологичекие границы. Соотношение (3.2) их появления не объясняет. При отсутствии сальтации мы всегда имели бы плавные границы. Во-вторых: если однонаправленный ламинарный поток не содержит частиц с размерами, превышающими некоторые критические, то вне независимости от места локализации данного участка бассейна, накопление осадков в нём может отсутствовать без проявлений размыва или выхода на поверхность. Частицы с размерами несколько меньше критических будут перемещаться в так называемом «связанном слое» вдоль поверхности дна и не фиксироваться. Поэтому толщина осадков определённого стратиграфического таксона на его конкретном разрезе, особенно в условиях развития переходных фаций, может быть намного меньше произведения средней расчётной скорости образования осадков на соответствующий интервал геологического времени, за который толща не выходила на дневную поверхность. Примеры таких ситуаций имеют место и на отложениях современного шельфа, так и в более древних разрезах. В-третьих: если в однонаправленном ламинарном потоке происходит плавное снижение скорости, то может возникнуть закономерное наложение слоёв, каждый из которых будет характеризовать индивидуальный, относительно постоянный размер частиц. Реализуемость такого предельно выраженного по интенсивности механизма дифференциации осадков была экспериментально подтверждена. В созданный на километровом желобе поток вносилась смесь нескольких фракций из одинаковых по размеру, но не цвету шариков. В итоге получен слоевой комплекс с почти идеальным разделением слоёв по размеру.

При Fr > 1 уже осевшие частицы могут перемещаться потоком, почти не отрываясь от дна. При этом появляются валы, формирующие диагональную или косую слоистость потокового типа. Прежде всего в движение вовлекается осадок с гребня вала и мобилизованные частицы приобретают способность к перемещению до основания очередного вала. Валы будут двигаться навстречу потоку и становятся симметричными. Присутствовавшие в осадке частицы с размерами меньше критических уносятся потоком за счёт сальтации. Поэтому русловые отложения при средней сортировке обеднены мелкими фракциями.

3.3 Химическая и физико-химическая осадочная дифференциация

Дифференциация веществ при осаждении из истинных водных растворов подчиняется закону химических равновесий: чем меньше растворимость, тем раньше данный минерал выпадет в осадок. На начальной стадии образования эвапоритов появляется или первичный доломит (лагуна Куронг в Австралии), но чаще неупорядоченный кальцит, быстро преходящий в ассоциацию гипса с доломитом при наличии в системе сульфат - аниона по реакции Гейдингера:

2Ca CO3 + Mg SO4 +2H2 O → (Ca, Mg) (CO3 )2 + Ca SO4*2H2 O

Затем выпадают сульфаты щелочных металлов, а заканчивается процесс на кристаллизации сильвина, или галита - во внутри континентальных бассейнах. Катионы железа или марганца могут находиться в растворе лишь в закисной форме, усиливая этим способность к изоморфному замещению в карбонатах. Но в открытых бассейнах значительная их часть присутствует как комплексы с гуминовыми или фульвовыми кислотами, что тормозит окисление. Поэтому при высоких кларковых содержаниях фазы марганца и железа редко бывают первичными осадками. Родохрозит образуется только в локальных впадинах шельфа, а оксиды марганца часто концентрирует гиалоклин, - резкая граница воды с разной солёностью и Eh, периодически возникающая в опресняемых бассейнах. При его разрушении идёт быстрое окисление накопленного Mn2+. Вопрос о первично осадочном синтезе глауконита или шамозита (бертьерина) в значительной мере остаётся открытым. Возможно их прямое образование из коллоидных систем или фрагментов слоёв иных слоистых силикатов [34].

Осадочная дифференциация частиц пелитовой размерности реализуется в значительной мере законами физической химии, а не гидродинамики. По этой причине и эрозия глинистых осадков требует значительно большей скорости потока, чем был при их образовании (эффект Хьюльстрёма). Важную роль в седиментации дисперсных силикатов играет солёность вод, т. е. концентрация раствора электролита, при достижении которой определённых величин будет происходить коагуляция глинистых частиц и их осаждение уже как агрегатов, в отличие от собственно коллоидных растворов, где образовавшийся гель не имеет никакой кристаллической структуры. Глинистая суспензия очень резко отличается от коллоидного раствора и по их термодинамическим параметрам. В соответствии с названными явлениями за внешней границей авандельты выделяют три специфичные зоны седиментации: зона осаждения дисперсных минералов – «глинистая пробка»; зона массовой коагуляции органического вещества и органо - металлических коллоидов – «геохимическая пробка»; зона интенсивного развития организмов - «биологическая пробка». Среди главных глинистых минералов быстрее коагулирует смектит как более дисперсный, за ним следуют смешанослойные фазы смектит-иллит и смектит-хлорит, затем аллотигенные слюды и хлориты. Замыкает этот ряд каолинит. Как следствие, в области интенсивного поступления пресных вод иногда может наблюдаться дифференциация дисперсных осадков по минеральному составу, но объяснять этим явлением результат глобального процесса иллитизации смектита нельзя.

3.4 Роль тектоники, изостазии и уплотнения осадков при формировании структурного плана слоевых комплексов осадочных пород

Само подтверждённое сейсмическими данными явление прогибания ложа бассейна на многие тысячи метров в зонах лавинной седиментации указывает на возможность компенсации веса накопившихся осадков ответной реакцией коры и мантии. Такое явление получило название изостазии и важно оценить его масштабы для осадконакопления в пределах платформ. Рассмотрим очень простую модель: пусть в некий момент времени, когда началось накопление осадков, глубина бассейна была Н1 , а толщина сформированных осадочных пород и континентальной коры, характеристики которых нам здесь не важны, равна d. В результате накопления осадка толщиной h глубина бассейна стала Н, а поверхность мантии при неизменном d прогнулась на величину Dm. Если рассматривать h как сумму твёрдой части осадка с нулевой пористостью Dt и толщиной слоя воды, равной объёму пор Dw то: h = Dt + Dw, Н2 = Н + Dw. Тогда при плотности воды ρw и средней плотности осадков ρt , а плотности мантии ρm условие выполнения изостатического равновесия можно выразить:

ρw Н1 + ρm Dm = ρw Н2 + ρt Dt (3.8)

Приняв как оценочные значения: ρw = 1,03 г/см3, ρt = 2,70 г/см3, ρm = 3,3 г/см3, получаем в численной форме: Dm = 0,735 Dt. Поскольку пористость слабо консолидированных осадков составляет порядка 35% , то Dm ≈ 0,48 h; в ходе погружения средняя пористость терригенных осадков снижается на ≈ 20% и Dm ≈ 0,7 (Н - Н1). Таким образом, вклад от изостазии и уплотнения осадков обеспечивает около ¾ глубин прогибания дна бассейна. Отметим, что во всех случаях, когда параметры в (3.8) удавалось определить вполне корректно, это равенство выполнялось с удивительно высокой точностью. Очевидно, что при реализации изостазии должны меняться и свойства самого вещества мантии. Разогрев и понижение вязкости астеносферы было действительно обнаружено под рядом осадочных бассейнов и проявлялось в погружении границы Мохо на 20 – 40м. Есть указания на возможное участие в таких явлениях и плюмов.

Рассматривая структурный план той или иной территории, мы иногда не учитываем её реальных линейных размеров, применяя термин «тектоническое строение» к перечню поднятий и прогибов любого масштаба. Очевидно, что регионально выраженные структурные формы, такие как своды, валы, мульды или депрессии, рифты и. т.д. связаны своим происхождением с эндогенными, протекающими в коре и мантии процессами, и имеют, в строгом смысле этого термина, тектоническую природу. Но среди них отсутствуют такие, которые способны «проткнуть» литосферную плиту, сформировав перспективное для поисков нефти поднятие с размерами не более нескольких километров. Таким образом, реальный структурный план любого геологического объекта задаёт совокупность многих процессов, в том числе экзогенных, включая изостазию, а так же прочностные и упругие свойства осадочного чехла и фундамента.

3.5 Механизмы формирования породно-слоевых комплексов

Рассмотрим теперь механизм, по которому смена осадков нормального литологического ряда становится последовательностью пластов или слоёв и формирует закономерную, т. е. без вклада гидродинамической цикличности, слоевую ассоциацию, или слоевой комплекс, или секвент, что одно и то же, в геологическом пространстве и времени. На дне бассейна, поверхности только что образованного осадка, V = 0 и первое равенство в (3.1) обращается в нуль. Тогда во втором уравнении величину US можно рассматривать как скорость поступления в бассейн исходного материала и обозначить Uх так как US =φ(х). Плотность обломков, среди которых чаще преобладает кварц и полевой шпат, можно считать постоянной и принять SρS за некую величину Qх, она должна отвечать в любой точке х осадку конкретного гранулометрического состава.

Известно, что на протяжении достаточно продолжительного интервала t между глубиной бассейна, т. е. координатой Z, и временем существует вполне значимая связь. Это позволяет произвести замену переменных и представить для всего осадочного бассейна второе уравнении системы Сен-Венана в виде:

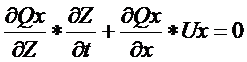(3.4)

Перепишем это выражение через горизонтальную - Ex и вертикальную - Ez компоненты скорости изменения гранулометрического состава осадка (либо фации), а так же относительной глубины бассейна - Uz независимо от того, чем оно вызывается, смещением дна бассейна или уровня его поверхности:

Ez Uz = - Ex Ux (3.5)

или: Ex = - Ez (Uz / Ux) (3.5а)

что является корректным выражением известного закона , который в общем случае можно сформулировать как: «Смещение фаций по горизонтали отвечает их литологическому отображению в вертикальном разрезе с точностью до соотношения скоростей изменения глубины бассейна и поступления в него терригенного материала», это первый геологический закон, имеющий такое же строгое физическое обоснование как закон Стокса.

Выберем точку Ах на дне бассейна, которая расположена на стыке зон накопления осадков типа q и типа r, рис. 3.1. Теперь величина Ux становится конкретным вектором Ūх и его начало может быть совмещено с точкой Ах. В соотношении (3.5) все величины, если они относятся к точке Ах, становятся векторными и приобретают вполне конкретный смысл. Скорость накопления толщины осадка в этой точке есть вектор Ēz, его значение задаёт вектор Ūх со своим углом наклона к горизонту - β, и уголом наклона дна бассейна - α:

[Ēz] = [Ūх] Sin (β – α) (3.6)

а уменьшение глубины при накоплении осадков с учётом их уплотнения на К:

[Ūm] = - [Ēz] Cos (α) •K (3.7)

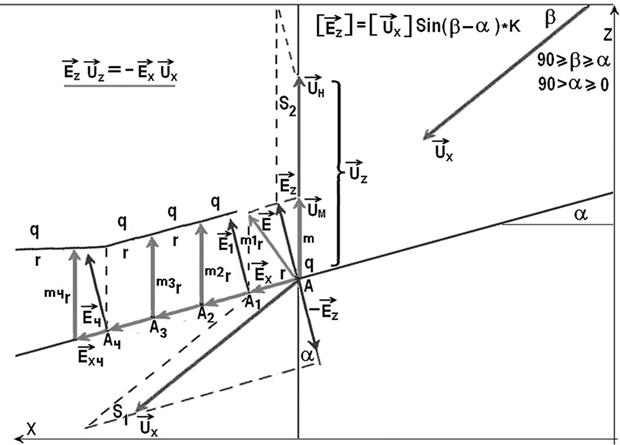
Рис. 3.1 К выводу закона Головкинского и образования последовательности слоёв.

Вектора Ēz и Ēх представляют собой вертикальную и горизонтальную компоненты полного вектора скорости смещения фации Ē и границы между осадками типа q и r. Вектор Ēz не может быть направлен вниз, поэтому в уравнении (3.7) нужно сменить знак. Соотношение (3.5) для векторов требует равенства векторных произведений, и компонента Ēх находится из условия равенства площадей S1=S2, тогда полный вектор Ē определяется правилом параллелограмма.

Чтобы перейти от скоростей к линейной картине процесса седиментации достаточно умножить вектор Ē на некий постоянный интервал времени ∆t, пусть он будет таким, чтобы при (∆t Ēх) точка А переместилась в точку А1. За это время над точкой А1 накопится осадок r толщиной m1r. Если на интервале А – А2 не произойдёт никаких изменений условий седиментации, то за время 2∆t точка А переместится в точку А2 и тот же осадок накопится над точкой А2 с m2r = 2m1r. Аналогично при тех же условиях над точкой А3 сформируется осадок типа r с m3r = 3m1r и. т.д. Появится литологическая граница между r и q слоями, пространственная ориентация которой будет целиком определяться величиной, углом наклона и постоянством вектора Ē. Так, если за время 4∆t условия седиментации изменятся, то другим станет и её наклон, а m4r ≠ 4m1r. Из приведённых построений вытекает первое и крайне важное следствие из закона Головкинского: «В общем случае границы между пластами в слоевом комплексе не могут быть ни горизонтальными, ни изохронными». Это вполне очевидное положение, лежащее в основе любых построений в стратиграфии, к сожалению долго не понималось геологами, и сейчас не всегда понимается.

Рассмотрим теперь закономерности, которые определяют конфигурацию соевой последовательности при периодических изменениях глубины бассейна седиментации, т. е. расстояния между дном и поверхностью, пока независимо от вызывающих их причин. Характер изменения задаёт вектор Ūz, который является суммой векторов ŪH - скоростью изменения уровня моря, и Ūm - скоростью накопления осадка. При отсутствии размыва Ūm > 0 всегда, а ŪH может быть направлен как в ту же сторону ŪH > 0 (дно поднимается), так и в противоположную ŪH < 0. В первом случае смещение фаций произойдёт от берега к морю – обычная регрессия (рис. 3.1). Во втором случае возможны следующие варианты: если ŪH < 0 при [ŪH] > [Ūm], возникнет трансгрессия, море будет наступать на берег, и нужно поменять на + знак в (3.7), чтобы разностный вектор Ūz не был направлен в осадок. Тогда меняется знак и у Ēх, он принимает противоположное направление – к берегу. Возможен и вполне реален вариант, когда при ŪH < 0 возникает примерное равенство [ŪH] ≈ [Ūm], т. е. толщина накапливающихся осадков полностью компенсирует увеличение глубины бассейна, это так называемый режим стабилизации - “top lap” или «перекрывание высокого уровня» при котором смещения границы между фациями не происходит. И, наконец, вариант, когда ŪH < Ūm при ŪH < 0. При высоком уровне бассейна скорость накопления осадков превышает скорость увеличения глубин. Возникает так называемая «регрессия высокого уровня», при которой вектор Ēх снова направлен к морю, но характеризуется малыми значениями модуля. Признание четырёх, а не двух, принципиально разных условий седиментации, является важнейшим отличием теории секвенций от постулатов «классической» литологии.

Изложенные построения позволяют представить динамику формирования геометрического облика двумерного среза геологических тел, т. е. внутренней структуры секвента, при смене этапов осадочного процесса в том же порядке. При регрессии величина Ēх вблизи береговой линии мала и слабо меняется, поскольку мал угол β и, как следствие, модуль вектора Ēz при большом [Ūх]. Наклон пластов, - это наиболее крупнозернистые породы, относительно мал. Затем при увеличении угла β и относительно большом [Ūх] наклон вектора Ē быстро растёт. Наклон слоёв стремится к максимальному в данном секвенте. С удалением от берега величина Ēх снова начинает уменьшаться уже из за уменьшения модуля Ūх и наклон слоёв приближается к наклону дна бассейна. Таким образом, нижняя граница секвента приобретает S - образную форму и может осложняться поверхностями размыва, подводными руслами и барами.

С началом трансгрессии и перехода от тракта спуска– «down lap» на тракт подъёма– «on lap» вектор Ē располагается внутри тупого угла Ēх – Ūz, за счёт этого приобретя почти вертикальную ориентацию. Формируется серия слоёв, близкая к горизонтальной, и перекрывающая с угловым несогласием, которое возрастает с приближением к берегу, подстилающие слои тракта спуска. При этом вблизи береговой линии может возникнуть единое песчаное тело из разных по времени образования слоёв с различными углами наклона. Далее с наступлением режима стабилизации размеры этого слоевого комплекса могут увеличиваться, но по мере смещения в сторону бассейна толщина отдельных слоёв будет уменьшаться и между ними начнут возникать глинистые прослои. Такой путь в обстановках прибрежно-морских фаций задаёт клиноформную структуру многих промысловых объектов, пласта Д1 Ромашкино, например.

Переход к регрессии высокого уровня, сначала относительно плавный, ведёт в дальнейшем к формированию ещё одной, помимо границ секвенции, поверхности угловых несогласий, так называемой “down lap surface”, в нашей терминологии – «поверхности регрессии», которая не содержит фактических размывов. Она обычно уверенно фиксируется на временных разрезах метода ОГТ, хотя граничащими на всём её протяжении становятся различные по своему литологическому облику породы. Такая поверхность не может быть горизонтальной, но она изохронна, так как фиксирует форму дна бассейна во время смены режима стабилизации на «down lap». Перекрывающий комплекс слоёв при этом резко меняет углы наклона, от почти горизонтальных к круто падающим, при плавном переходе к этапу обычной регрессии. Проницаемые породы несогласно налегают на глинистую пачку предыдущей трансгрессии, задавая ещё одну область локализации клиноформ. При завершении этапа формируется верхняя граница секвента. Она тоже имеет S - образную форму, и секвент становится «геологической чечевицей» Головкинского – рис. 3.2.

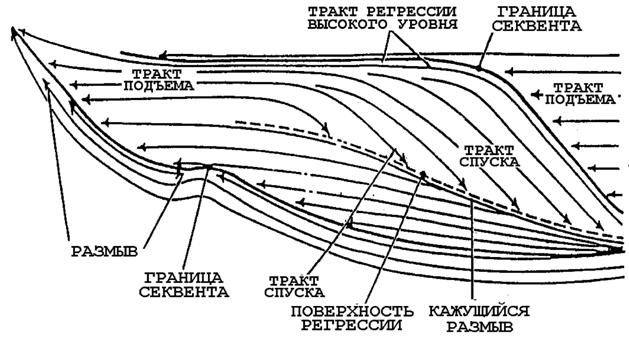
Рис. 3.2. Внутренняя структура секвента (по Ван-Вагонеру, Митчуму, Вэйлу).

4. стадия диагенеза

Под термином «диагенез» в отечественной литературе принято именовать всю совокупность явлений, происходящих в не консолидированном осадке и превращающих этот осадок в осадочную горную породу. Но в англоязычных источниках под термином “Diagenesis” понимают все вторичные изменения пород, скорее всего, по традиции с тех времён, когда любые преобразования осадков связывались только с увеличением температуры и давления. Однако уже при низких РТ параметрах отсутствие равновесия между поступающим в бассейн материалом и меняющимися гидрохимическими характеристиками иловых вод может приводить к серьёзным изменениям не только плотности, но и минерального состава накапливающихся осадков. Мы снова имеем дело с установлением термодинамического равновесия в относительно закрытой системе, которой в данном случае являются образованные в совершенно иных условиях фазы минералов и раствор. Кроме физических, физико-химических и химических явлений важную роль здесь опять играют биогенные процессы, в значительной мере определяющие знак и величину редокс-потенциала для иловых вод. Аэробная микрофлора способна существовать только в верхней зоне слабо уплотнённого осадка, при погружении в его толщу идёт быстрая смена окислительного потенциала на восстановительный, особенно если это сопровождается появлением микробов сульфат-редукторов, переводящих SO4 анион в сероводород. Таким образом, в ходе седиментации область перемены знака Eh движется вверх, синхронно смещая и зону связанных с ней реакций.

Интенсивность и скорость установления равновесия в большой степени будет определяться типом литогенеза. При нивальном литогенезе они слабо проявлены, поскольку в бассейн сносится слабо изменённый аллотигенный, в основном, материал, почти лишенный пелитовой компоненты, за отсутствием развитых кор выветривания. В таких условиях даже при обилии планктона биокосные процессы не могут активно проявиться. При гумидном литогенезе, напротив, гидролиз любой природы в полной мере реализуется ещё в области источников сноса и материал осадков приводится в равновесие со средой до седиментации, отражая всю специфику материнских пород в гораздо большей степени, чем фациальные обстановки бассейна. Процессы диагенеза, поэтому, наиболее контрастно проявляются в условиях аридных ландшафтов, когда с континента сносится уже сильно преобразованный, но ещё не приведённый в состояние равновесия материал, включающий и глинистые минералы. Кроме того, поступающее в осадок органическое вещество не успевает здесь сильно окислиться, как в гумидных обстановках, чем обеспечивается максимальная интенсивность явлений биологической природы. Как следствие, минеральный состав осадочных толщ аридного литогенеза должен, прежде всего, отражать гидрохимию бассейна, тем более, что при этом она часто бывает аномальной.

Многие процессы диагенеза являются тривиальными, они включаю в себя снижение пористости, а так же увеличение концентрации иловых вод, в том числе и за счёт элементов исходно низкой концентрации. Поэтому возможно образование путём прямого синтеза минералов, для которых концентрация их компонент в открытом бассейне никогда не достигает предела насыщения. К ним относятся плохо окристаллизованный фосфат, гидроксил - апатит и фазы закисного железа и марганца. Рост конкреций сидерита обычно приурочен ко времени минимального поступления обломочного материала, т. е. к режиму стабилизации осадочного процесса, что позволяет использовать их для целей корреляции разрезов, в отличие от других аутигенных минералов, например пирита. Железо-марганцовые конкреции, а так же железистые силикаты типа бертьерина и глаукониты так же возникают преимущественно в диагенезе.

4.1 Сорбция и катионный обмен при диагенезе осадков

Большинству явлений кристаллогенезиса на этой стадии предшествуют явления ионного обмена и сорбции, под которыми понимают аккумуляцию вещества или замену одного вещества на другое на границе раздела фаз. Адсорбция отличается от процесса осаждения вещества из раствора тем, что в последнем случае формируется трехмерная кристаллическая структура на твердой поверхности. Поэтому природу таких явлений следует рассмотреть более подробно. Поверхность раздела между минеральными частицами и раствором - это не просто плоскость, а трехмерная специфическая область, непохожая по своим составу и свойствам ни на минеральную частицу, ни на окружающий раствор. Поскольку поверхность частиц всегда имеет заряд, на поверхности и вблизи неё в этой области раствор концентрируют катионы металлов и лиганды, принимающие участие в нейтрализации заряда. В основе теории двойного электрического слоя, описывающего совокупность таких явлений, используются концепции коллоидной химии. При взаимодействии функциональных групп на поверхностях твердых частиц с компонентами раствора формируются внешнесферные и внутрисферные комплексы. Для первых между поверхностью минерала и поглощаемым катионом находятся молекулы растворителя, в частности воды, которые препятствуют развитию ковалентных связей. Поэтому ион удерживается на поверхности относительно слабыми электростатическими силами. Такой тип взаимодействия определяют как неспецифическую адсорбцию, к нему же относится значительная часть реакций ионного обмена. При образовании внутрисферных комплексов между центральным катионом и лигандом нет молекул растворителя (воды), что определяет возможность развития прочных ковалентных связей. Образование поверхностных внутрисферных комплексов определяется как специфическая адсорбция. В обоих случаях поверхность минерала имеет заряд, вызывающий притяжение ионов противоположного знака, на границе раздела твердой фазы и раствора возникает электрический потенциал, и формируется двойной элек-трический слой ДЭС (английская аббревиатура EDL), который состоит из слоя потенциал-определяющих ионов и слоя ионов, компенсирующих заряд.

В наиболее используемой модели Гюи-Чапмена граница раздела между твердой частицей и раствором представляет собой плоскую поверхность с равномерным распределением отрицательного или положительного заряда, но противоионы подвергаются воздействию противоположно направленных сил электростатического притяжения, и диффузии. В результате равновесия между этими силами на границе слоя из потенциал-определяющих ионов формируется диффузный слой, в котором могут присутствовать не только ионы противоположного знака, но и того же знака, что и у потенциал-определяющих ионов. В последнем случае концентрация ионов в диффузном слое значительно ниже, чем в окружающем растворе за счет сил отталкивания между ионами одного знака. Концентрация противоионов в диффузном слое постепенно падает при продвижении от поверхности частицы в раствор. При этом изменение электрического потенциала в зависимости от расстояния х от поверхности описывается экспоненциальной функцией вида [16]:

Ψ(x) = Ψ(d) = Ψ(0) exp(-kx) (4.1)

где Ψ(х) = Ψ(d) - потенциал на расстоянии х по толщине диффузного слоя, κ - параметр, равный расстоянию от плоскости противоионов до той плоскости, которая проходит через центр зарядов в диффузном слое, либо его толщина. Распределение концентрации катионов и анионов диффузного слоя в модели Гюи-Чапмена подчиняется уравнению Больцмана:

(4.2)

где cx - концентрация на расстоянии x от поверхности, cB - концентрация в окружающем растворе.

По модели Штерна на заряженной поверхности потенциал-определяющих ионов находится плотный слой противоионов с постоянной концентрацией, (модель Гельмгольца). Далее следует диффузный слой модели Гюи-Чапмена. Уравнения, описывающие изменение концентраций катионов и анионов в пределах плотноупакованного и диффузного слоев, отвечают соответственно моделям Гюи-Чапмена и Гельмгольца, в которой зависимость между зарядом и потенциалом поверхности описывается простым соотношением: σ = С Ψ [16].

В соответствии с принципами термодинамики, адсорбция - спонтанный процесс, направленный на снижение свободной энергии поверхности раздела и на выравнивание химических потенциалов веществ в объеме системы и на границе раздела фаз. Этот процесс может быть описан уравнением Гиббса:

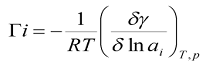(4.3)

здесь Гi - концентрация i-ого компонента на поверхности раздела фаз (моль/м2), γ - поверхностное натяжение на поверхности раздела (Дж/м2), аi - активность i-ого компонента в жидкой фазе. Из уравнения (4.3) следует, что вещества, снижающие поверхностное натяжение 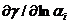< 0, будут аккумулироваться.

Катионный обмен в строгом смысле слова – это обратимый процесс, при котором обмен катионов должен осуществляться в соответствии с законами стехиометрии и эквивалентно. Вводится понятие об эквивалентном числе катиона – количестве молей катиона, которое замещает один моль протонов, поскольку один моль протонов соответствует одному молю заряда. Правило эквивалентности соблюдается при адсорбции далеко не всегда. В реакциях катионного обмена могут участвовать катионы внешнесферных комплексов и катионы, находящиеся в диффузном слое, в то время как процесс адсорбции включает в себя реакции образования не только внешнесферных, но и внутри-сферных комплексов. Особый интерес для нас в процессах ионного обмена играет смектит и смешанослойные фазы с межслоевыми промежутками типа смектита или вермикулита, в которых гидратированные катионы локализуют дитригональные петли базальных кислородов в тетраэдрических сетках.

Обменные катионы удерживаются на указанных выше позициях силами электростатического притяжения, величину которого задаёт закон Кулона:

(4.3)

где F - сила кулоновского взаимодействия частиц, q+ и q- величины зарядов противоположно заряженных ионов, ε - диэлектрическая постоянная среды, а r - расстояние между зарядами.

В соответствии с законом Кулона сила связи катиона с твердой фазой должна возрастать с увеличением валентности катиона, а с увеличением ионного радиуса, при равной валентности, снижаться, т. е. зависеть от ионного потенциала Гольдшмидта, равного r/z, где r– радиус иона, а z его валентность. Это значит, что на одном и том же типе сорбционных центров одни катионы по сравнению с другими должны сильнее поглощаться, или удерживаться с большей энергией связи. Для одновалентных и двухвалентных катионов ряды по возрастанию радиуса иона и, соответственно, росту способности к преиму-щественному поглощению или замещению других катионов в межслоевым пространстве имеют вид (в скобках приведён размер ионного радиуса в Ǻ):

Li+(0,59) < Nа+(1,02) < К+(1,34) < Rb+(1,52) < Сs+ (1,67), рисунок 4.1, и

Mg2+(0,72) < Ca2+(1,04) < Sr2+(1,18) < Ba2+(1,

Все эти катионы относятся к группе I диаграммы Гольдшмидта, для которой величины ионного потенциала достаточно только для поляризации молекул воды в гидратно-ионном комплексе, на поверхности которого локализуются группы (ОН), давая раствору щелочную рН (щелочные и щёлочноземельные катионы). Они формируют относительно легко растворимые водой минералы. В межслоевом пространстве смектита двухвалентные катионы координируют две сетки молекул Н2О, а одновалентные Li+ и Nа+ - одну (см. Приложение). Ввиду низкого ионного потенциала К+, Rb+, Сs+ не образуют гидратно-ионных комплексов, что облегчает их сорбцию минералами и не даёт возможность формировать непрерывные сетки Н2О в межслоевом пространстве смектитов. Это так называемые «антистоксовские» катионы, их движение в растворе не подчиняется закону Стокса. Как следствие, при химической близости Nа+ и К+ они являются геохимическими антиподами: К+ «не доходит» до бассейнов, а Nа+ преимущественно накапливается уже в океанах и эвапоритах.

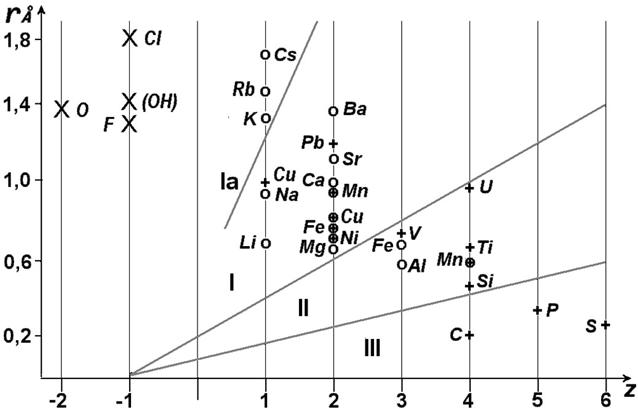
Рис. 4.1 Диаграмма Гольдшмидта, иллюстрирующая различия поведения ионов в растворе. «Твёрдые», «Мягкие» и «Промежуточные» кислоты, по Льюису-Пирсону [51] обозначены как O, + и Å соответственно, «Твёрдые» основания – как X.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4