Предмет и метод статистики, связь с другими науками (стр. 2 )

Б) Переменный вес – вес текущего периода. С переменными весами рассчитываются индексы цен (индекс Пааше, где q1 – переменный вес).

4) В зависимости от формы построения

В зависимости от формы построения различаются индексы агрегатные и средние.

А) Агрегатный индекс – сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина – признак, изменение которого изучается), а другая остается неизменной в числителе и знаменателе (вес индекса). Агрегатные индексы – основная форма общих индексов.

Пример: Ip = 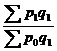- агрегатный индекс цен с весами текущего периода (формула Пааше).

Б) Средние индексы – производные, они получаются в результате преобразования агрегатных индексов, а следовательно, тождественны им. Средний индекс вычисляется как средняя величина из индивидуальных индексов. Средние индексы делятся на арифметические и гармонические.

a) Средний арифметический индекс тождествен агрегатному индексу, только если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса.

Например, Iq = 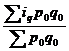- средний арифметический индекс физического объема продукции, где весом является стоимость продукции базисного периода, также как и в формуле Iq = 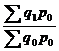. Так как iqq0 = q1, то обе формулы могут быть преобразованы друг в друга.

b) Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса.

Например, Ip = 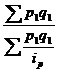- средний гармонический индекс цен, где весом является стоимость продукции текущего периода, также как и в формуле Ip = .

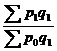Так как = p0, то обе формулы могут быть преобразованы друг в друга.

5) по характеру объекта исследования

По характеру объекта исследования общие индексы подразделяются на индексы количественных и качественных показателей. В основе такого деления лежит вид индексируемой величины. К первой группе, например, относятся индексы объема продаж долларов США на ММВБ, а ко второй – индекс курса немецкой марки.

6) по объекту исследования

по объекту исследования индексы бывают: производительности труда, себестоимости, физического объема продукции, стоимости продукции и т. д.

7) по составу явления

По составу явления можно выделить две группы индексов: постоянного (фиксированного) состава и переменного состава.

А) Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Индекс переменного состава отражает изменение не только индексируемой величины, но и структуры совокупности (весов).

Например: Iпс = = 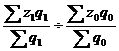- индекс переменного состава себестоимости продукции.

Б) Индекс постоянного состава – индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Индекс фиксируемого состава определяется как агрегатный индекс.

Например: Iфс = 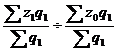= 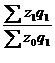- индекс фиксированного состава себестоимости продукции.

8) по периоду исчисления

По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные.

24. Индивидуальные индексы стоимости (товарооборота), цен и физического объема.

Индивидуальные индексы получают в результате сравнения однотоварных явлений. Например, индекс цен на растительное масло определяется как отношение цены на этот товар в текущем периоде к цене базисного периода.

В зависимости от экономического значения индивидуальные индексы бывают физического объема продукции, цен, товарооборота и т. д.

1) Индивидуальный индекс физического объема продукции

Индивидуальный индекс физического объема продукции iq рассчитывается по формуле: iq = , где q1 – физический объем данного товара в текущем периоде, а q0 – физический объем данного товара в базисном периоде.

Этот индекс показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным, или сколько процентов составляет рост (снижение) выпуска товара. Если из значения индекса, выраженного в процентах, вычесть 100%, то полученная величина покажет, на сколько процентов возрос (уменьшился) выпуск продукции.

2) Индивидуальный индекс цен

Индивидуальный индекс цен ip рассчитывается по формуле ip = , где p1 – цена на данный товар в текущем периоде, а p0 – цена на данный товар в базисном периоде. Таким образом, этот индекс характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным.

3) Индивидуальный индекс стоимости продукции

Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на ее цену (p).

Индивидуальный индекс стоимости продукции ipq рассчитывается по формуле

ipq = , где p1q1 – стоимость данного товара в текущем периоде, а p0q0 – стоимость данного товара в базисном периоде.

Этот индекс отражает, во сколько раз изменилась стоимость какого-либо товара в текущем периоде по сравнению с базисным или сколько процентов составляет рост (снижение) стоимости товара.

При этом: ip iq = ipq

Пример № 1

Имеются следующие данные об объеме продаж картофеля на муниципальном рынке в одном из городов страны:

Вычислить индивидуальные индексы цены, физического объема и стоимости картофеля.

Решение:

а) Индивидуальный индекс физ. объема.

iq = = = 1,25 (или 125%)

Мы получили, что физ. объем проданного картофеля в текущем периоде по сравнению с базисным возрос на 25% (125%-100%), или на 5000 кг, и составил 125% от уровня продаж базисного периода.

б) Индивидуальный индекс цен.

ip = = = 1,5 (или 150%)

Мы получили, что уровень цен на картофель в текущем периоде по сравнению с базисным возрос на 50% (150%-100%), или на 10 руб. за кг., и составил 150% от уровня цен базисного периода.

в) Индивидуальный индекс товарооборота.

ipq = = = 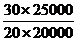= 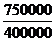1,875 (или 187,5%)

Мы получили, что товарооборот картофеля в текущем периоде по сравнению с базисным возрос на 87,5% (187,5%-100%), или на 350000 руб. (750000 – 400000), и составил 187,5% от товарооборота базисного периода. Рост товарооборота картофеля в текущем периоде по сравнению с базисным произошел как за счет роста цен, так и за счет роста физ. объема продаж.

Пример № 2

Определить индивидуальные индексы цены, физ. объема и стоимости мясных продуктов, если известно следующее:

Решение:

а) Индивидуальный индекс цены.

ip = = =0,909 (или 90,9%)

Мы получили, что уровень цен на мясные продукты в текущем периоде по сравнению с базисным уменьшился на 9,1% (90,1%-100%), или на 0,2 долл. за ед., и составил 90,9% от уровня цен базисного периода.

б) Индивидуальный индекс товарооборота.

ipq = == 1,24 (или 124%)

Мы получили, что товарооборот мясных продуктов в текущем периоде по сравнению с базисным возрос на 24% (124%-100%), или на 2400 долл.(12400 – 10000), и составил 124% от товарооборота базисного периода. Очевидно, что рост товарооборота мясных продуктов в текущем периоде по сравнению с базисным произошел из-за роста физ. объема продаж.

в) Индивидуальный индекс физ. объема

iq = === =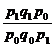= 1,364 (или 136,4%)

Мы получили, что физ. объем проданных мясных продуктов в текущем периоде по сравнению с базисным вырос на 36,4% (136,4% - 100%), или на 1654 кг (12400/2,0 – 10000/2,2) и составил 136,4% от уровня продаж базисного периода.

25. Построение индексов в агрегатной форме. Индексируемая величина и статистический вес.

Агрегатный индекс – сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Особенность этой формы индекса состоит в том, что в агрегатной форме непосредственно сравниваются две суммы одноименных показателей. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной в числителе и знаменателе (вес индекса). Агрегатные индексы – основная форма общих индексов.

Индексируемая величина – признак, изменение которого изучается (цена товаров, курс акций и т. д.)

Вес индекса – величина постоянная, одинаковая в числителе и знаменателе, служит для соизмерения индексируемых величин.

Методика построения агрегатного индекса предусматривает ответ на три вопроса:

А) какая величина будет индексируемой;

Б) по какому составу разнородных элементов явления необходимо исчислить индекс;

В) что будет служить весом при расчете индекса.

При этом, если строится индекс количественного показателя, то веса берутся за базисный период; при построении индекса качественного показателя используются веса отчетного периода.

1) Агрегатный индекс стоимости продукции

Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на ее цену (p).

Индекс стоимости продукции, или товарооборота (Ipq) представляет собой отношение стоимости продукции текущего периода (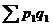) к стоимости продукции в базисном периоде () и определяется по формуле: Ipq =.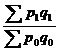

Такой индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции. Если из значения индекса стоимости вычесть 100% (Ipq – 100%), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. Разность числителя и знаменателя (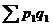-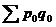) показывает, на сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным.

2) Агрегатный индекс физического объема продукции

Индекс физического объема продукции – это индекс количественного показателя. Здесь индексируемая величина – количество продукции в натуральном выражении, а вес – цена. Только умножив несоизмеримые между собой количества разнородной продукции на их цены, можно перейти к стоимостям продукции, которые будут уже величинами соизмеримыми. Так как индекс физического объема – индекс количественного показателя, то весами будут цены базисного периода. Тогда формула индекса примет следующий вид:

Iq = 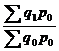, где в числителе дроби – условная стоимость произведенных в текущем периоде товаров в ценах базисного периода, а в знаменателе – фактическая стоимость товаров, произведенных в базисном периоде.

Данный индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объема ее производства или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения физического объема ее производства. Если из значения этого индекса вычесть 100% (Iq – 100%), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным из-за роста (снижения) объема ее производства. Разность числителя и знаменателя (- ) показывает, на сколько рублей изменилась стоимость продукции в результате роста (уменьшения) ее объема.

3) Агрегатный индекс цен

Индекс цен является наиболее широко распространенным показателем инфляции.

Индекс цен – индекс качественного показателя. Индексируемая величина – цена товара, вес – количество произведенных товаров. Умножив цену товара на его количество, получаем величину, которую можно суммировать и которая представляет собой показатель, соизмеримый с другими подобными ему величинами. Так как индекс цен – индекс качественного показателя, то весом будет количество произведенной продукции текущего периода. Тогда индекс цен определяется по следующей формуле: Ip=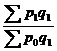, где в числителе дроби – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров в ценах базисного периода.

Индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения цен. Если из значения данного индекса вычесть 100% (Ip - 100%), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции из-за изменения цен, а разность числителя и знаменателя (-) – на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен.

При этом: Ip Iq = Ipq

Пример № 1

Определить общие индексы цен, товарооборота и физического объема, если известно следующее:

Решение:

А) Мясные продукты:

= => q1== = 6200 ед.;

= => q0== =4545 ед.

Б) Молочные продукты:

= => q1== = 15333 ед.;

= => q0== = 16000 ед.

1) Индекс цен:

Ip=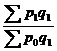 = = =1,014 (или 101,4%).

Мы получили, что общий уровень цен по данным продуктам возрос на 1,4% (101,4%-100%), или в 1,014 раз, и составил 101,4% от прежнего. Перерасход потребителя составил 293,3 (21599,8-21306,5).

2) Индекс физического объема:

Iq = 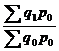= = 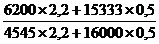= 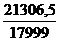1,184 (или 118,4%).

Мы получили, что общий уровень физ. объема возрос на 18,4% (118,4% - 100%), или в 1,184 раз, и составил 118,4% от прежнего уровня.

3) Индекс товарооборота:

Ipq =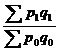= = = 1,2 (или 120%).

Мы получили, что общий уровень товарооборота возрос на 20% (120%-100%), или в 1,2 раз, и составил 120% от прежнего уровня. Рост этого показателя произошел в основном за счет роста объема потребления. Потребитель стал в общем потреблять продукции на 3600 долл. (21600 – 18000) больше.

Используя взаимосвязь индексов, проверим правильность вычислений:

Ip Iq = Ipq=1,0141,184=1,2.

Пример № 2

Что произошло с физическим объемом импорта страны А, если общая стоимость всех закупок возросла в отчетном периоде по сравнению с базисным на 12%, а индекс цен по импорту составил 96%?

Дано:

Ipq = 112%

Ip= 96%

Найти Iq

Решение:

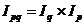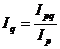=> ==1,167 (или 116,7%).

Ответ: Физический объем импорта страны А возрос на 16, 7% (116,7% - 100%), или в 1,167 раз, и составил 116,7% от прежнего уровня.

26. Средние индексы, тождественные агрегатным.

Кроме агрегатных, индексов в статистике применяются и средневзвешенные. Их рассчитывают, если имеющейся информации недостаточно, чтобы рассчитать общий агрегатный индекс. Например, если нет данных о ценах, но есть – о стоимости продукции в текущем периоде и об индивидуальных индексах цен по каждому товару, то общий индекс цен как агрегатный определить нельзя, но можно вычислить его как средний из индивидуальных. Если же не известны количества произведенных отдельных видов продукции, но известны индивидуальные индексы и стоимость продукции базисного периода, то можно определить общий индекс физического объема как средневзвешенную величину.

Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. Средний индекс производный, он получается в результате преобразования агрегатного, а следовательно тождествен ему.

При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.

Средний арифметический индекс тождествен агрегатному, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса.

Средний арифметический индекс физического объема вычисляется по формуле: 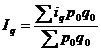. Весами в формуле является стоимость продукции базисного периода. Так как 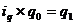, то формула этого индекса легко преобразуется в формулу: .

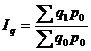Средние арифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей. Индексы качественных показателей обычно определяются по формуле средней гармонической взвешенной величины.

Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса. Например, индекс цен можно вычислить по формуле: 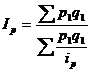, где весами является стоимость продукции текущего периода. Так как 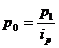, то формула может быть легко преобразована в формулу .

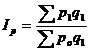Средние индексы также широко применяются для анализа рынка ценных бумаг. Наиболее известным является индекс Доу-Джонса, который определяется как средний арифметический индекс значений курсов акций, котирующихся на Нью-йоркской фондовой бирже.

Пример №1

По нижеследующим данным определить индекс физического объема продукции:

Решение:

1) Индивидуальные индексы объема:

Туфли женские: ;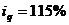

Туфли мужские:;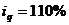

Туфли детские:.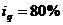

2) Средний арифметический индекс физического объема:

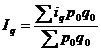===1,,7%).

В среднем физический объем продукции в июне увеличился по сравнению с маем на 7,7% и составил 107,7% от уровня мая.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4