Опять же, можно использовать наивный подход сам по себе, или же использовать его как основу для сравнения и оценки других, более совершенных и сложных методов.
Использование сезонных показателей. Сезонные показатели используются в прогнозировании двумя различными способами. Один способ – исключение сезонности из данных; другой – включение сезонности в прогноз.
Удаляя из данных компонент сезонности, мы получаем более ясную картину несезонных компонентов (например, тенденций). Освобождение данных от сезонности может быть выполнено делением каждой точки данных на соответствующий ей сезонный показатель (например, разделив показатель спроса в ноябре на ноябрьский показатель сезонности, спрос декабря на декабрьский показатель, и т. д.).
Включение сезонности в прогноз целесообразно, когда спрос показывает как тенденцию (или среднее значение), так и сезонные компоненты. Включение сезонности может быть выполнено следующим образом:
1. Получить оценки тенденции для соответствующих периодов, используя уравнение тенденции.
2. Добавить сезонность к оценкам тенденции, умножая (если принята мультипликативная модель) эти оценки тенденции на соответствующий сезонный показатель (например, умножить оценку тенденции ноября на ноябрьский сезонный показатель, оценку тенденции декабря – на декабрьский сезонный показатель, и т. д.).
Это показано в примере 4.
ПРИМЕР 4
Изготовитель мебели хочет предсказать поквартальный спрос на определенную модель двухместного кресла для периодов 15 и 16, которые являются вторым и третьим кварталами текущего года. Ряд включает тенденцию и сезонность. Тенденция спроса прогнозируется, используя уравнение У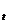
= 124 + 7,5t. Показатели кварталов - Q = 1,20, Q = 1,10, Q3 = 0,75 и Q4 = 0,95. Используйте данную информацию, чтобы предсказать спрос для периодов 15 и 16.
Решение:
Значения тенденции для t=15 и t=16 таковы:
У15 = 124 + 7,5 (15) = 236,5
У16 = 124 + 7,5 (16) = 244,0
Умножив значения тенденции на показатель соответствующего квартала, получим прогноз, который включает и тенденцию, и сезонность. При условии, что t = 15 - это второй квартал и t = 16 - это третий квартал, прогнозы будут следующими:
Период 15: 236,5 (1,10) = 260,15 Период 16: 244,0 (0,75) = 183,00
Вычисление сезонных показателей. Обычный метод для представления тенденции во временном ряде включает использование центрированного скользящего среднего значения.
Вычисления и возникающие в результате значения – такие же как для прогноза скользящего среднего значения. Однако значения не проецируются как в прогнозе; вместо этого они помещаются в середину периодов, которые были использованы для вычисления скользящего среднего значения. Смысл состоит в том, что среднее значение является наиболее представительной точкой в ряде. Например, примем следующие данные временного ряда:
Период | Спрос |
1 | 40 |
2 | 46 |
3 | 42 |
Среднее значение за три периода составило 42,67. Как центрированное среднее значение, оно помещено в период 2; среднее значение наиболее представительно для ряда в этой точке.
Отношение спроса в периоде 2 к этому центрированному среднему значению в периоде 2 – это оценка сезонного показателя в этой точке. Так как отношение 46:42,67 = 1,08, то ряд в данной точке на 8% превышает среднее значение. Для получения приемлемой оценки сезонности для любого значения «сезона» (например, посещаемость театра по пятницам), обычно бывает необходимо вычислить сезонные отношения для ряда сезонов, а затем определить их среднее значение.
Число периодов, необходимых для вычисления центрированного скользящего среднего значения, равно числу точек данных в сезоне. Следовательно, для ежемесячных данных необходимо скользящее среднее значение за 12 периодов. Когда число периодов является четным, необходим один дополнительный шаг, потому что середина четного «набора» попадает между двумя периодами. На этом дополнительном этапе требуется взять центрированное скользящее среднее значения за два периода четного центрированного скользящего среднего значения, что дает средние значения, которые «выстраиваются в линию» по точкам данных и, следовательно, позволяют определить сезонные коэффициенты
Методы для циклических изменений
Циклы – это восходящие и нисходящие движения, подобные сезонным изменениям, но только более продолжительные – от двух до шести лет между пиками. Когда цикл присутствует в данных временного ряда, то из-за их частой нерегулярности бывает трудно или вообще невозможно выявить его в прошлых данных, – потому что трудно определить поворотные моменты. Короткое скользящее среднее значение или наивный подход имеют здесь определенную ценность, хотя оба они дают прогнозы, которые отстают от циклических движений на один или несколько периодов.
Самый распространенный подход заключается в поиске другой переменной, которая предопределяет интересующую нас переменную. Например, число начинающихся строительных работ (т. е. выдача разрешения на строительство здания) в данном месяце часто является индикатором будущего спроса, который может возникнуть несколько месяцев спустя, на изделия и услуги, непосредственно связанные с завершением строительства новых домов (например, обустройство территории; продажа умывальников и сушилок, настилка ковровых покрытий, продажа мебели; новый спрос на магазины, транспортные системы, школы). Таким образом, если организация способна установить высокую корреляцию с такой ведущей переменной (т. е. изменения «ведущей» переменной предшествуют изменениям в переменной, представляющей интерес), – то это даст возможность разработать уравнение, которое описывает связь между переменными, и затем прогноз. Важно, что постоянная связь существует между двумя переменными. Более того, чем выше корреляция, тем больше вероятность, что прогноз окажется точным.
3.4. Ассоциативные методы прогнозирования
Ассоциативные методы основаны на определении взаимосвязанных переменных, которые можно использовать для предсказания значений интересующих нас переменных. Например, продажа говядины может быть связана с ценой за кг говядины, а также с ценой различных заменителей говядины, например куриного мяса, свинины и баранины; цены на недвижимость обычно связаны с расположением собственности; урожайность связана с плодородием почвы, объемом и своевременностью поливки и внесения удобрений.
Основа ассоциативных методов – разработка уравнения, которое суммирует эффекты переменных предсказания.
Первичный метод анализа называется регрессией.
Простая линейная регрессия
Самая простая и наиболее распространенная форма регрессии представляет собой линейную связь между двумя переменными.
Цель линейной регрессии – получить уравнение прямой линии, которая дает минимальную сумму квадратов вертикальных отклонений точек данных от линии. Линия наименьших квадратов отклонений описывается уравнением:
У
= а + bx (9),
где У - предсказанная (зависимая) переменная;
x - переменная-предсказатель (независимая);
b - наклон линии;
а - значение У при x = 0 (т. е высота линии на пересечении с осью У).
Обратите внимание: обычно значения предсказанной переменной показывают на оси У, а значения переменной-предсказателя – на оси X.
Коэффициенты прямой а и b вычисляются по следующим двум уравнениям:
b=
(10),
a=
(11),
где n – число парных наблюдений.
Тщательное определение и анализ индикаторов может дать представление о возможном будущем спросе. Эти данные публикуются и можно выбрать то, что необходимо:
· изменение наличных и заказанных материальных запасов;
· процентная ставка для коммерческих ссуд;
· объем производства;
· индекс потребительских цен;
· индекс оптовых цен;
· цены рынка акций;
· другие потенциальные индикаторы – показатели миграции населения, местный политический климат, действия других компаний (например, открытие торгового центра может в результате увеличить объемы продаж близлежащих торговых точек). Чтобы то или иное событие могло служить индикатором, необходимы три условия:
1. Связь между движением индикатора и движением переменной должна иметь логическое объяснение.
2. Движение индикатора должно настолько предшествовать движению зависимой переменной, чтобы прогноз не устарел прежде, чем его используют.
3. Между двумя переменными должна существовать высокая степень корреляции.
Корреляция измеряет степень и направление связи между двумя переменными. Значение корреляции может находиться в диапазоне от -1,00 до +1,00. Корреляция +1,00 показывает, что изменение одной переменной всегда соответствует изменению другой; корреляция -1,00 показывает, что увеличение одной переменной соответствует уменьшению другой; а корреляция, близкая к нулю, указывает на малую линейную связь между двумя переменными. Корреляцию между двумя переменными можно вычислить с использованием следующего уравнения:
R= (12)
Комментарии по использованию линейного регрессионного анализа
Использование простого регрессионного анализа подразумевает, что удовлетворяются некоторые условия. Основные из них:
1. Колебания около прямой носят случайный характер. Если они случайны, то никакие структуры типа циклов или тенденций не должны проявляться на графике данных.
Отклонения от прямой должны быть нормально распределенными. Концентрация значений близко к прямой с небольшими отклонениями будет свидетельствовать о нормальности распределения.
2. Предсказания делаются только для определенного диапазона наблюдаемых значений.
Если данные условия удовлетворяются, то регрессионный анализ может стать очень эффективным инструментом прогнозирования. Особенно полезными являются доверительные интервалы для предсказанных значений. Для получения оптимальных результатов соблюдайте следующее:
1. Всегда отображайте данные графически, чтобы убедиться в наличии линейной связи.
2. Данные могут зависеть от времени. Проверьте это построением графика зависимой переменной как функции времени; если проявляется закономерность,
то используйте анализ временного ряда вместо регрессионного, или используйте время в качестве независимой переменной множественного регрессионного анализа.
3. Малая корреляция может означать значимость других переменных.
Кроме того, учтите некоторые слабые стороны регрессии:
1. Простая линейная регрессия применяется только к линейным связям с одной независимой переменной.
2. Для установления связи необходимо значительное количество данных, - на практике это 20 или более наблюдений.
3. Все наблюдения имеют одинаковый коэффициент значимости.
IV. Точность и проверка прогнозов
Точность и проверка прогнозов – жизненно важный аспект прогнозирования. Сложная природа большинства реальных переменных делает почти невозможным правильное предсказание их будущих значений на регулярной основе. Следовательно, необходимо включить в прогноз показатель возможного отклонения прогноза от действительного значения переменной. Это позволит лучше представить о степени точности прогноза.
Кроме того, некоторые методы обеспечивают большую точность в данной ситуации, чем другие, – поэтому пользователю необходимо иметь некоторый эталон точности, чтобы использовать его как основу при выборе метода прогнозирования.
Наконец, в некоторых случаях требуется использование нескольких прогнозов (например, недельные доходы), в то время как для других достаточно одноразового прогноза, который будет использован для разового решения (например, определение размера электростанции). Когда делаются периодические прогнозы, то важно контролировать ошибки прогноза, определяя, находятся ли эти ошибки в допустимых пределах. Если нет, то необходимо предпринимать корректирующие действия.
Ошибка прогноза – это разница между фактическим и предсказанным значением.
Следовательно, Ошибка = Фактическое значение –Прогноз:
e =A +F (13).
Значение ошибки бывает положительным, когда прогноз занижен, отрицательным – когда прогноз завышен. Например, если фактический спрос в течение недели – 100 единиц, а прогнозируемый спрос был 90 единиц, – то прогноз был слишком низок; ошибка: 100-90= +10.
Ошибки прогноза влияют на решения двумя различными способами. Один из них заключается в выборе между различными вариантами прогноза, а другой – в оценке успеха или неудачи примененного метода прогнозирования.
4.1. Вычисление точности прогноза
Два аспекта точности прогноза имеют потенциальную значимость при выборе альтернативных вариантов прогнозов. Первый – историческая ошибка выполнения прогноза, а другой – способность прогноза реагировать на изменения.
Для вычисления ошибок прогноза обычно используют два показателя – среднее абсолютное отклонение (mean absolute deviation – MAD) и среднее квадрата ошибки (mean squared error – MSE).
Для вычисления MAD и MSE используются следующие формулы:
MAD= (14),
MSE= (15).
С вычислительной точки зрения, различие между этими двумя показателями заключается в том, что MAD оценивает все ошибки одинаково, a MSE определяет значимость ошибок согласно значениям их квадрата.
Один из способов использования этих показателей – сравнение альтернативных методов прогнозирования. Например, используя MAD или MSE, менеджер может сравнить результаты экспоненциального сглаживания со значениями 0,1, 0,2 и 0,3 и выбрать тот из них, который дает самое низкое значение MAD или MSE.
В некоторых случаях, ошибочность прогноза вторична по отношению к его способности реагировать на изменения в структуре данных. В этом случае предстоит выбор между прогнозом, который медленно реагирует на изменения, – и прогнозом, который реагирует на несуществующие, т. е. случайные, изменения.
В целом, менеджер должен решить, что для него более важно – точность или гибкость прогноза, и использовать ли ему MAD или MSE для измерения точности прогноза.
4.2. Контроль прогноза
Для того чтобы прогноз работал должным образом, ошибки прогноза необходимо контролировать,. Это осуществляется путем сравнения ошибок прогноза с заранее определенным значениями, или границами действия, как показано на рисунке. Ошибки, значение которых не выходит за эти пределы, считаются приемлемыми, а ошибки, значения которых выходят за эти пределы, сигнализируют о необходимости корректирующих действий.
Существует несколько возможных источников ошибок в прогнозе, включая следующее:
1. Модель может быть неадекватна из-за того, что:
(а) упущена важная переменная;
(б) произошли изменения или смещения переменной, с которыми модель не может справиться (например, внезапное появление тенденции или цикла);
(в) появилась новая переменная (например, новый конкурент).
2. Нерегулярные изменения могут происходить из-за суровых погодных условий или других природных явлений, временной нехватки или перебоев электроэнергии, катастроф и других подобных событий.
3. Может быть неправильно использован метод прогнозирования или неверно интерпретированы результаты.
4. Всегда существуют случайные изменения в данных. Случайность – это неизбежные изменения, которые остаются в данных даже после того, как учтены всевозможные причины изменений.
Обычно прогноз адекватен, когда ошибки вызываются только случайными изменениями. Следовательно, сигналом необходимости пересмотреть действенность определенной методики прогнозирования будет случайность ошибки в прогнозе. Если они не случайны, то необходимо определить, какие источники вызвали эти ошибки и как исправить ситуацию.
Прогнозы можно контролировать, используя контрольные диаграммы или сигналы трекинга. Сигнал трекинга отражает отношение совокупной ошибки прогноза к соответствующему значению MAD:
Сигнал трекинга = (16).
Значения сигнала трекинга сравниваются с определенными пределами, которые основаны на суждении и опыте. Они часто располагаются в диапазоне от ± 3 до ± 8; чаще всего используется значение предела ± 4, которое приблизительно равно границам трех стандартных отклонений. Расположение значений в данном диапазоне позволяет предполагать - но не гарантирует - что прогноз адекватен. После вычисления начального значения MAD, его можно модифицировать с использованием экспоненциального сглаживания.
Использование контрольного графика предусматривает установку верхних и нижних границ для отдельных ошибок прогноза (вместо совокупных ошибок, как в случае с сигналом трекинга). Эти границы кратны квадратному корню из MSE.
Этот метод предполагает следующее:
1) ошибки прогноза произвольно распределены вокруг среднего нулевого значения;
2) распределение ошибок является нормальным.
В сущности, квадратный корень из MSE – это оценка стандартного отклонения в распределении ошибок. Т. о. S= (17).
Для нормального распределения приблизительно 95% значений (в данном случае ошибок) должны попасть в переделы ±2S от нуля, и приблизительно 99% значений должны находиться в пределах 
3S от нуля. Следовательно, если прогноз «под контролем», то 99% или 95% ошибок должны находиться в пределах установленных границ, - 2S или 3S, в зависимости от того, какие пределы используются. Точки, не попавшие в эти пределы, должны быть расценены как доказательство необходимости предпринять корректирующие действия (т. е. прогноз неадекватен).
Графическое отображение ошибок с помощью контрольной диаграммы может быть очень информативно. График помогает наглядно представить процесс и дает возможность проверить присутствие в пределах границ определенных закономерностей – что предполагает возможность усовершенствования прогноза.
Подобно сигналу трекинга, контрольная диаграмма фокусирует внимание на отклонениях, которые выходят за установленные границы. Однако для любого подхода желательно проверить возможные закономерности в ошибках, – даже если ошибки не выходят за установленные границы. Как правило, проверка производится визуально, хотя иногда используются статистические тесты. Если закономерность обнаружена, это значит, что ошибки предсказуемы и, следовательно, неслучайны. То есть прогноз можно улучшить. Например, тенденция в ошибках означает, что ошибки прогрессивно возрастают. Во временном ряде данных может потребоваться прибавление или усиление реакции на тенденцию. В расчетной модели может потребоваться повторное вычисление наклона линии или другая корректировка.
Внесение необходимых изменений в модель прогнозирования даст меньший разброс ошибок прогноза и таким образом, сузит контрольные границы. (Пересмотренные контрольные границы следует вычислять с учетом ошибок прогноза.)
ПРИМЕР 5
Ежемесячная продажа кожаных курток в магазине за последние 24 месяца, прогноз на этот период и его ошибки показаны в приведенной ниже таблице. Определите, работает ли прогноз, используя следующие подходы:
1. Сигнал трекинга, начиная с 10 месяца; MAD модифицируется экспоненциальным сглаживанием. Используйте границы 4 и α = 0,2.
2. Контрольную диаграмму с границами 2S. Чтобы разработать контрольную диаграмму, используйте данные первых восьми месяцев, а затем оцените оставшиеся данные по контрольной диаграмме.
Месяц | А (продажи) | F (прогноз) | A-F (ошибка) | Совокупная
|
1 | 47 | 43 | 4 | 4 |
2 | 51 | 44 | 7 | 11 |
3 | 54 | 50 | 4 | 15 |
4 | 55 | 51 | 4 | 19 |
5 | 49 | 54 | -5 | 24 |
6 | 46 | 48 | -2 | 26 |
7 | 38 | 46 | -8 | 34 |
8 | 32 | 44 | -12 | 46 |
9 | 25 | 35 | -10 | 56 |
10 | 24 | 26 | -2 | 58 |
11 | 30 | 25 | 5 | |
12 | 35 | 32 | 3 | |
13 | 44 | 34 | 10 | |
14 | 57 | 50 | 7 | |
15 | 60 | 51 | 9 | |
16 | 55 | 54 | 1 | |
17 | 51 | 55 | -4 | |
18 | 48 | 51 | -3 | |
19 | 42 | 50 | -8 | |
20 | 30 | 43 | -13 | |
21 | 28 | 38 | -10 | |
22 | 25 | 27 | -2 | |
23 | 35 | 27 | 8 | |
24 | 38 | 32 | 6 |
Решение:
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |
