Прогнозирование спроса и объемов продаж (стр. 2 )

Наивный прогноз может также применяться к ряду, поведение которого показы­вает сезонность или тенденцию. Например, если ежемесячные продажи имеют сезон­ные колебания, то показатель спроса на текущий декабрь может базироваться на пока­зателе спроса за прошедший декабрь, спрос на январь будущего года рассчитывается по спросу за прошлый январь и т. д. Аналогично, если присутствует тенденция к увели­чению (или уменьшению) фактического спроса, то показатели изменения между двумя периодами оцениваются на основе изменений между двумя прошедшими периодами. Например, если спрос в июне на 90 единиц выше, чем в мае, то наивный прогноз на июль, согласно этой тенденции, будет равен фактическому спросу июня плюс допол­нительные 90 единиц. Затем, если спрос в июле был только на 85 единиц больше чем в июне, то прогноз на август будет равен фактическому спросу июля плюс 85 единиц.

Скользящие средние значения. Слабость наивного ме­тода заключается в том, что прогноз просто следует за фактическими данными, с отставанием на один пери­од; он совершенно их не сглаживает. Но данная труд­ность может быть преодолена путем расширения коли­чества данных, на которых построен данный прогноз. Прогноз скользящего среднего значения использует не­сколько самых последних показателей при составлении прогноза.

Прогноз скользящего среднего значения может быть вычислен с использованием следующего уравнения (1):

MAn = 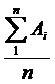(1),

где ί — «Возраст» данных(ί = 1,2,3...);

n — число периодов в скользящем среднем значении;

A— текущее значение с возрастом ί;

MA — прогноз.

Например, МА3 относится к прогнозу скользящего среднего значения с тремя пе­риодами, а МА5 относится к прогнозу скользящего среднего значения с пятью перио­дами.

ПРИМЕР 1

Вычислите скользящее среднее значение за три периода, на основе показателей спроса на стиральные машины для покупок за последние пять периодов.

Решение:

Если фактический спрос в течение периода 6 оказывается 39, то прогноз скользя­щего среднего значения для периода 7 будет таким:

В скользящем среднем значении, при поступлении каждого нового фактического значения, прогноз модифицируется; добавляется самое новое значение и удаляется самое старое, а затем заново вычисляется среднее. Следовательно, прогноз «скользит», отражая только самые последние значения. Скользящее среднее значение может включать столько периодов данных, сколько необходимо. Определяя число периодов, нужно принять во внимание, что число точек, по которым производится усреднение, определяет его чувствительность для каждой новой точки данных: чем меньше показателей усредняется, тем более чувстви­тельно среднее. Если чувствительность важна, то следует использовать скользящее среднее с от­носительно небольшим числом точек. Это обеспечит большую чувствительность, на­пример, к ступенчатым изменениям в данных, но это также сделает прогноз чувстви­тельным даже к случайным изменениям. Наоборот, скользящие средние значения, основанные на большом количестве точек данных, будут больше сглаживать, но мень­ше реагировать на «реальные» изменения. Иными словами, необходимо выбирать между высокой чувствительностью к случайным изменениям данных – и более мед­ленной реакцией на изменения. Преимущество прогноза скользящего среднего значения заключается в том, что его легко рассчитать и легко понять. Возможным недостатком может стать то, что все значения в среднем учитываются на равных. Например, в скользящем среднем значе­нии с 10 периодами, каждое значение имеет вес 1/10. Следовательно, самое старое зна­чение имеет тот же коэффициент значимости, что и самое новое. Если в ряду происхо­дит изменение, то прогноз скользящего среднего значения может реагировать на него достаточно медленно, особенно если имеется большое количество точек усреднения. Уменьшение числа усредняемых значений увеличивает коэффициент значимости более поздних показателей, но это происходит за счет потери потенциальной инфор­мации от более ранних значений.

Взвешенное среднее подобно скользящему среднему значению – за исключением того, что оно придает больший коэффициент значимости самым поздним показа­телям временного ряда. Например, самое позднее значение может иметь коэффициент 0,40, предшествующее ему – 0,30, затем 0,20, и наконец 0,10. Общая сумма баллов должна быть равна 1.

ПРИМЕР 2

Даны следующие показатели спроса (см. таблицу).

а. Рассчитайте прогноз для взвешенного среднего значения, если самому позднему значению присвоен коэффициент значимости 0,40, предшествующему – 0,30, затем 0,20, и 0,10 для самого раннего значения.

б. Если фактический спрос для 6 периода равен 39, составьте прогноз спроса для 7 периода, используя те же самые коэффициенты значимости, что и в пункте а.

Решение:

а. Прогноз = 0,40 (41) + 0,30 (40) + 0,20 (43) + 0,10 (40) = 41,0

б. Прогноз = 0,40 (39) + 0,30 (41) + 0,20 (40) + 0,10 (43) = 40,2

Если используются четыре коэффициента значимости, то для подготовки прогноза используются только четыре самых последних показателя спроса.

Преимущество взвешенного среднего над простым скользящим средним значени­ем состоит в том, что в нем в большей степени учтены именно последние данные. Од­нако выбор коэффициентов значимости до некоторой степени произволен и требует использования метода проб и ошибок для поиска оптимальных соотношений.

Экспоненциальное сглаживание. При экспоненциальном сглаживании каждый новый прогноз основан на предыдущем прогнозе плюс процент разницы между этим прогнозом и фактическим значением ряда в этой точке. Таким образом:

Следующий прогноз = Предыдущий прогноз + (Фактический – Предыдущий прогноз),

где – процент, а (Фактический – Предыдущий прогноз) представляет собой ошибку прогноза. Он изменяется от 0 до 1. Более кратко,

F =F +(A - F ) (2),

где F — прогноз для периода t;

F —прогноз для периода t-1;

— сглаживающая константа;

A — фактический спрос или продажи для периода t – 1.

Константа сглаживания представляет собой процент от ошибки прогноза. Каж­дый новый прогноз равен предыдущему прогнозу плюс процент от предыдущей ошиб­ки. Например, предположим, что предыдущий прогноз был 42 единицы, фактический спрос был 40 единиц, а = 0,10. Новый прогноз вычисляется следующим образом:

F = 42 + 0,10(40-42) = 41,8

Затем, если фактический спрос оказывается 43, следующий прогноз будет:

F = 41,8+ 0,10(43-41,8)= 41,92

Чувствительность корректировки прогноза к ошибке определена константой сглаживания . Чем ближе ее значение к 0, тем медленнее прогноз будет приспосабли­ваться к ошибкам прогноза (т. е. тем больше степень сглаживания). Наоборот, чем ближе значение к 1,00, тем выше чувствительность и меньше сглаживание.

Выбор константы сглаживания – в основном вопрос свободного выбора или ме­тода проб и ошибок. Цель состоит в том, чтобы выбрать такую константу сглажива­ния, чтобы, с одной стороны, прогноз оставался достаточно чувствительным к реаль­ным изменениям данных временного ряда, а с другой – хорошо сглаживал скачки, вызванные случайными факторами. Обычно используемые значения находятся в диапазоне от 0,05 до 0,50.

Некоторые компьютерные программы предусматривают возможность автомати­ческого изменения константы сглаживания, если ошибки прогноза станут неприемле­мо большими.

Экспоненциальное сглаживание – один из наиболее широко используемых мето­дов прогнозирования, частично из-за минимальных требований по хранению данных и легкости вычисления, а частично из-за той легкости, с которой система коэффициен­тов значимости может быть изменена простым изменением значения .

Для получения начального прогноза может быть использован ряд различных под­ходов: среднее нескольких первых периодов, субъективные оценки, или первое факти­ческое значение как прогноз для следующего периода (т. е. наивный подход).

Методы для тенденции

Компонент тенденции во временном ряду отражает эффекты любых долгосрочных факторов в нем. Анализ тенденции включает поиск уравнения, которое соответствую­щим образом опишет тенденцию (принято, что тенденция представлена в данных). Компонент тенденции может быть линейным, параболическим, экспоненциальным и т. д. Рассмотрим исключительно линейную тенденцию, потому что она достаточно часто встречается и с ней легко работать. Существуют два важных метода, которые можно использовать для разработки прогнозов, где присутствует тенденция. Один предполагает использование уравнения тенденции; другой – расширение экспоненциального сглаживания.

Уравнение тенденции. Линейное уравнение тенденции имеет следующий вид:

У = а+bt (3),

где t — определенное число периодов времени от t = 0;

У — прогноз для периода t;

а — значение У при t = 0;

b — наклон линии.

Например, рассмотрите уравнение тенденции У = 45 + 5t. Значение У при t = 0, равно 45, и наклон линии b= 5. Это означает, что в среднем, значение У увеличится на пять единиц для каждого единичного увеличения t. Если t = 10, то про­гноз У будет 45 + 5 (10) = 95 единиц. Уравнение может быть отражено графически, нахождением двух точек на линии. Одна может быть найдена путем подстановки неко­торого значения t в уравнение (например, t = 10), а затем решением его относительно У. Другая точка – а (т. е. У при t =0). Построение этих двух точек и прямой через них, дает нам график линейной тенденции.

Коэффициенты прямой – а и b – могут быть вычислены из статистических данных за определенный период, с использованием следующих двух уравнений:

b=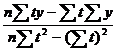 (4),

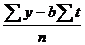a= (5),

где n — число периодов;

у — значение временного ряда.

Экспоненциальное сглаживание тенденций. Разновидность простого экспоненциаль­ного сглаживания может использоваться, когда временной ряд выявляет тенденцию. Эта разновидность называется экспоненциальным сглаживанием, учитывающим тен­денцию или, иногда, двойным сглаживанием. Оно отличается от простого экспоне­нциального сглаживания, которое используется толь­ко тогда, когда данные изменяются вокруг некоторого среднего значения или имеют скачкообразные или по­степенные изменения.

Если ряд выявляет тенденцию и при этом исполь­зуется простое экспоненциальное сглаживание, то все прогнозы будут запаздывать по отношению к тенден­ции. Например, если данные увеличиваются, то каждый прогноз будет занижен. Наоборот, уменьшение данных даст завышенный про­гноз. Графическое отображение данных может показать, когда двойное сглаживание будет предпочтительнее, чем простое.

Скорректированный тенденцией прогноз (the trend-adjusted forecast – TAF) со­стоит из двух элементов: сглаженной ошибки и фактора тенденции.

TAFt+1 = St+Tt (6),

где St — сглаженный прогноз;

Tt — оценка текущей тенденции.

St = TAFt+α1(At - TAFt) (7),

Tt = Tt-1+ α2(TAFt - TAFt-1 - Tt-1) (8),

где α1 и α2 – сглаживающие константы. Двойное сглажива­ние может корректировать изменения в тенденции. Чтобы использовать этот метод, нужно вы­брать значения α1 и α2 (обычно путем подбора) и сделать начальный прогноз и оценку тенденции.

Пример расчета обеими методами показан ниже.

ПРИМЕР 3

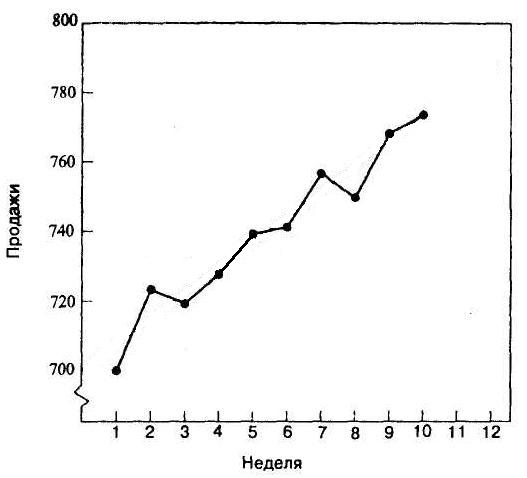
Уровень продаж калькуляторов производства одной корейской компании за последние 10 недель показан в следующей таблице. Отобразите данные таблицы графически, и визуально оцените линейность характера тенденции. Затем опреде­лите уравнение линии тенденции, и предскажите уровень продаж в течение 2-х сле­дующих недель (неделя 11 и неделя 12).

Неделя	Уровень продаж
1	700
2	724
3	720
4	728
5	740
6	742
7	758
8	750
9	770
10	775

Решение:

а. График соответствует линейной тенденции:

Для n = 10: Σ t = 55 и Σ t = 385.

Вычисляем коэффициенты линии тенденции:

b= =7,51

a= =699,4

Таким образом, линия тенденции имеет вид:

У = 699,40 + 7,51t,

где t = 0 для периода 0.

в. Подставляя значения t в это уравнение, вы можете получить прогнозы для буду­щих периодов. Для следующих двух периодов (t = 11 и t = 12), прогнозы таковы:

У = 699,40 + 7,51 (11) = 782,01

У = 699,40 + 7,51 (12) = 789,51

г. Для иллюстрации решения исходные данные, линия тенденции и две проекции (прогноза) показаны на следующем графике:

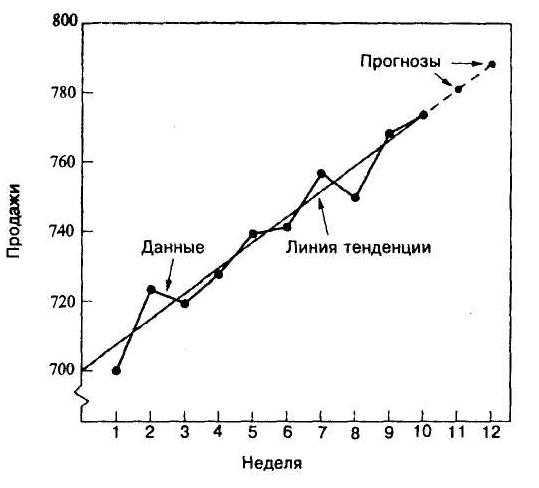
Решим эту задачу через экспоненциальное сглаживание тенденций. Обратите внимание, что начальная оцен­ка тенденции производится по первым четырем значениям.

Оценка тенденции ==9,3

Начальный прогноз (для периода 5) сделан с использованием предыдущего (период 4) значения - 728 плюс на­чальная оценка тенденции:

Начальный прогноз = 728 + 9,3 = 737,3

	Неделя	Уровень продаж	St = TAFt+α1(At - TAFt) Tt = Tt-1+ α2(TAFt - TAFt-1 - Tt-1)
Разви-тие модели	1	700
2	724
3	720
4	728
Испы-тание модели	5	740	738,38=737,3+0,4(740-737,3) 9,3=9,3+0,30
6	742	745,41=747,68+0,4(742-747,68) 9,62=9,3+0,3(747,68-737,3-9,3)
7	758	756,22=755,03+0,4(758-755,03) 8,94=9,62+0,3(755,03-747,68-9,62)
8	750	и т. д.
9	770
10	775	775,91=776,52+0,4(775-776,52) 7,67=7,48+0,3(776,52-768,4-7,48)
Прог - ноз	11		775,91+7,67=783,58

Следовательно прогноз на 11 неделю этим методом будет равен 783,58.

Конечно, прогнозирование методом линейной тенден­ции намного проще, чем с отрегулированными тенденцией прогнозами, и поэтому менеджер должен решить, какие преимущества для него важнее.

Методы для сезонности

Сезонные изменения данных временного ряда – это регулярные восходящие или нисходящие движения в ряду значений, которые можно привязать к периоди­чески повторяющимся событиям.

Сезонность можно отнести к регулярным еже­годным изменениям. Всем знакомы примеры сезон­ности – погодные изменения (например, продажа зимнего и летнего спортивного инвентаря), периоды каникул или отпусков (напри­мер, авиапутешествия, продажа праздничных поздравительных открыток, наплыв ту­ристов в места отдыха и т. д.). Термин «сезонные изменения» также применяется к еже­дневным, еженедельным, ежемесячным и др. регулярно повторяющимся изменениям в данных. Например, в транспорте час пик происходит два раза в день – утром и после полудня. Театры и рестораны часто испытывают еженедельные изменения спроса – ближе к окончанию недели спрос повышается. Банки могут испытывать ежедневные сезонные изменения (более напряженная работа около полудня и перед закрытием), еженедельные (более напряженная работа в конце недели), и ежемесячные (самая на­пряженная работа в конце месяца из-за внесения в кассу или на депозит платежей по социальному обеспечению, платежным ведомостям, пособиям и т. д.). Объем почто­вых отправлений; продажа игрушек, пива, автомобилей и рождественских подарков; за­груженность скоростных автотрасс; регистрация в гостиницах; озеленение и садовод­ство – все это также относится к сезонным изменениям.

Сезонность во временном ряду выражена в количестве, на которое фактические значения отклоняются от среднего значения ряда. Если ряд имеет тенденцию колебать­ся вокруг некоторого среднего значения, то сезонность выражена в показателях этого среднего (или скользящего среднего) значения; если присутствует тенденция, то сезон­ность выражена в показателях тенденции.

Существуют две различных модели сезонности, аддитивная и мультипликатив­ная. В аддитивной модели сезонность выражена как количество (например, 20 единиц), которое добавляется или вычитается из среднего значения ряда. В мультипликативной модели сезонность выражена как процент от среднего количества (например 1,10), который затем умножают на значение ряда, чтобы ввести сезонность. Практически, мультипликативная модель используется намного чаще, чем адди­тивная модель, поэтому мы сосредоточимся исключительно на рассмотрении мульти­пликативной модели.

Сезонные проценты в мультипликативной модели называются сезонными показа­телями или сезонными индексами. Предположим, что сезонный показатель для количе­ства игрушек, проданных в мае, составил 1,20. Это показывает, что продажа игрушек в течение этого месяца была на 20% выше среднемесячного уровня. Сезонный показа­тель из 0,90 для июля показывает, что продажа игрушек в июле составила 90% от сред­немесячной.

Знание сезонных изменений – важный фактор при планировании розничных продаж и составлении календарных планов и графиков. Кроме этого, сезонность может быть важным фактором в планировании производственной мощности для систем, ко­торые разработаны с учетом пиковых загрузок (например, система общественного транспорта, электростанции, скоростные автотрассы и мосты). Знание протяженнос­ти сезонных периодов во временном ряде позволит удалить сезонность из данных (т. е. обрабатывать данные с учетом сезонности), чтобы различить другие закономерности или отсутствие закономерностей в ряде. Простейшая сезонная модель – разновидность наивной методики, описанной для среднего значения. Вместо того, чтобы использовать показатели фактического спроса за последний период, сезонная наивная модель использует для прогноза факти­ческие показатели последнего сезона. Прогноз посещаемости театра вечером данной пятницы равнялся бы посещаемости в последнюю пятницу, следуя сезонной наивной модели, а оценки продаж игрушек в ноябре текущего года могут базироваться на про­даже игрушек в ноябре прошлого года. Если имеют место тенденция и сезонные изменения, то наивная модель включала бы спрос последнего сезона плюс 10%, или любое другое соответствующее увеличение или уменьшение.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4