Урок геометриии в 9 классе по теме
«Вписанная окружность. Урок решения одной задачи».
Святова , учитель математики 1 категории
Цели урока:
- научить учащихся решать задачи на нахождение радиуса вписанной окружности различными способами;
- развивать мыслительную деятельность;
- прививать аккуратность в построении чертежей и последовательность при решении задач.
Ход урока.
I. Фронтальный опрос по изученной теме.
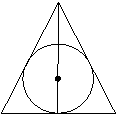
1. Какая окружность называется вписанной в треугольник? В многоугольник?
2. Окружность вписана в треугольник (многоугольник). Как называется в этом случае треугольник (многоугольник)?
3. Какая точка является центром окружности, вписанной в треугольник?
4. Назовите формулу для вычисления площади треугольника, если известен радиус вписанной окружности.
II. Проверка домашнего задания
Один ученик у доски демонстрирует решение задачи № 000, второй - № 000(а)
III. Изучение новой темы.
Сегодня на уроке мы рассмотрим решение задачи на нахождение радиуса вписанной окружности в треугольник различными способами.
Задача № 000 B
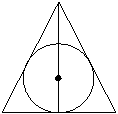 Дано:
Дано:
ΔABC
AB=BC=13
AC=10
Окр (O; r)
Найти: r
A C
H
Учитель выясняет способы решения задачи и по каждому способу приглашает учащегося к доске.
Решение:
1 способ. Используем формулу площади треугольника через радиус вписанной окружности.
![]()
P=AB+BC+AC=13+13+10=36 (см)
![]() , где
, где ![]() .
.
Так как AB=BC, то BH-медиана ![]() AH=HC=
AH=HC=![]() AC=5 (см)
AC=5 (см)
ΔABC, ![]() H=90º, по теореме Пифагора
H=90º, по теореме Пифагора
BH2=AB2-AH2=169-25=144
BH=![]() =12
=12
S=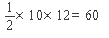 (см2)
(см2)
Получили: 60=![]() *36*r, 60=18*r, r=
*36*r, 60=18*r, r=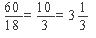 (см)
(см)
2 способ. Свойство биссектрисы треугольника
Сформулируйте свойство биссектрисы треугольника.
B
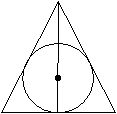 |

O
A C
H
ΔABH, AO-биссектриса![]()
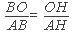
BH – высота, медиана (AB=BC), AH=HC=![]() = 5 см
= 5 см
OH=r
ΔABH, ![]() H=90º по теореме Пифагора
H=90º по теореме Пифагора
BH2=AB2-AH2=144, BH=12
Тогда BO=BH-OH=12-r
Получили: ![]()
(12-к)*5=13r
60-5r=13r
60=18r
r=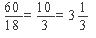 (см)
(см)
3 способ. Подобие треугольников.
 B
B
M
![]()
O
A C
H
OH=OM=r
ΔMBO∞ΔABH (по 2-м углам: ![]() ABH – общий,
ABH – общий, ![]() M=
M=![]() H=90º).
H=90º). ![]()
![]()
BH – высота, медиана (AB=BC) ![]() AH=HC=5 см
AH=HC=5 см
ΔABH, ![]() H=90º по теореме Пифагора
H=90º по теореме Пифагора
BH2=AB2-AH2=144,
BH=12
BO=BH-OH=12-r
Получим: ![]() ; 13r=60-5r
; 13r=60-5r
18r=60
r=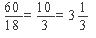 (см)
(см)
4 способ. Определение центра вписанной окружности.
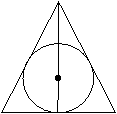 B
B
![]() M
M
 O
O
A C
H
BO, AO – биссектрисы ![]() B и
B и ![]() A треугольника ABC
A треугольника ABC
OM![]() AB, OH
AB, OH AC, OM=OH=r.
AC, OM=OH=r.
BH – высота, медиана (AB=BC) ![]() AH=HC= 5 см
AH=HC= 5 см
ΔABH, ![]() H=90º по теореме Пифагора
H=90º по теореме Пифагора
BH2=AB2-AH2=144,
BH=12
BO=BH-OH=12-r
По свойству касательных AH=AM= 5, тогда MB=AB-AM=13-5=8 см.
ΔMOB, ![]() M=90º по теореме Пифагора
M=90º по теореме Пифагора
BO2=MB2+MO2, (12-r)2=64+r2,
144-24r+r2=64+r2
-24r=-80
r=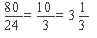 (см)
(см)
IV Самостоятельная работа
Учащиеся получают индивидуальные задания по карточкам на нахождение r вписанной окружности в равнобедренный треугольник. (способ решения учащийся выбирает самостоятельно)
Итог урока.
Д/з. п.74 № 000(и), просмотреть все способы решения задачи и решить задачу одним из понравившихся способов.




