Задание №1. Решение задачи оптимального планирования производства (стр. 1 )

Задание №1. Решение задачи оптимального планирования производства

1.  Цель работы:

Приобретение навыков построения математической модели и решения одноиндексных задач линейного программирования (задача о производстве).

Условие задачи:

Предприятие может изготавливать два вида изделий Р1 и Р2. Запас сырья и затраты на изготовление одного изделия приведены в таблице:

2.  Теоретический материал

2.1. Построение математической модели

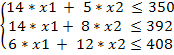
Целевая функция Z=10*x1 + 5*x2 è MAX, при X1, X2 ≥ 0 и X1, X2=целые

2.2. Решение задачи симплексным методом

I этап. Преобразование неравенств в равенства.

Обозначим, yi≥ 0 – выравнивающая (базисная) переменная (i=1,2,3) и добавим эти переменные к левой части неравенств.

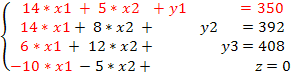
Находим исходное базисное решение: x1 = x2 = 0; y1 = 350; y2 = 392; y3 = 408 ; z=0.

II этап. Выполнение симплексного преобразования.

Шаг 1. Выбираем разрешающий столбец. Он соответствует наименьшему отрицательному элементу в Z-строке. Это число -10, соответствующее 1-му столбцу.

Шаг 2. Выбираем разрешающую строку. Она соответствует наименьшему положительному частному при делении правой части уравнений на значения элементов разрешающего столбца.

Шаг 3. Выбираем разрешающее число. Оно находится на пересечении разрешающей строки и столбца.

Шаг 4. Выполняем симплексное преобразование. Уравнение разрешающей строки делим на разрешающее число. Элементы остальных строк вычисляем по правилу: умножаем уравнение разр. строки на 14, 6 и -10 и вычитаем соответственно из 2-го, 3-го и 4-го уравнений.

Старый элемент - (соответ. число в разр. строке * соответ. число в разр. столбце)/ разр. число

Например, для второй строки, 14 – 14*14/14 = 0;

8 – 5*14/14 =3;

0 – 1*14/14=-1

1 – 0*14/14=1

Запишем полученные уравнения:

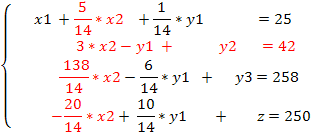
Из полученной системы находим второе базисное решение : x1 = 25; x2 = 0; y1 =0; y2 = 42; y3 = 258 ; z=250.

Шаг 5. Проверка оптимальности плана. Если в Z-строке все элементы неотрицательны, то достигнуто оптимальное решение. В противном случае повторяем все шаги симплексного преобразования.

III этап. Улучшаем план.

Шаг 1. Выбираем разрешающий столбец. Это столбец 2.

Шаг 2. Выбираем разрешающую строку. Это строка 2.

Шаг 3. Выбираем разрешающее число. Это число 3.

Шаг 4. Выполняем симплексное преобразование.

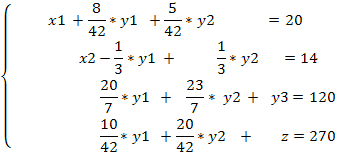
Шаг 5. Проверка оптимальности плана. Так как в Z-строке все элементы неотрицательны, данный план является оптимальным.

Полученное решение : x1 = 20; x2 = 14; y1 =0; y2 = 0; y3 = 0 ; z=270.

3.  Порядок выполнения работы

3.1. Ввод исходных данных в таблицу:

3.2. Ввести формулы для Ограничения ресурса и Целевой функции:

3.3.  Выполнить команду Сервис – Поиск решения:

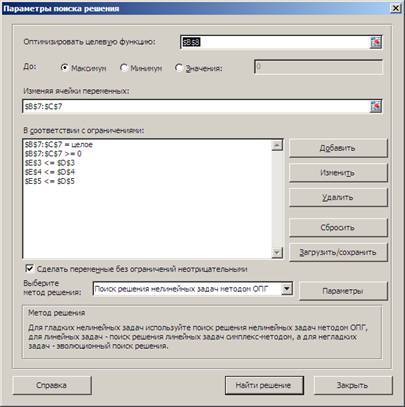
3.4.  Анализ результатов решения:

3.5. Ввести исходные данные и выполнить решение в MathCad:

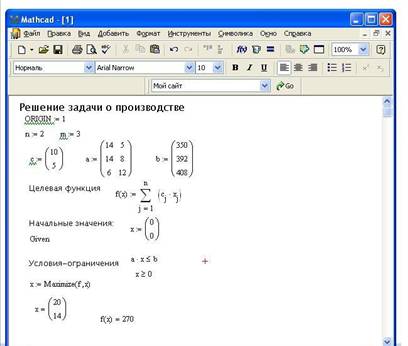
4.  Выводы:

Полученные решения полностью совпадают с расчетом, выполненным симплексным методом.

5.  Варианты задач

Вариант №1

Составить план производства 2-х изделий из сырья 3-х видов. Прибыль от реализации изделий равна 4 у. е. и 8 у. е. Запас сырья составляет 64, 35 и 42 т. Данные приведены в таблице:

Вариант №2

Составить план производства 2-х изделий из сырья 3-х видов. Прибыль от реализации изделий равна 1 у. е. и 2 у. е. Данные о затратах сырья приведены в таблице:

Вариант №3

Для производства четырех видов изделий A1 , A2 , A3 , A4 завод должен использовать три вида сырья I, II, III, запасы которого составляют соответственно 1000, 600 и 150 условных единиц. В таблице приведен расход каждого вида сырья на производство единицы каждого изделия и прибыль от реализации единицы изделия каждого вида.

Вариант №4

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3