Циклическая деградация упругих свойств стали

ЦИКЛИЧЕСКАЯ ДЕГРАДАЦИЯ УПРУГИХ СВОЙСТВ СТАЛИ

, ,

Н-Тагил, Екатеринбург, Россия

В работе [1] предложена объединительная методика оценки ресурса элементов конструкций с неоднородным полем напряжений, основанная на модели циклической деградации статических свойств материала с ростом наработки. В ходе модельного и экспериментального обоснования методики было установлено снижение упругих свойств материала на заключительной стадии циклирования. На примере расчета ресурса пластины с отверстием показывается, что учет данного эффекта приводит к изменению напряженного состояния до появления усталостной трещины и меняет кинетику ее развития.

Для численного решения задачи использовались следующие программные продукты: система пространственного моделирования Solid Works; модуль конечно-элементного анализа COSMOS Works; программа баз данных Microsoft Access; язык программирования Visual Basic for Applications (VBA). Общее количество конечных элементов в модели 10628. Всем конечным элементам задавались одинаковые исходные свойства: 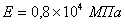- модуль упругости, - коэффициент Пуассона, - предел прочности. Величина силы , при «мягком» нагружении оставалась неизменной и определялась из того условия, чтобы максимальное напряжение по Мизесу в наиболее нагруженном конечном элементе не превышало . Затем выполнялся расчет НДС с определением максимальных напряжений цикла в каждом конечном элементе пластины.

Снижение исходного предела прочности материала SB0 с ростом числа циклов тренировки в каждом конечном элементе определяется зависимостью

,

а условие разрушения элемента

,

где N-число циклов по усталостной кривой для уровня , определяет коэффициент .

:Деградация упругих свойств задавалась аналогичными выражениями: для модуля упругости ,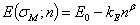

а для коэффициента поперечной деформации

.

В эксперименте упругие свойства менялись медленнее, чем прочностные, поэтому в модельном примере полагалось ; m=2, а значение модуля в момент разрушения составляло 0,2Е. По кривой Веллера записанной в форме

,

где 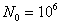- базовое число циклов нагружения, - угол наклона кривой, -предел выносливости материала, находим число циклов до разрушения N на уровне =const. При переходе с одного уровня напряжений на другой использовалось условие эквивалентности двух состояний материала при разной истории нагружения в форме

,

что позволило избежать линейного суммирования повреждений.

На рис.1 приведены результаты расчета сопротивлений материала и напряжений в опасном сечении пластины, параметризованных числом циклов изменения внешней нагрузки

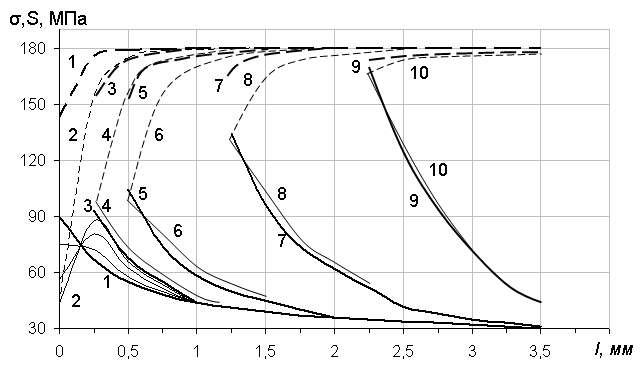Рис.1. Перераспределение напряжений и сопротивлений (штриховые линии) в опасном сечении пластины с ростом циклической тренировки : кривые 1 – при тыс. циклов; кривые 2 – при тыс. циклов; кривые 3 – при 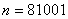; кривые 4 –

при ; кривые 5 – при ; кривые 6 – при ; кривые 7 – при ; кривые 8 – при ; кривые 9 – при ; кривые 10 – при .

До 40 тысяч циклов нагрузки напряжения в опасном сечении мало отличались от исходных. Тогда как сопротивление в наиболее нагруженном элементе на краю отверстия заметно снижалось (кривые 1). Далее распределение напряжений меняется и при 81 000 циклов описывается кривой 2. В этот момент сопротивление крайнего элемента снижается до уровня максимального напряжение цикла, что приводит к усталостному разрушению и перераспределению напряжений при неизменном сопротивлении в уцелевших элементах (кривая 3). Следующий элемент разрушится от усталости при , когда сопротивление в нем снизится до нового уровня напряжений (кривые 4) и трещина скачкообразно подрастет. Предельное состояние равновесия пластины с трещиной длиной 2,25мм отмечено кривыми 10. После 134516 циклов нагрузки трещина динамически пересекает опасное сечение пластины.

Без учета деградации упругих свойств число циклов до появления трещины составляло 62500 циклов, а до разрушения пластины 73 370 циклов. Имеет место существенное расхождение прогнозов долговечности. Приведенный расчет позволяет объяснить различие эффективного и теоретического коэффициентов концентрации напряжений при циклической нагрузке.

ЛИТЕРАТУРА

1., , Лукашук усталостного разрушения пластины с отверстием. - Екатеринбург, Вестник УГТУ-УПИ, №11(82),2006.- С.87-92.