Поле чудес «Математика и математики»

Открытое мероприятие

ПОЛЕ ЧУДЕС «МАТЕМАТИКА И МАТЕМАТИКИ»

Цель: привитие любви к математике, развитие мыслительной деятельности, повышение эрудиции учащихся по различным вопросам из области математики.

Оборудование: выставка книг математической литературы, портреты математиков, наглядный материал (буквы, цифры), плакат с нарисованными кубиками, волчок со стрелкой.

Оформление класса: стенд с книгами, доска с записями, постановка парт в определенном порядке.

Содержание и правила игры. «Поле чудес» - это игра на отгадывание слов. В игре проводятся три тура, в каждом туре участвуют по три игрока. Из каждого тура отгадавшие слово игроки выходят в финал, а отгадавший слово игрок в финале становиться победителем игры.

При выпадении сектора «приз» игрок может взять приз и при этом выбывает из игры, или же, может остаться в игре, отказываясь от приза.

Если будет подсказка, необходимо сменить задание.

На нашем барабане четыре сектора, которые повторятся: приз, ход, переход хода, открой букву. Этого для наших условий достаточно.

На доске.

1. А математику уж затем учить следует, что ум в порядок приводит. ()

2. Природа формирует свои законы языком математики. (Г. Галилей)

3. Математику нельзя изучать, наблюдая, как это делает сосед. (А. Нивен)

Вопрос участникам 1 тура.

Люди научились считать 25-30 тысяч лет тому назад. Сначала они обозначили числа черточками, затем научили называть их, а потом уже придумали цифры и стали выполнять над числами арифметические действия. Они создали разные системы счисления: двоичная система счисления, пятеричная, 7-я система счисления, 10-я система счисления, 12-я система счисления.

Во многих странах даже теперь некоторые товары, например вилки, ножи, ложки продают по 12 штук. В столовый сервиз, как правило, входят 12 глубоких, 12 мелких и 12 маленьких тарелок, а в чайный – 12 чашек, 12 блюдец и т. д.

Как раньше называли число 12? (Дюжина)

Рекламная пауза.

Здесь нужен глаз

На редкость зоркий.

Задача очень не проста:

Четыре цифры на развертке

Поставь на верные места!

На все решенье - пять минут.

Подсказку кубики дают.

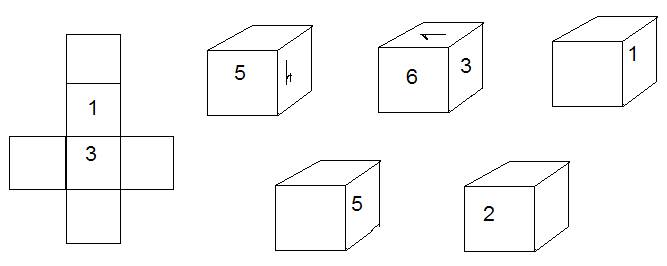
Вопрос участникам 2 тура.

Греческие ученые геометрию считали очень важной наукой. «Математика есть ключ ко всем наукам» - говорили они. И, конечно, они были правы. Ведь все, что можно измерить, выразить числами, становится материалом для применения математики. Наверное, поэтому один знаменитый греческий ученый над дверью дома, в котором он занимался со своими учениками, велел сделать такую надпись: «Не обучившийся геометрии пусть не входит в эту дверь».

Фамилия этого ученого? (Платон)

Рекламная пауза.

Был когда-то веселый миф, который вы, наверное, не раз видели – «В стране не выученных уроков». В нем заядлый лентяй и двоечник попадает в сказочную страну, где живут все его ошибки. В стране невыученных уроков нередко бывали и мы с вами, когда беспомощно плавали у доски, потому что делать уроки казалось нам скучным занятием.

Но скучных предметов не бывает. Мы беремся доказать вам это и приглашаем в путешествие к ее величеству «Математике». Помогут вам в этом самые разные книги и о великих математиках, и о том, как научиться мыслить и решать задачи.

1. Математическая шкатулка.

Здесь вы найдете сведения о великих математиках; представлены здесь и задачи для учащихся 5-9 классов. Задачи и трудные, и замысловатые. Иначе говоря, эта книга является своеобразной математической шкатулкой.

Как пользоваться этой книгой? Прежде всего, попытайтесь сами решить задачи и ответить на вопросы. Может случиться, что задача не будет «поддаваться», тогда загляните в ответы, но не злоупотребляйте этим.

2. За страницами учебника алгебры.

Людей, совершенно неспособных к математике, не бывает, но все же одним она дается легче, чем другим. А вам? Испытать себя в знании математики вам поможет эта книга. Конечно, как и всякая книга по математике, она нелегка, но читайте ее не торопясь, заглядывая в учебники по алгебре и геометрии, повторяйте забытое.

3. , За страницами учебника математики.

Книга поможет повторить и расширить знания по математике. Начинается она с рассказа – как научились люди считать, когда и где возникли единицы измерения. К каждой главе даны задачи, чтобы справиться с ними, нужно проявить смекалку, настойчивость и целеустремленность.

4. Никольский, Потапов и др. Арифметика

Данная книга может быть полезна тому, кто желает привести в порядок знания по математике.

5. Никольская, Семенов. Учимся рассуждать и доказывать.

Что значит рассуждать правильно? Как находить истину? Ответ на этот вопрос будет длительным. Вы можете получить его прочитав книгу до конца. Понять истину вам помогут школьники Петя и Катя и их сосед – студент Митя – герои нескольких историй, о которых рассказывается в книге.

Вопрос участникам 3 тура.

Много веков мечтали люди создать машины, которые бы сами выполняли порученные им работы – ткали и пряли, ковали и вытачивали. Чтобы создать такие машины-автоматы понадобились устройства, умеющие выполнять арифметические операции, понимать и перерабатывать различные сведения. Сейчас машины-математики применяются во всех областях человеческой деятельности. В нашей стране первая ЭВМ была построена в 1951 году.

Под чьим руководством построена эта машина? ( 1902 – 1974)

Рекламная пауза

Часто знает и дошкольник,

Что такое треугольник.

А уж вам-то как не знать,

Но совсем другое дело –

Быстро, точно и умело

Треугольники считать.

Например, в фигуре этой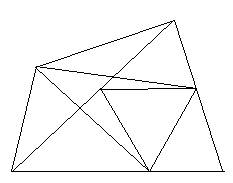

Сколько разных? Рассмотри!

Все внимательно исследуй

И по краю, и внутри!

Игра со зрителями.

Название «ромб» происходит от греческого слова, обозначавшего детскую игрушку. На эту игрушку ромб становится похож, если поставить его на острый угол.

Какая это игрушка? (Волчок)

Вопрос участникам финальной игры.

Удивительный случай произошел в детстве с одной из самых знаменитых женщин-математиков . Когда в доме ее отца шел ремонт, на детскую комнату не хватало обоев. Эта комната простояла несколько лет, оклеенная лишь простой бумагой. Но по счастливой случайности на эту предварительную оклейку пошли записи лекций по высшей математике, которые читал один из крупнейших русских ученых 19-ого века в Петербургской Академии наук.

Листы, исписанные странными, непонятными формулами, обратили на себя внимание маленькой Сони. Целые часы проводила около стен детской комнаты, пытаясь понять порядок, в котором шли листы, и прочесть написанный на них текст. От этого внешний вид многих формул врезался в ее память, да и сопровождавшие их слова запомнились ей, хотя она и не могла тогда понять их смысла. Но когда через несколько лет пятнадцатилетняя Соня брала первые уроки высшей математики, ее преподаватель удивлялся, как скоро она усвоила сложнейшие понятия этой науки. А дело было в том, что в ту минуту, когда он объяснял ей эти понятия, девочка вдруг вспоминала слова из лекций ученого, которые она когда-то заучивала, глядя на стены своей комнаты.

Чьи лекции это были, как фамилия этого ученого? ()

Суперфинал (вопрос для победителя финальной игры)

Какая геометрическая теорема в старину называлась теоремой невесты? (теорема Пифагора)

Запасные вопросы

1. В древности вавилоняне использовали метод приближенного извлечения квадратного корня, который состоял в следующем. Пусть а – некоторое натуральное число, не являющееся полным квадратом. Представим а в виде суммы в+с, где с достаточно мало с в. Тогда

=в + . Указанный метод извлечения квадратного корня подробно описан древнегреческим ученым в 1 в. Н. э.

Фамилия этого ученого? (Герон)

2.В учебниках геометрии с самого начала говорится о точках и прямых, т. е. выбирают основные понятия, им не дают определений, затем формулируют аксиомы, их не доказывают, а уж потом строятся определения, доказываются теоремы, опираясь на основные понятия и аксиомы. Так создается теория, на основе которой решатся практические задачи,- ведь аксиомы взяты из практики, из обобщенного человеческого опыта. И получается геометрия – красивая, не очень легкая наука, построенная, как обычно говорят, «дедуктивно», т. е. «выведенная из аксиом и основных понятий».

Именно так строил свое знаменитое произведение-сочинение Евклид. Именно поэтому эта книга долгие годы служила образцом математического сочинения и основой для изучения математики.

Как называется эта книга? («Начала». В современном издании эта книга имеет более 500 страниц)

Вывод: такая форма работы способствует формированию самостоятельности, развитию мышления, математической эрудиции, развитию творческих навыков, расширят рамки школьного учебника. Учитель для себя выявляет наиболее способных для индивидуальной работы.