Методическое указание к лабораторной работе по теме: «Решение однородной минимаксной задачи генетическими алгоритмами: моделью Холланда, моделью Голдберга и их модификациями с использованием поколенческой стратегии»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ДГТУ)

Кафедра «Программное обеспечение вычислительной техники и автоматизированных систем»

Методическое указание к лабораторной работе по теме:

«Решение однородной минимаксной задачи генетическими алгоритмами: моделью Холланда, моделью Голдберга и их модификациями с использованием поколенческой стратегии»

Ростов-на-Дону

2014 г

1. Общие сведения

Предметом области исследования расписаний является круг задач проектирования и организационного управления в различных системах, в которых требуется найти наилучшее (оптимальное) значение выбранных критериев их функционирования с учетом имеющихся ограничений.

В данном руководстве будут рассмотрены классические генетические алгоритмы (ГА) Холланда и Голдберга и их модификации с использованием поколенческой стратегии для решения задачи получения расписания в однородной вычислительной системе.

В качестве основного критерия рассматривается минимаксный критерий, который минимизирует максимальное время окончания работы программ.

2. Постановка задачи

Имеется вычислительная система (ВС), состоящая из несвязанных идентичных устройств (приборов, процессоров и т. п.):

.

На обслуживание в ВС  поступает набор из независимых параллельных заданий (работ) , известно время решения задания на любом из устройств. При этом каждое задание может выполняться на любом из устройств (процессоре), в каждый момент времени отдельный процессор обслуживает не более одного задания и выполнение задания не прерывается для передачи на другой процессор. Требуется найти такое распределение заданий по процессорам, при котором суммарное время выполнения заданий на каждом из процессоров было бы минимальным. Под расписанием следует понимать отображение , такое что, если , то говорят что задание , в расписании назначенного на процессор . При сделанных выше допущениях, расписание можно представить разбиением множества заданий на непересекающихся подмножеств .

Критерий, используемый для минимизации времени завершения обслуживания заданий, является минимальным критерием и определяется в следующем виде: ,  где  - время завершения работы процессора .

3. Генетические алгоритмы

Для решения поставленной задачи рассматриваются следующие алгоритмы:

3.1 Модель Холланда

Модель Холланда является классической моделью генетического алгоритма. Модель Холланда можно отразить в виде последовательности шагов:

Шаг 1.  Формируется  начальное поколение, состоящее из заданного числа особей.

Шаг 2.  Пропорциональный отбор особей и применение ГА операторов кроссовера и мутации с заданной вероятностью для создания нового поколения.

Шаг 3.  Проверка условия останова, которая обычно заключается в неизменности лучшего решения в течение заданного числа поколений. Если проверка прошла не успешно, то переход на шаг 2.

Шаг 4.  Лучшая особь выбирается как найденное решение.

3.2 Модель Голдберга

Модель Голдберга отличается от модели Холланда, тем, что использует турнирный отбор особей в новое поколение, который улучшает результаты алгоритма. Турнирный отбор может быть описан следующим образом: лучший потомок, полученный при кроссовере, сравнивается с особями в поколении, и если существует особь, значение которой хуже, то потомок занимает ее место. Если же такой особи нет, то потомок уничтожается.

Так же модель Голдберга можно отразить в виде последовательности шагов:

Шаг 1.  Формируется  начальное поколение, состоящее из заданного числа особей.

Шаг 2.  Турнирный отбор особей и применение ГА операторов кроссовера и мутации с заданной вероятностью для создания нового поколения.

Шаг 3.  Проверка условия останова, которая обычно заключается в неизменности лучшего решения в течение заданного числа поколений. Если проверка прошла не успешно, то переход на шаг 2.

Шаг 4.  Лучшая особь выбирается как найденное решение.

3.3 Модификации генетических алгоритмов с использованием поколенческой стратегии отбора особей в новое поколение

       Иногда для достижения лучшего результата полезно варьировать размер популяции, то есть количество особей может быть не только постоянным, но и переменным. Применительно к рассматриваемой задаче в модификациях алгоритмов Холланда и Голдберга используем базовые изменения количества особей в поколении по следующим схемам:

Схема поколенческой стратегии формирования нового поколения 1-2:

1) В первом поколении задавалось количество особей .

2) Во втором поколении генерировалось в два раза больше особей, чем в первом поколении.

3) В третьем поколении происходил возврат к исходному количеству особей .

Процесс продолжался до тех пор, пока значение критерия не повторится заданное количество раз.

Схема отражена на рисунке П. З.1.

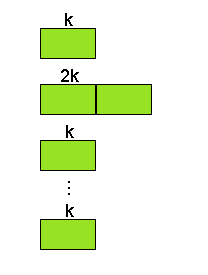
1 – Схема поколенческой стратегии 1-2

Схема поколенческой стратегии формирования нового поколения 1-2-3:

1) В первом поколении задавалось количество особей .

2) Во втором поколении генерировалось в два раза больше особей, чем в первом поколении.

3) В третьем поколении генерировалось в три раза больше особей, чем в первом поколении.

4) В четвертом поколении происходил возврат к исходному количеству особей .

Процесс продолжался до тех пор, пока значение критерия не повторится заданное количество раз.        

Схема отражена на рисунке П. З.2.

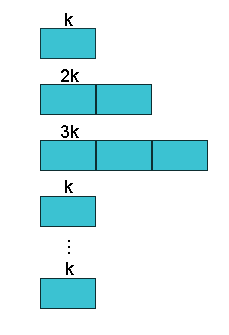
2 – Схема поколенческой стратегии 1-2-3

4. Варианты заданий

Задание определяется согласно № - номера студента в списке, по приведенным ниже таблицам (табл. П. З.1, табл. П. З.2). Алг. - алгоритм, который необходимо запрограммировать. Параметр n-определяет число устройств, m – количество работ, T – множество весов работ, случайным образом берется m работ в пределах, указанных в таблицах П. З.1 и П. З.2.

Например, если студент в списке под номером №9, то Алг. = «Модель Холланда, схема поколенческой стратегии 1-2-3», то есть необходимо запрограммировать классическую модель Холланда и ее модификацию с использованием схемы поколенческой стратегии 1-2-3, n = 4, m = 23, T формируется из m работ, вес которых выбирается случайным образом в отрезке [25-35].

1  – Варианты заданий 1-12

2 – Варианты заданий 13-24

5. Литература

1. “Теория расписания и вычислительные машины” – M.: “Наука”, 1987.

2. , , Базы данных. Интеллектуальная обработка информации. – М.: «Нолидж», 2000.

3. , , Сравнительные характеристики модификации модели Холланда при поколенческой стратегии (статья) - Труды Северо-Кавказского филиала Московского технического университета связи и информатики - Ростов-на-Дону.: ПЦ «Университет» СКФ МТУСИ, 2014. – Ч. 1.