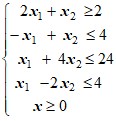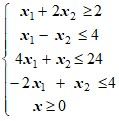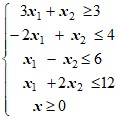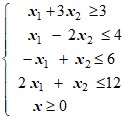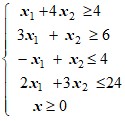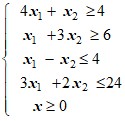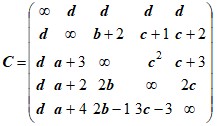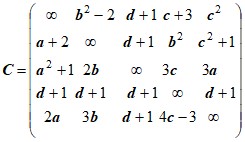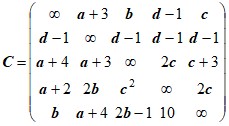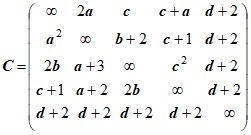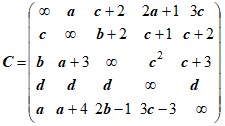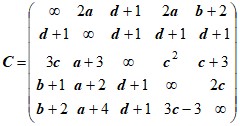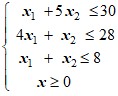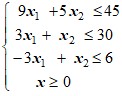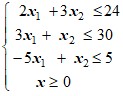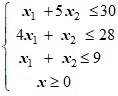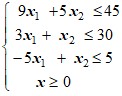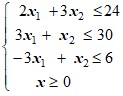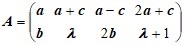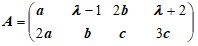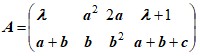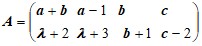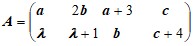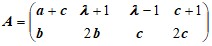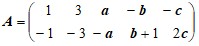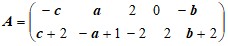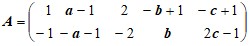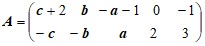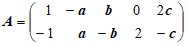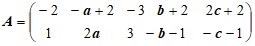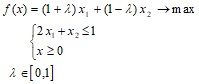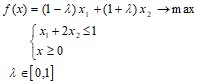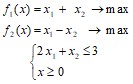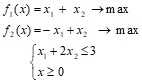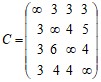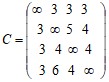МИНОБРНАУКИ РФ
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
«Южный федеральный университет»
Факультет математики, механики и компьютерных наук
Рассмотрено и рекомендовано на заседании кафедры высшей математики исследования операций ЮФУ Протокол №_1___________ "__30___"___августа_______2011г. Зав. кафедрой ________________ | УТВЕРЖДАЮ Декан факультета (зам. декана по учебной работе) ___________________ "____"____________2011 г. |
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
учебной дисциплины "Теория игр и исследование операций "
вузовского компонента цикла по специальности прикладная математика
и информатика
Семестр 6
Всего часов –68, из них – лекции 34,
–самостоятельная работа 34 час.
Отчетность по курсу – зачёт
Составитель: доц.
Утвержден Советом Южного федерального университета
Протокол №_____ от «______» _________ 2011г.
Ростов-на-Дону
2011
Пояснительная записка к рабочей программе по дисциплине
"Исследование операций "
В курсе рассматриваются методы параметрического, целочисленного и динамического программирования, а также вероятностные модели, используемые для анализа систем со случайным поведением и принятия соответствующих решений. Курс ориентирует студентов на решение практических задач, которые можно описать с помощью той или иной математической модели с целью получения оптимального решения. Курс является пособием по теории и практическому использованию методов исследования операций. В курсе представлены важгнейшие разделы исследования операций: теория принятия решений, теория игр, теория массового обслуживания и теория графовБ имитационное моделирование.
Цели преподавания.
Дать студентам фундаментальные знания по исследованию операций, познакомить с основными принципами динамического программирования и оптимизационными задачами на графах, с Марковскими процессами и с системами массового обслуживания; обучить их теоретическим методам решения некоторых классов задач и основным численным методам расчета оптимальных управлений.
РАБОЧАЯ ПРОГРАММА КУРСА
“ Исследование операций “
Лекций - 34 час
Тема 1. «Введение» 2 час
Предмет и история развития исследования операций (ИО), основные принципы и подходы. Основные этапы операционного исследования. Простейшие задачи ИО. История ИО. ИО как современная форма системного анализа. Многоэтапность и неоднозначность постановки задач. Техника упрощения задач - на примере управления левитацией.
Тема 2. «Параметрическое линейное программировани» 2 час
Постоптимальный анализ задач линейного программирования. Метод линейного параметрического программирования.
Тема 3. «Модели исследования операций на графах» 6 час
Кратчайший остов и путь. Абсолютный центр. Задача об оптимальном назначения. Поток в сети. Лемма о величине потока. Теорема Форда-Фалкерсона. Алгоритм Форда-Фалкерсона. Задачи, сводимые к задаче нахождения максимального потока: задача с несколькими источниками и стоками, задача о спросе и предложении.
Тема 4. «Сетевые модели» 2 час
Критический путь и резервы работ. Использование принципов динамического программирования.
Тема 5. «Календарное планирование» 4 час Дискретные модели задачи ИО. Общая схема метода "ветвей и границ". Задача коммивояжера. Метод "ветвей и границ" для ее решения. Задача о 3-х станках.
Тема 6. «Игровые модели исследования операций» 4 час
Элементы теории матричных игр. Матричные игры. Оптимальные стратегии. Разрешимость игр в частных стратегиях. Смешанные стратегии. Теорема Нэша. Графический способ решения игр. Сведение матричных игр к задачам линейного программирования.
Тема 7. «Стохастическое линейное программирование» 1 час Подходы к решению задач стохастического ЛП. Сравнение подходов.
Тема 8. «Многокритериальные задачи» 3 час
Постановка задачи. Множество Парето. Интерактивный анализ аддитивной функции полезности. Различные подходы к задачам многокритериальной оптимизации. Свертка критериев. Построение множества Парето. Метод ранжирования критериев. Метод идеальной точки.
Тема 9. «Случайные Марковские процессы» 4 час
Стохастические процессы. Марковские цепи. Уравнение Чепмена-Колмогорова для вероятностей состояний. Предельные вероятности. Простейший поток событий. Задача садовника и динамическое программирование.
Тема 10. «Системы массового обслуживания» 4 час
Классификация систем и их характеристики. Одноканальная система с потерями. Многоканальная система с потерями. Одноканальная система с очередью. Многоканальная система с очередью.
Тема 11. «Имитационное моделирование» 2 час
Имитационное моделирование. Функции, задачи и возможности его. Исследование систем массового обслуживания с помощью имитационных моделей.
Л и т е р а т у р а
1. Вентцель операций. Задачи, принципы, методология.- М.: Высш. шк.,2001.
2. ведение в исследование операций. - Минск:Вильямс,2001.
3. ведение в исследование операций. Т.1 -2. – М., 1985.
4. , Суворов операций в экономике: модели, задачи, решения: Учеб. Пособие. – М.: ИНФА-М, 2003
5. сновы исследования операций, т.1-3. М:,Мир, 1973.
6. ,Жак операций. Изд-во МГУ, 1980.
7. и др. Линейное программирование и смежные вопросы.
Часть 1-12. Мет. указания. УПЛ РГУ 1998-2004 г.
8. , , . Теория массового
обслуживания (часть 1,2): Метод. указания для студентов экономического
факультета по курсу “Математические методы исследования операций”-
Ростов н/Д: РГУ, 2004 г.
9. ,Землянухина в сетях. Часть 1-4. Мет. указания. УПЛ
РГУ 1987-1989 г.
Дополнительная литература
1. Исследование операций. Под редакцией Дж. Моудера. 1981
2. Исследование операций, 1990
3 , Юдин направления в линейном
прораммировании. М:,Сов. Радио,1966
Самостоятельная работа
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 1
по курсу "ИССЛЕДОВАНИЕ ОПЕРАЦИЙ"
для студентов специальности "Прикладная математика"
3-го курса мех.-мат. ф-та, 2005 г.
1. Решить задачу параметрического линейного программирования
(2-мя способами - графически и с применением симплекс-метода)
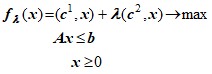
при изменении параметра λ в пределах [λ’,λ’’]. Построить график функции ![]() и найти ее минимум.
и найти ее минимум.
Д а н н ы е к з а д а ч е 1.
Варианты ограничений задачи:
1 |
| 2 |
|
3 |
| 4 |
|
5 |
| 6 |
|
Варианты вектора ![]() :
:
![]()
![]()
![]()
![]()
1 | (3,1) | (-1,1) | 4 | (1,3) | (1,-1) |
2 | (3,2) | (-2,1) | 5 | (2,5) | (1,-2) |
3 | (1,1) | (-3,2) | 6 | (4,5) | (3,-3) |
Варианты диапазона [λ’,λ’’]:
1) [-140,33] 2) [-20,180] 3) [0,290] 4) [-170,30]
5) [-30,160] 6) [-50,220]
Вариант задания выбирается студентом следующим образом: пусть N – номер, выданный студенту преподавателем. Разложить его по основанию 6,т. е. ![]() .
.
Тогда - вариант ограничений задачи: ![]()
- вариант вектора ![]() :
: ![]()
- вариант диапазона [λ’,λ’’] :
Литература
и др. Линейное программирование и смежные вопросы. Часть 4.Мет. указания. УПЛ РГУ 1998 г.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 2
по курсу "ИССЛЕДОВАНИЕ ОПЕРАЦИЙ"
для студентов специальности "Прикладная математика"
3-го курса мех.-мат. ф-та, 2006 г.
1. Найти максимальный стационарный поток и минимальный разрез в орсети G=(X, U), заданной списком дуг, из источника 1 в сток 7 при заданной функции c:U->R пропускных способностей дуг и при заданном начальном потоке f0.
Д а н н ы е к з а д а ч е 1.
Варианты списка дуг:
Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | ||||||
1 | (1,2) | 1 | (1,2) | 1 | (1,2) | 1 | (1,2) | 1 | (1,2) | 1 | (1,2) |
2 | (1,3) | 2 | (1,3) | 2 | (1,3) | 2 | (1,3) | 2 | (1,3) | 2 | (1,6) |
3 | (2,3) | 3 | (1,4) | 3 | (2,3) | 3 | (2,3) | 3 | (1,4) | 3 | (2,3) |
4 | (3,2) | 4 | (3,2) | 4 | (3,2) | 4 | (3,2) | 4 | (1,5) | 4 | (3,2) |
5 | (2,4) | 5 | (2,3) | 5 | (2,4) | 5 | (2,4) | 5 | (2,3) | 5 | (2,4) |
6 | (4,2) | 6 | (2,5) | 6 | (2,5) | 6 | (2,5) | 6 | (3,2) | 6 | (2,6) |
7 | (2,5) | 7 | (3,4) | 7 | (3,5) | 7 | (5,2) | 7 | (2,6) | 7 | (4,3) |
8 | (3,4) | 8 | (4,3) | 8 | (3,6) | 8 | (3,6) | 8 | (4,3) | 8 | (3,4) |
9 | (4,3) | 9 | (3,5) | 9 | (6,3) | 9 | (6,3) | 9 | (3,4) | 9 | (3,7) |
10 | (3,6) | 10 | (3,6) | 10 | (4,5) | 10 | (3,4) | 10 | (3,6) | 10 | (5,4) |
11 | (4,5) | 11 | (4,6) | 11 | (5,4) | 11 | (4,5) | 11 | (6,3) | 11 | (4,5) |
12 | (4,6) | 12 | (6,4) | 12 | (4,7) | 12 | (4,6) | 12 | (4,5) | 12 | (4,7) |
13 | (6,4) | 13 | (6,5) | 13 | (6,5) | 13 | (6,5) | 13 | (5,4) | 13 | (6,5) |
14 | (5,6) | 14 | (5,6) | 14 | (5,6) | 14 | (5,6) | 14 | (5,6) | 14 | (5,6) |
15 | (5,7) | 15 | (5,7) | 15 | (5,7) | 15 | (5,7) | 15 | (5,7) | 15 | (5,7) |
16 | (6,7) | 16 | (6,7) | 16 | (6,7) | 16 | (6,7) | 16 | (6,7) | 16 | (6,7) |
Варианты функции пропускных способностей:
Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | ||||||
1 | 9 | 1 | 10 | 1 | 7 | 1 | 11 | 1 | 11 | 1 | 12 |
2 | 8 | 2 | 9 | 2 | 8 | 2 | 10 | 2 | 10 | 2 | 10 |
3 | 9 | 3 | 8 | 3 | 8 | 3 | 9 | 3 | 9 | 3 | 10 |
4 | 4 | 4 | 9 | 4 | 9 | 4 | 9 | 4 | 8 | 4 | 11 |
5 | 3 | 5 | 4 | 5 | 4 | 5 | 5 | 5 | 4 | 5 | 3 |
6 | 2 | 6 | 2 | 6 | 3 | 6 | 6 | 6 | 4 | 6 | 3 |
7 | 3 | 7 | 4 | 7 | 2 | 7 | 6 | 7 | 4 | 7 | 2 |
8 | 4 | 8 | 5 | 8 | 2 | 8 | 7 | 8 | 5 | 8 | 3 |
9 | 5 | 9 | 4 | 9 | 3 | 9 | 5 | 9 | 5 | 9 | 4 |
10 | 4 | 10 | 3 | 10 | 4 | 10 | 5 | 10 | 4 | 10 | 5 |
11 | 3 | 11 | 6 | 11 | 4 | 11 | 6 | 11 | 3 | 11 | 4 |
12 | 3 | 12 | 3 | 12 | 3 | 12 | 5 | 12 | 2 | 12 | 5 |
13 | 4 | 13 | 4 | 13 | 9 | 13 | 6 | 13 | 2 | 13 | 6 |
14 | 8 | 14 | 9 | 14 | 8 | 14 | 10 | 14 | 10 | 14 | 10 |
15 | 9 | 15 | 10 | 15 | 8 | 15 | 9 | 15 | 11 | 15 | 11 |
16 | 9 | 16 | 8 | 16 | 7 | 16 | 9 | 16 | 11 | 16 | 11 |
Варианты начального потока:
Начальный поток определяется следующими правилами: на каждой дуге пары (i, j) и (j, i)
поток равен ![]() , на остальных дугах поток равен 0
, на остальных дугах поток равен 0
1. A=1 2. A=2 3. A=3 4. A=4
Вариант задания выбирается студентом следующим образом: пусть N – номер, выданный студенту преподавателем. Разложить его по основанию 6,т. е. ![]() .
.
Тогда - вариант списка дуг: ![]()
- вариант функции пропускных способностей : ![]()
- вариант начального потока : ![]() .
.
Литература
,Землянухина в сетях. Часть 1. Мет. указания. УПЛ РГУ 1987 г.ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 3
по курсу "ИССЛЕДОВАНИЕ ОПЕРАЦИЙ"
для студентов специальности "Прикладная математика"
3-го курса мех.-мат. ф-та, 2005 г.
Задача коммивояжера. Найти в графе, заданном матрицей C весов дуг, гамильтонов контур минимального веса, используя метод ветвей и границ.Д а н н ы е к з а д а ч е 1.
Варианты матрицы C
1 |
| 4 |
|
2 |
| 5 |
|
3 |
| 6 |
|
Варианты параметра d:
1. d=3 2. d=4 3. d=5 4. d=6 5. d=7 6. d=8
Варианты параметров a, b,c:
a=d+5 ; b=d-1; c=d+2. a=d+4 ; b=d+1; c=d-1. a=d+3 ; b=d+3; c=d+1. a=d+6 ; b=d+2; c=d+3.Вариант задания выбирается студентом следующим образом: пусть N – номер, выданный студенту преподавателем. Разложить его по основанию 6,т. е. ![]() .
.
Тогда - вариант матрицы C: ![]() ; вариант параметра d :
; вариант параметра d : ![]() ;
;
- вариант параметров a, b,c : ![]() .
.
2. Решить двухкритериальную задачу вида (графически) [1]:
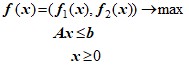
Построить множество Парето.
Д а н н ы е к з а д а ч е 2.
Варианты ограничений:
1 |
| 3 |
| 5 |
|
2 |
| 4 |
| 6 |
|
Варианты функции ![]() :
:
1. ![]() 2.
2. ![]()
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]()
Варианты функции ![]() :
:
1. ![]() 2.
2. ![]() 3.
3. ![]()
4. ![]()
Вариант задания выбирается студентом следующим образом: пусть N – номер, выданный студенту преподавателем. Разложить его по основанию 6,т. е. ![]() .
.
Тогда - вариант ограничений: ![]() ; вариант функции
; вариант функции ![]() :
: ![]() ;
;
- вариант функции ![]() :
:![]() .
.
3. Матричная игра[2].
А) Определить, при каких значениях параметра λ матричная игра с платежной матрицей A размера 2×4 имеет решение в чистых стратегиях. Найти это решение.
Д а н н ы е к з а д а ч е 3(А).
Варианты матицы A:
1 |
| 4 |
|
2 |
| 5 |
|
3 |
| 6 |
|
Варианты a, c:
1. a=4, c=3; 2. a=5, c=3; 3. a=6, c=5;
4. a=7, c=4; 5. a=8, c=3; 6. a=8, c=6.
Варианты b:
1. b=6 2. b=7 3. b=8 4. b=9
Вариант задания выбирается студентом следующим образом: пусть N – номер, выданный студенту преподавателем. Разложить его по основанию 6,т. е. ![]() .
.
Тогда - вариант матрицы: ![]() ; вариант a, c :
; вариант a, c :![]() ;
;
- вариант b: ![]() .
.
Б) Решить графически и симплекс-методом матричную игру с платежной матрицей A размера 2×5.
Д а н н ы е к з а д а ч е 3(B).
Варианты матицы A:
1 |
| 4 |
|
2 |
| 5 |
|
3 |
| 6 |
|
Варианты b, c:
1. b=4, c=3; 2. b=5, c=3; 3. b=6, c=5;
4. b=1, c=2; 5. b=2, c=3; 6. b=4, c=5.
Варианты a:
1. a=6 2. a=7 3. a=4 4. a=5
Вариант задания выбирается студентом следующим образом: пусть N – номер, выданный студенту преподавателем. Разложить его по основанию 6,т. е. ![]() .
.
Тогда - вариант матрицы: ![]() ; вариант b, c :
; вариант b, c :![]() ;
;
- вариант a: ![]() .
.
Литература
и др. Линейное программирование и смежные вопросы. Часть 8-9. Мет. указания. УПЛ РГУ 1998 г. и др. Линейное программирование и смежные вопросы. Часть 5.Мет. указания. УПЛ РГУ 1998 г.
Перечень вопросов, выносимых на зачет.
1.Предмет и история развития исследования операций (ИО), основ-
ные принципы и подходы. Основные этапы операционного исследо-
вания.
2.Постоптимальный анализ задач линейного программирования.
Параметрическое линейное программирование.
3.Кратчайший остов и путь. Задача об оптимальном назначении.
4.Поток в сети..Теорема Форда-Фалкерсона. Алгоритм Форда-Фалкерсона.
Задача о спросе и предложении.
5.Сетевые модели. Критический путь и резервы работ.
6.Задача коммивояжера. Метод "ветвей и границ" для ее решения. Задача о 3-х
станках
7. Матричные игры. Графический способ решения игр. Сведение матричных
игр к задачам линейного программирования.
8.Многокритериальные задачи. Множество Парето. Свертка критериев. Построение
множества Парето. Метод ранжирования критериев.
9.Стохастические процессы. Марковские цепи. Уравнение Чекмена-Колмо-
горова для вероятностей состояний. Предельные вероятности. Задача садовника
10.Системы массового обслуживания. Одноканальная система без очереди.
Многоканальная система без очереди. Одноканальная система с
очередью.
Билеты к зачету
Билет 1 | Билет 2 |
1. Решить задачу ЛПП | 1. Решить задачу ЛПП |
2. При какой интенсивности б | 2. При какой интенсивности б |
3. Дана орсеть списком дуг и пропускных способностей: Дуга прор. сп. Дуга прор. сп. (1,2) 4 (1,3) 3 (2,3) 3 (3,2) 4 (2,4) 2 (3,4) 4 Исходный поток на всех дугах равен 2. Найти максимальный поток. | 3. Дана орсеть списком дуг и пропускных способностей: Дуга прор. сп. Дуга прор. сп. (1,2) 3 (1,3) 4 (2,3) 4 (3,2) 3 (2,4) 4 (3,4) 2 Исходный поток на всех дугах равен 1. Найти максимальный поток. |
4. Решить матричную игру графически, если платежная матрица задана: | 4. Решить матричную игру графически, если платежная матрица задана: |
5. Решить задачу: | 5. Решить задачу: |
6. Дана задача коммивояжера с матрицей: Сделать два последовательных ветвления по методу ветвей и границ. | 6. Дана задача коммивояжера с матрицей: Сделать два последовательных ветвления по методу ветвей и границ. |