Обработка эмпирических данных исследования (стр. 4 )

Рассмотрим пример построения функции нормального распределения для интервального вариационного ряда (табл. 5.6):

Таблица 5.6

Распределение семей по общей площади их жилья

Теоретические частоты ряда для кривой нормального распределения рассчитаны по формуле (5.11). Значения средней арифметической и среднего квадратического отклонения для данной кривой (рис. 5.5) составили 58,1 и 18,6 соответственно. Эти значения рассчитаны по формулам (5.3) и (5.5) по измеренному вариационному ряду. Как следует из табл. 5.6, теоретические частоты (приводятся значения, округленные до целых чисел) близки к эмпирическим частотам, хотя имеются некоторые расхождения.

Оценим количественно близость полученных частот с помощью критерия Пирсона (). Он представляет собой сумму отношений квадратов разности между эмпирическими () и теоретическими () частотами к теоретическим частотам:

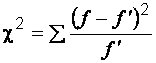.  (5.10)

Значение критерия Пирсона для рассматриваемого примера составляет 8,6. Полученное значение следует сравнить с критическим, определяемым по специальным таблицам (см. [5]), исходя из принимаемого уровня значимости и числа степеней свободы. Установлено, что при числе степеней свободы, равном 7 (из количества интервалов вычитается число 3) и уровне значимости, равном 5 %, критическое значение критерия  составляет 14,1. Так как фактическое значение критерия меньше табличного, можно сделать вывод, что расхождения между эмпирическими и теоретическими частотами являются случайными.

Представим полученные результаты в графическом виде (рис. 5.5).

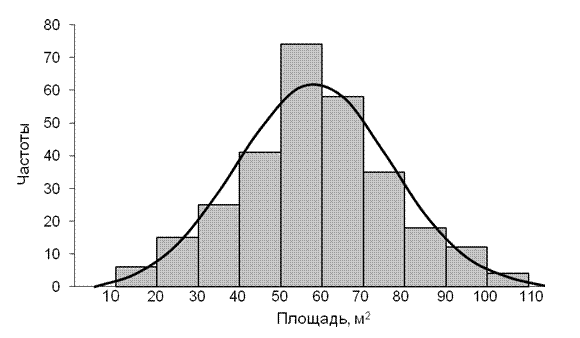
Рис. 5.5. Гистограмма распределения семей по общей площади их жилья
и аппроксимирующая ее кривая нормального распределения

При анализе материалов наблюдений можно использовать следующие свойства нормального распределения:

– вероятность того, что некоторое значение ряда больше или меньше  на , составляет 15,9 %;

– вероятность того, что некоторое значение ряда больше или меньше  на , составляет 2,3 %;

– вероятность того, что некоторое значение ряда больше или меньше  на , составляет 0,135 %.

Для рассматриваемого примера можно сделать следующие выводы: вероятность того, что в генеральной совокупности имеются квартиры с площадью более 95,3 м2 (2,3 %), с площадью более 113,9 м2 – 0,135 %.

Исследование связей между явлениями [5, 6]. Изучение любого социального явления будет неполным, если не исследованы его связи с другими явлениями и процессами. В рамках статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, это позволяет выявить факторы (признаки), оказывающие основное влияние на изменения изучаемых явлений. Особенности рассматриваемых методов заключаются в том, что они не только дают возможность установить наличие связи и ее характер, но и позволяют выразить связь аналитически и получить ее количественные оценки.

Различают функциональные и корреляционные связи.

В случае функциональной зависимости каждому значению одного признака строго соответствует одно определенное значение другого признака. Подобные однозначные (функциональные) связи между признаками в социальной работе встречаются крайне редко. В основном в методах социальных исследований анализируются корреляционные связи, при которых одному значению признака соответствует множество значений другого признака.

Наиболее простым случаем корреляционной зависимости является парная корреляция, т. е. зависимость между двумя признаками (результативным и одним из факторных).

Основными задачами при изучении корреляционных зависимостей являются:

1) построение математической формулы (уравнения), которая выражала бы зависимость одного признака от другого;

2) измерение тесноты такой зависимости.

Решение первой задачи, т. е. определение формы связи с последующим отысканием параметров уравнения, называется нахождением уравнения связи (уравнения регрессии). Возможны различные виды связей: линейная и нелинейная (параболическая, гиперболическая, показательная и т. д.). Параметры уравнений регрессии для всех видов связей чаще всего определяют с помощью метода наименьших квадратов.

Теснота связи между двумя признаками в случае линейной зависимости между ними обычно оценивается линейным коэффициентом корреляции:

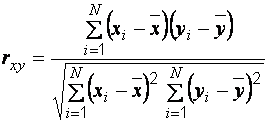,  (5.13)

где  – значения, принимаемые признаком ;  – значения, принимаемые признаком ;  – среднее арифметическое признака ;
 – среднее арифметическое признака ;  – количество членов рядов.

Величина коэффициента линейной корреляции может находиться только в интервале от минус 1 до плюс 1. Если коэффициент линейной корреляции по модулю оказывается близким к 1, это указывает на высокий уровень связи между анализируемыми признаками. Для интерпретации полученных связей большую роль играет знак коэффициента корреляции. При положительном значении коэффициента корреляции, приближающемся к единице, связь между признаками прямо пропорциональна: бóльшему значению одного признака соответствует бóльшее значение другого признака. В ситуации, когда коэффициент корреляции близок к значению минус 1, существует обратно пропорциональная зависимость: большему значению одного признака соответствует меньшее значение другого признака. В тех случаях, когда значение коэффициента корреляции равно минус 1 или плюс 1, связь между рассмотренными признаками является функциональной (обратной или прямой).

Проанализируем, имеются ли связи между численностью населения городов федерального округа и различными характеристиками безработицы в этих же городах (рис. 5.6, 5.7, 5.8, табл. 5.7).

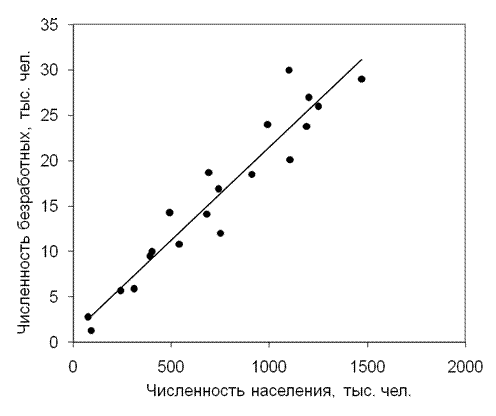
Рис. 5.6. Диаграмма рассеяния и линия регрессии численности
населения и безработных в городах федерального округа

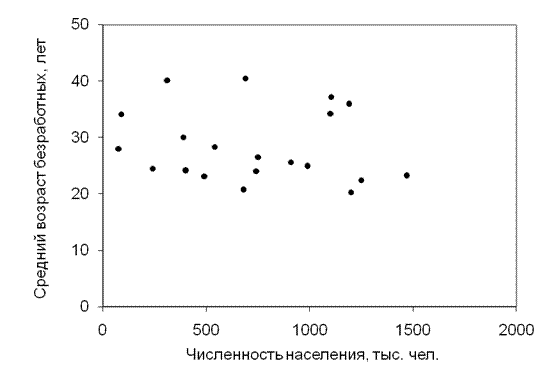
Рис. 5.7. Диаграмма рассеяния численности населения
и среднего возраста безработных в городах федерального округа

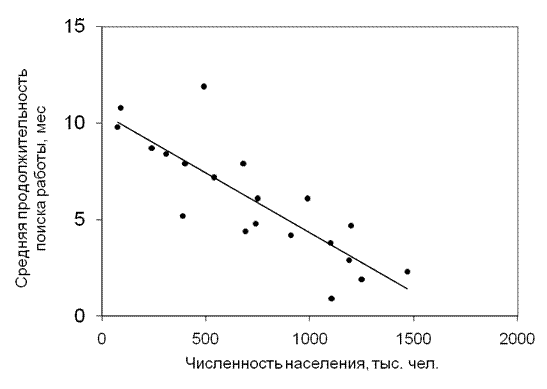
Рис. 5.8. Диаграмма рассеяния и линия регрессии численности
населения и средней продолжительности времени поиска работы

 безработными в городах федерального округа

Таблица 5.7

Численность населения и характеристика безработицы
в городах федерального округа

Построенная диаграмма рассеяния (рис. 5.8) свидетельствует, что между численностью населения городов и численностью безработных в этих городах существует (что вполне естественно) прямо пропорциональная связь (см. рис. 5.6). Коэффициент линейной корреляции между данными характеристиками составляет 0,957. Уравнение регрессии имеет вид:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5